Exercises B.7 Exercises
Drill yourself on multiplication table.
1.
Multiplication Facts
If you have not memorized the multiplication table yet, silently chant the multiplication table once or twice, and then do the following multiplication problems. If you need to look at a multiplication table, use Google to find one.
Do this problem every day until you are fluent with the multiplication table.
\(\displaystyle{8 \cdot 3}\) =
\(\displaystyle{9 \cdot 9}\) =
\(\displaystyle{4 \cdot 2}\) =
\(\displaystyle{8 \cdot 9}\) =
\(\displaystyle{5 \cdot 6}\) =
\(\displaystyle{3 \cdot 6}\) =
\(\displaystyle{2 \cdot 8}\) =
\(\displaystyle{3 \cdot 7}\) =
\(\displaystyle{7 \cdot 9}\) =
\(\displaystyle{2 \cdot 3}\) =
2.
Multiplication Facts
If you have not memorized the multiplication table yet, silently chant the multiplication table once or twice, and then do the following multiplication problems. If you need to look at a multiplication table, use Google to find one.
Do this problem every day until you are fluent with the multiplication table.
\(\displaystyle{2 \cdot 5}\) =
\(\displaystyle{6 \cdot 7}\) =
\(\displaystyle{8 \cdot 8}\) =
\(\displaystyle{5 \cdot 3}\) =
\(\displaystyle{4 \cdot 7}\) =
\(\displaystyle{9 \cdot 2}\) =
\(\displaystyle{4 \cdot 11}\) =
\(\displaystyle{5 \cdot 12}\) =
\(\displaystyle{2 \cdot 3}\) =
\(\displaystyle{4 \cdot 5}\) =
3.
Division Facts
Use multiplication facts reversely to do the following division problems. For example, since \(7 \cdot 8 = 56\text{,}\) we know \(56 \div 7 = 8\text{.}\)
Do this problem every day until you are fluent with doing this type of problem.
\(\displaystyle{45 \div 5}\) =
\(\displaystyle{32 \div 4}\) =
\(\displaystyle{12 \div 6}\) =
\(\displaystyle{54 \div 9}\) =
\(\displaystyle{14 \div 2}\) =
\(\displaystyle{40 \div 5}\) =
\(\displaystyle{18 \div 9}\) =
\(\displaystyle{36 \div 6}\) =
\(\displaystyle{48 \div 6}\) =
\(\displaystyle{6 \div 3}\) =
4.
Division Facts
Use multiplication facts reversely to do the following division problems. For example, since \(7 \cdot 8 = 56\text{,}\) we know \(56 \div 7 = 8\text{.}\)
Do this problem every day until you are fluent with doing this type of problem.
\(\displaystyle{90 \div 9}\) =
\(\displaystyle{99 \div 11}\) =
\(\displaystyle{56 \div 7}\) =
\(\displaystyle{84 \div 7}\) =
\(\displaystyle{50 \div 10}\) =
\(\displaystyle{60 \div 6}\) =
\(\displaystyle{8 \div 2}\) =
\(\displaystyle{15 \div 3}\) =
\(\displaystyle{77 \div 11}\) =
\(\displaystyle{30 \div 6}\) =
These skills practice exercises simply ask you to calculate something.
5.
Do the following additions without using a calculator.
\(\displaystyle{42 + 3 =}\)
\(\displaystyle{25 + 9 =}\)
\(\displaystyle{63 + 11 =}\)
\(\displaystyle{29 + 45 =}\)
6.
Do the following additions without using a calculator.
| 755 | 783 |
| \(+\;\)100 | \(+\;\)777 |
7.
Do the following subtraction without using a calculator.
\(\displaystyle{47 - 6 =}\)
\(\displaystyle{43 - 8 =}\)
\(\displaystyle{50 - 1 =}\)
8.
Do the following additions without using a calculator.
| 945 | 700 | 655 |
| \(-\;\)521 | \(-\;\)198 | \(-\;\)395 |
9.
Add these two decimals without using a calculator.
\(\displaystyle{9.58 + 34.6 =}\)
10.
Add these two decimals without using a calculator.
\(\displaystyle{1.002 + 29.51 =}\)
11.
Subtract these two decimals without using a calculator.
\(\displaystyle{5.8 - 3.65 =}\)
12.
Add these two decimals without using a calculator.
\(\displaystyle{35 + 1.45 =}\)
13.
Subtract these two decimals without using a calculator.
\(\displaystyle{41 - 5.14 =}\)
14.
Calculate without using a calculator. Don’t use commas in your answer.
\(6 \cdot 10\) =
\(6 \cdot 100\) =
\(6 \cdot 1000\) =
15.
Calculate without using a calculator. Don’t use commas in your answer.
\(53 \cdot 1000\) =
\(53 \cdot 10000\) =
\(53 \cdot 100000\) =
16.
Calculate without using a calculator. Don’t use commas in your answer.
\(7.17 \cdot 10\) =
\(7.17 \cdot 100\) =
\(7.17 \cdot 1000\) =
17.
Calculate without using a calculator. Don’t use commas in your answer.
\(84.782 \cdot 10\) =
\(84.782 \cdot 100000\) =
18.
Calculate without using a calculator. Don’t use commas in your answer.
\(49000000 \div 10\) =
\(49000000 \div 100\) =
\(49000000 \div 1000\) =
19.
Calculate without using a calculator.
\(1 \div 10\) =
\(1 \div 100\) =
\(1 \div 1000\) =
20.
Calculate without using a calculator.
\(27 \div 10\) =
\(27 \div 100\) =
\(27 \div 1000\) =
21.
Calculate without using a calculator.
\(36.45 \div 10\) =
\(36.45 \div 100\) =
\(36.45 \div 1000\) =
22.
Calculate without using a calculator.
\(4 \cdot 0.1\) =
\(4 \cdot 0.01\) =
\(4 \cdot 0.001\) =
23.
Calculate without using a calculator.
\(57 \cdot 0.1\) =
\(57 \cdot 0.01\) =
\(57 \cdot 0.001\) =
24.
Calculate without using a calculator.
\(64.01 \cdot 0.1\) =
\(64.01 \cdot 0.01\) =
\(64.01 \cdot 0.001\) =
25.
Calculate without using a calculator.
\(7 \div 0.1\) =
\(7 \div 0.01\) =
\(7 \div 0.001\) =
26.
Calculate without using a calculator.
\(86.85 \div 0.1\) =
\(86.85 \div 0.01\) =
\(86.85 \div 0.001\) =
27.
Calculate the following without using a calculator:
\(\displaystyle{9 \cdot 40 =}\)
\(\displaystyle{9 \cdot 400 =}\)
\(\displaystyle{9 \cdot 4000 =}\)
28.
Calculate the following without using a calculator:
\(\displaystyle{20 \cdot 9000 =}\)
\(\displaystyle{2000 \cdot 90 =}\)
\(\displaystyle{20 \cdot 9000 =}\)
29.
Calculate the following without using a calculator:
\(\displaystyle{3 \cdot 0.6 =}\)
\(\displaystyle{3 \cdot 0.06 =}\)
\(\displaystyle{3 \cdot 0.006 =}\)
30.
Calculate the following without using a calculator:
\(\displaystyle{0.4 \cdot 0.4 =}\)
\(\displaystyle{4 \cdot 0.004 =}\)
\(\displaystyle{0.04 \cdot 0.4 =}\)
31.
Calculate the following without using a calculator:
\(\displaystyle{0.09 \cdot 4000 =}\)
\(\displaystyle{0.009 \cdot 400 =}\)
\(\displaystyle{0.9 \cdot 40 =}\)
32.
It’s given that \(56\cdot48=2688\text{.}\) Calculate the following without using a calculator.
\(56 \cdot 480\) =
\(560 \cdot 48\) =
\(5600 \cdot 4800\) =
33.
It’s give that \(62\cdot86=5332\text{.}\) Use this fact to calculate the following without using a calculator:
\(\displaystyle{6.2 \cdot 0.86 =}\)
34.
It’s give that \(78\cdot23=1794\text{.}\) Use this fact to calculate the following without using a calculator:
\(\displaystyle{7.8 (-2.3) =}\)
35.
It’s give that \(85\cdot61=5185\text{.}\) Use this fact to calculate the following without using a calculator:
\(\displaystyle{(-8.5)(-0.61) =}\)
36.
It’s given that \(92\cdot17=1564\text{.}\) Calculate the following without using a calculator.
\(92 \cdot 1.7\) =
\(9.2 \cdot 17\) =
\(9.2 \cdot 0.17\) =
37.
It’s given that \(185\cdot52=9620\text{.}\) Calculate the following without using a calculator.
\(1.85 \cdot 0.52\) =
\(0.185 \cdot 5.2\) =
\(18.5 \cdot 5.2\) =
38.
It’s given that \(25\cdot82=2050\text{.}\) Calculate the following without using a calculator.
\(2.5 \cdot 820\) =
\(2500 \cdot 8.2\) =
\(0.25 \cdot 8200\) =
39.
Evaluate the following expressions that have integer exponents:
\(\displaystyle{3^{2}=}\)
\(\displaystyle{2^{3}=}\)
40.
Evaluate the following expressions that have integer exponents:
\(\displaystyle{1^{14}=}\)
\(\displaystyle{0^{38}=}\)
\(\displaystyle{16^{1}=}\)
41.
Evaluate the following expressions. If the answer is undefined, type DNE (meaning “does not exist”).
\(\displaystyle{\frac{0}{6} =}\)
\(\displaystyle{\frac{6}{0} =}\)
42.
Do the following division problems without using a calculator.
\(\displaystyle{12000 \div 6 =}\)
\(\displaystyle{400000 \div 20000 =}\)
43.
Do the following multiplication problems without using a calculator.
\(\displaystyle{70000 \cdot 70000 =}\)
\(\displaystyle{70 \cdot 700 =}\)
Apply your skills with arithmetic to solve some applied questions.
44.
Amber is gambling. She won \({\$27.00}\) in the first game, lost \({\$13.00}\) in the second game, and won \({\$17.00}\) in the third game. Altogether, how much money did she win?
Altogether, Amber won .
45.
Aleric is working to pass a local measure, and he needs to collect a total of \(101\) signatures in three days. On the first day, he collected \(48\) signatures; on the second day, he collected \(11\text{.}\) To complete her job, how many more signatures does he need to collect on the third day?
Solution: Aleric needs to collect more signatures on the third day.
46.
Sharell collects Pokemon cards. This table records the number of cards she collected last year:
| Months | Number of cards collected |
| January | 19 |
| February | 48 |
| March | 26 |
| April | 48 |
| May | 24 |
| June | 25 |
| July | 14 |
| August | 13 |
| September | 35 |
| October | 27 |
| November | 35 |
| December | 16 |
Answer the following questions:
In the first quarter (January, February and March), how many Pokemon cards did Sharell collect in all?
In the first half of the year, how many more cards did Sharell collect than in the second half?
47.
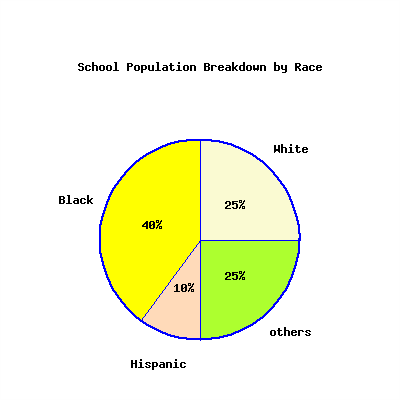
The pie chart represents a school’s student population. Fill in the blank.
The school’s white, black and Hispanic students, altogether, have \(\%\) more students than students of other races.
48.
The following bar graph shows the distance different runners ran in a relay race.
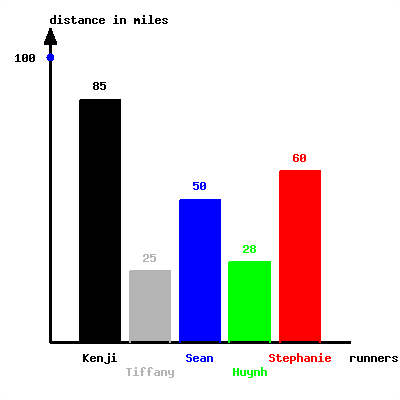
Identify those two runners who ran the longest distances, and then identify those two runners who ran the shortest distances.
The best two runners ran more miles than the worst two runners.
49.
This line graph shows a club’s membership change over a few months.
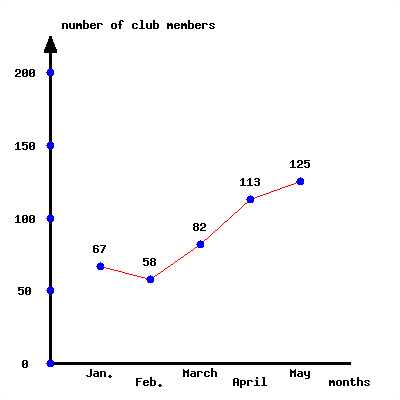
From Jan. to May, what is the club’s membership change?
Solution: From Jan. to May, the club’s membership change was .
50.
If \(1\) dollar is represented by the integer \(1\text{,}\) write the following money amount with decimals. There is no need to type the dollar sign.
\(5 \text{ dimes} =\)
\(5 \text{ dollars} =\)
\(5 \text{ cents} =\)
51.
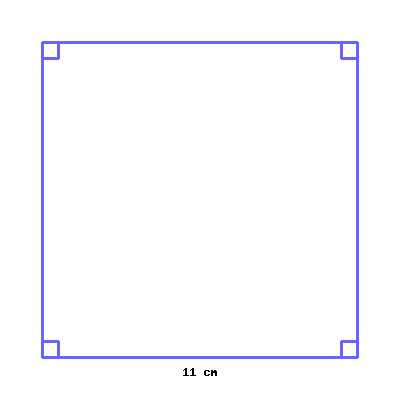
Its perimeter is and its area is .
(Use cm for centimeters and cm^2 for square centimeters.)
52.
In a class, the teacher handed out \(11\) marbles to each of his \(17\) students. How many marbles did the teacher hand out altogether?
The teacher handed out a total of marbles.
53.
Kayla is saving money to purchase \(35\) Lego figures. Each Lego figure costs \({\$7.48}\text{.}\) How much money does she need to save?
Kayla needs to save .
54.
Jessica is saving money to buy action figures. She plans to buy \(14\) Smurf action figures, each of which costs \({\$4.19}\text{.}\) In addition, she also plans to buy \(20\) SpongeBob action figures, each of which costs \({\$2.45}\text{.}\)
How much money does Jessica need to save?
Jessica needs to save .
55.
dMarie loves sports. Every week, she practices \(40\) minutes of basketball, \(60\) minutes of volleyball, and \(85\) minutes of soccer.
In total, how many minutes of soccer will dMarie play in \(12\) weeks?
Solution: dMarie will play minutes of soccer in \(12\) weeks.
56.
Connor and Gosheven are participating in a summer reading program. Connor reads \(42\) pages every day, and Gosheven reads \(12\) more pages than Connor every day.
How many pages will Gosheven read in \(54\) days?
Solution: Gosheven will read pages in \(54\) days.
57.
Morah and Evan are participating in a summer reading program. Morah reads \(44\) pages every day, and Evan reads \(8\) more pages than Morah every day.
How many more pages will Evan read than Morah in \(36\) days?
Solution: Evan will read more pages than Morah in \(36\) days.
58.
A queen termite produces \(7\) eggs every minute. How many eggs does the queen produce every week?
Solution: The queen termite produces eggs every week.
59.
Michael plays in his school’s basketball team. Last season, Michael scored an average of \(18\) points per game. The season had a total of \(50\) games, but Michael missed \(8\) games. How many points did Michael score in total last season?
Solution: Michael scored a total of points last season.
60.
A city holds a walking competition 5 times per month. The competition covers \({5.8\ {\rm km}}\) (kilometers). Nenia completed each event in the past \(7\) years. How many total kilometers did Nenia walk in this event in the past \(7\) years?
Solution: Nenia walked a total of in this event in the past \(7\) years.
Use km for kilometers.
61.
In a class, the teacher will hand out a total of \(416\) marbles to all his \(26\) students evenly. How many marbles will each student receive?
Solution: Each student will receive marbles.
62.
For an activity in a class, each student will use \(12\) marbles. The teacher purchased a total of \(336\) marbles for his class. How many students are there in this class?
Solution: There are students in this class.
63.
Rita saved \({\$300.00}\text{,}\) and will start spending her money on Lego figures. Each week, Rita will spend \({\$15.00}\) to buy a Lego figure. In how many weeks will Rita have spent all her money?
Solution: Rita will have spent all her money in weeks.
64.
Kristen just bought a total of \(82\) movies. He will watch \(2\) movies every week. In how many weeks will Kristen finish watching all the movies?
Solution: Kristen will finish watching all movies in weeks.
65.
Dave drove a total of \({216\ {\rm mi}}\) in \({6\ {\rm hr}}\text{.}\) What was Dave’s speed in miles per hour?
Solution: Dave drove at the speed of .
Use mi for miles, hr for hours, and mi/hr for miles per hour.
66.
Tiffany drove \({492\ {\rm mi}}\) at a constant speed of \({41\ {\textstyle\frac{\rm\mathstrut mi}{\rm\mathstrut hr}}}\text{.}\) How many hours did Tiffany drive? In your answer, use mi for miles, hr for hours, and mi/hr for miles per hour.
Tiffany drove for .
67.
A tank can drain \({1368\ {\rm L}}\) (liters) of water in \({36\ {\rm min}}\) minutes. How many liters of water does the tank drain per minute?
Solution: The tank drains water at the rate of .
Use L for liters, min for minutes, and L/min for liters per minute.
68.
A tank drains \(40\) liters of water per minute. How many minutes does it take to drain \({1000\ {\rm L}}\) (liters) of water?
Solution: It takes to drain \({1000\ {\rm L}}\) of water.
Use L for liters, min for minutes, and L/min for liters per minute.
69.
A queen termite produces \(60480\) eggs every week. How many eggs does the queen produce every minute?
Solution: The queen termite produces eggs every minute.
70.
Samantha is a star player in her basketball team. Last season, Samantha scored a total of \(848\) points in the whole season. The season had a total of \(60\) games, but Samantha missed \(7\) games. On average, how many points did Samantha score in each game?
Solution: On average, Samantha scored points in each game.
71.
A team is climbing a mountain, which is \(5920\) meters high. The team plans to climb \(185\) meters every day. How many days would it take the team to climb to the top?
Solution: It would take the team days to climb to the top.
72.
An archeology team is studying a buried city. The team can cover \(49\) square meters every day. The whole area covers about \(2548\) square meters. How many days will it take the team to complete studying the whole area?
Solution: It would take the team days to cover the whole area.
73.
One piece of paper is approximately \(5\) millimeters in thickness. A stack of paper is \(2165\) millimeters tall. About how many pieces of paper are there in the stack?
Solution: There are about pieces of paper in the stack.
74.
In a class, the teacher will hand out \(275\) marbles to all his \(17\) students evenly. How many marbles will each student receive? How many marbles will be left over?
Solution:
Each student will receive marbles.
There will be left-over marbles.
75.
A teacher is doing an activity in a class with \(26\) students. The teacher had a total of \(474\) marbles, and handed them out evenly among all students until not enough marbles are left for another round. Some marbles were left over, and the teacher divided those left-over marbles evenly into \(2\) piles.
How many marbles are in each pile?
Solution: There are marbles in each pile.
76.
Devon saved \({\$88.00}\text{,}\) and will start spending his money on Lego figures. Each week, Devon will spend \({\$7.00}\) to buy a Lego figure. For how many weeks can Devon spend his money this way? How much left-over money will he have?
Solution:
Devon can spend his money this way for weeks.
There will be of left-over money.
77.
Devon saved \({\$88.00}\text{,}\) and will purchase some Lego figures. Each Lego figure costs \({\$7.00}\text{.}\) How many Lego figures can Devon afford?
Solution: Devon can afford Lego figures.
78.
A school is planning for a field trip for \(733\) students and staff. Each school bus can hold \(49\) people. How many school buses are needed?
Solution: school buses are needed.
