Section 1.7 Comparison Symbols and Notation for Intervals
As you know, \(8\) is larger than \(3\text{;}\) that's a specific comparison between two numbers. We can also make a comparison between two less specific numbers, like if we say that average rent in Portland in 2016 is larger than it was in 2009. That makes a comparison using unspecified amounts. This section will go over the mathematical shorthand notation for making these kinds of comparisons.
In Oregon, only people who are \(18\) years old or older can vote in statewide elections. 1 Does that seem like a statement about the number \(18\text{?}\) Maybe. But it's also a statement about numbers like \(37\) and \(62\text{:}\) it says that people of these ages may vote as well. This section will also get into the mathematical notation for large collections of numbers like this.
Subsection 1.7.1 Comparison Symbols
In everyday language you can say something like “\(8\) is larger than \(3\text{.}\)” In mathematical writing, it's not convenient to write that out in English. Instead the symbol “\(\gt\)” has been adopted, and it's used like this:
and read out loud as “\(8\) is greater than \(3\text{.}\)” The symbol “\(\gt\)” is called the greater-than symbol.
Checkpoint 1.7.1.
Remark 1.7.2.
At some point in history, someone felt that \(\gt\) was a good symbol for “is greater than.” In “\(8\gt3\text{,}\)” the tall side of the symbol is with the larger of the two numbers, and the small pointed side is with the smaller of the two numbers.
We have to be careful when negative numbers are part of the comparison though. Is \(-8\) larger or smaller than \(-3\text{?}\) In some sense \(-8\) is larger, because if you owe someone \(8\) dollars, that's more than owing them \(3\) dollars. But that is not how the \(\gt\) symbol works. This symbol is meant to tell you which number is farther to the right on a number line. And if that's how it goes, then \(-3\gt-8\text{.}\)
Checkpoint 1.7.4.
Checkpoint 1.7.5.
The greater-than symbol has a close relative, the greater-than-or-equal-to symbol, “\(\geq\text{.}\)” It means just like it sounds: the first number is either greater than, or equal to, the second number. These are all true statements:
but one of these three statements is false:
Remark 1.7.6.
While it may not be that useful that we can write \(3\geq3\text{,}\) this symbol is quite useful when specific numbers aren't explicitly used on at least one side, like in these examples:
Sometimes you want to emphasize that one number is less than another number instead of emphasizing which number is greater. To do this, we have symbols that are reversed from \(\gt\) and \(\geq\text{.}\) The symbol “\(\lt\)” is the less-than symbol and it's used like this:
and read out loud as “\(3\) is less than \(8\text{.}\)”
Table 1.7.7 gives the complete list of all six comparison symbols. Note that we've only discussed three in this section so far, but you already know the equals symbol and have likely also seen the symbol “\(\neq\text{,}\)” which means “not equal to.”
| Symbol | Means | Examples | ||
| \(=\) | equals | \(13=13\qquad\) | \(\frac{5}{4}=1.25\) | \(5\stackrel{\text{no}}{=}6\) |
| \(\gt\) | is greater than | \(13\gt11\) | \(\pi\gt3\) | \(9\stackrel{\text{no}}{\gt}9\) |
| \(\geq\) | is greater than or equal to | \(13\geq11\) | \(3\geq3\) | \(11.2\stackrel{\text{no}}{\geq}10.2\) |
| \(\lt\) | is less than | \(-3\lt8\) | \(\frac{1}{2}\lt\frac{2}{3}\) | \(2\stackrel{\text{no}}{\lt}-2\) |
| \(\leq\) | is less than or equal to | \(-3\leq8\) | \(3\leq3\) | \(\frac{4}{5}\stackrel{\text{no}}{\leq}\frac{3}{5}\) |
| \(\neq\) | is not equal to | \(10\neq20\) | \(\frac{1}{2}\neq1.2\) | \(\frac{3}{8}\stackrel{\text{no}}{\neq}0.375\) |
Subsection 1.7.2 Set-Builder and Interval Notation
If you say
and have a particular voter in mind, what is that person's age? There's no way to know for sure. Maybe they are \(18\text{,}\) but maybe they are older. When we want to represent an unknown or changing numerical quantity, we use a variable to do so. For example, it's helpful to use a variable, in this case the letter \(a\text{,}\) to represent age (in years) and then to visualize the possibilities with a number line, as in Figure 1.7.8.
The shaded portion of the number line in Figure 1.7.8 is a mathematical interval. For now, that just means a collection of certain numbers. In this case, it's all the numbers \(18\) and above.
The number line in Figure 1.7.8 is a graphical representation of a collection of certain numbers. We have two notations, set-builder notation and interval notation, that we also use to represent such collections of numbers.
Definition 1.7.9. Set-Builder Notation.
Set-builder notation attempts to directly say the condition that numbers in the interval satisfy, where a variable, usually \(x\) is used to represent an arbitrary number in the interval. In general, we write set-builder notation like:
and read it out loud as “the set of all \(x\) such that ….” For example,
is read out loud as “the set of all \(x\) such that \(x\) is greater than or equal to \(18\text{.}\)” The breakdown is as follows.
| \(\highlight{\{}\lowlight{x\mid x\geq18}\highlight{\}}\) | the set of |
| \(\lowlight{\{}\highlight{x}\lowlight{{}\mid x\geq18\}}\) | all \(x\) |
| \(\lowlight{\{x}\highlight{{}\mid{}}\lowlight{x\geq18\}}\) | such that |
| \(\lowlight{\{x\mid{}}\highlight{x\geq18}\lowlight{\}}\) | \(x\) is greater than or equal to \(18\) |
Definition 1.7.10. Interval Notation.
Interval notation represents a collection of numbers by only stating where the collection starts and stops, using parentheses and square brackets to show if the end values are included (or not). For example, in Figure 1.7.8, the interval starts at \(18\text{.}\) To the right, the interval extends forever and has no end, so we use the \(\infty\) symbol (meaning "infinity"). This particular interval is denoted:
Why use “\([\)” on one side and “\()\)” on the other? The square bracket tells us that \(18\) is part of the interval and the round parenthesis tells us that \(\infty\) is not part of the interval. 2
In general there are four types of infinite intervals. Take note of the different uses of round parentheses and square brackets.
Checkpoint 1.7.15. Interval and Set-Builder Notation from Number Lines.
Exercises 1.7.3 Exercises
Review and Warmup
1.
Write the decimal number as a fraction.
\(0.45\) =
2.
Write the decimal number as a fraction.
\(0.55\) =
3.
Write the decimal number as a fraction.
\(6.35\) =
4.
Write the decimal number as a fraction.
\(7.85\) =
5.
Write the decimal number as a fraction.
\(0.852\) =
6.
Write the decimal number as a fraction.
\(0.916\) =
7.
Write the fraction as a decimal number.
\({{\frac{3}{4}}}\) =
\({{\frac{11}{25}}}\) =
8.
Write the fraction as a decimal number.
\({{\frac{1}{4}}}\) =
\({{\frac{7}{8}}}\) =
9.
Write the mixed number as a decimal number.
\({8 {\textstyle\frac{4}{5}}}\) =
\({1 {\textstyle\frac{3}{4}}}\) =
10.
Write the mixed number as a decimal number.
\({6 {\textstyle\frac{5}{8}}}\) =
\({6 {\textstyle\frac{17}{20}}}\) =
Ordering Numbers
11.
Use the \(\gt\) symbol to arrange the following numbers in order from greatest to least. For example, your answer might look like 4>3>2>1>0.
12.
Use the \(\gt\) symbol to arrange the following numbers in order from greatest to least. For example, your answer might look like 4>3>2>1>0.
13.
Use the \(\gt\) symbol to arrange the following numbers in order from greatest to least. For example, your answer might look like 4>3>2>1>0.
14.
Use the \(\gt\) symbol to arrange the following numbers in order from greatest to least. For example, your answer might look like 4>3>2>1>0.
15.
Use the \(\gt\) symbol to arrange the following numbers in order from greatest to least. For example, your answer might look like 4>3>2>1>0.
16.
Use the \(\gt\) symbol to arrange the following numbers in order from greatest to least. For example, your answer might look like 4>3>2>1>0.
17.
Use the \(\gt\) symbol to arrange the following numbers in order from greatest to least. For example, your answer might look like 4>3>2>1>0.
18.
Use the \(\gt\) symbol to arrange the following numbers in order from greatest to least. For example, your answer might look like 4>3>2>1>0.
True/False
19.
Decide if each comparison is true or false.
\(-9\lt-9\)
True
False
\(3\gt3\)
True
False
\(9\geq9\)
True
False
\(-1\gt-2\)
True
False
\(3\leq2\)
True
False
\(6\geq1\)
True
False
20.
Decide if each comparison is true or false.
\(-1\geq2\)
True
False
\(1\neq6\)
True
False
\(1\neq1\)
True
False
\(4\leq4\)
True
False
\(-3\geq-3\)
True
False
\(-1=-1\)
True
False
21.
Decide if each comparison is true or false.
\({\frac{5}{6}}\geq{\frac{5}{6}}\)
True
False
\({\frac{17}{8}}\geq{\frac{25}{3}}\)
True
False
\({\frac{9}{4}}\gt{\frac{9}{4}}\)
True
False
\(-{\frac{41}{5}}\gt{\frac{9}{2}}\)
True
False
\({\frac{3}{5}}\leq{\frac{9}{15}}\)
True
False
\(-{\frac{57}{9}}\lt-{\frac{27}{7}}\)
True
False
22.
Decide if each comparison is true or false.
\(-{\frac{5}{5}}\lt-{\frac{10}{10}}\)
True
False
\(-{\frac{7}{6}}\geq-{\frac{21}{18}}\)
True
False
\(-{\frac{49}{9}}\neq-{\frac{10}{7}}\)
True
False
\({\frac{1}{8}}\gt{\frac{2}{16}}\)
True
False
\(-{\frac{52}{9}}\lt-{\frac{22}{4}}\)
True
False
\({\frac{84}{9}}={\frac{33}{8}}\)
True
False
Comparisons
23.
Choose \(\lt \text{,}\) \(>\text{,}\) or \(=\) to make a true statement.
\(\displaystyle{-\frac{2}{7}}\)
<
>
=
24.
Choose \(\lt \text{,}\) \(>\text{,}\) or \(=\) to make a true statement.
\(\displaystyle{-\frac{1}{9}}\)
<
>
=
25.
Choose \(\lt \text{,}\) \(>\text{,}\) or \(=\) to make a true statement.
\({{\frac{1}{4}}} + {{\frac{3}{2}}}\)
<
>
=
26.
Choose \(\lt \text{,}\) \(>\text{,}\) or \(=\) to make a true statement.
\({{\frac{1}{2}}} + {{\frac{5}{4}}}\)
<
>
=
27.
Choose \(\lt \text{,}\) \(>\text{,}\) or \(=\) to make a true statement.
\({{\frac{5}{17}}} \div {{\frac{5}{17}}}\)
<
>
=
28.
Choose \(\lt \text{,}\) \(>\text{,}\) or \(=\) to make a true statement.
\({{\frac{8}{11}}} \div {{\frac{8}{11}}}\)
<
>
=
29.
Choose \(\lt \text{,}\) \(>\text{,}\) or \(=\) to make a true statement.
\(\displaystyle{{-5 {\textstyle\frac{1}{2}}}}\)
<
>
=
30.
Choose \(\lt \text{,}\) \(>\text{,}\) or \(=\) to make a true statement.
\(\displaystyle{{-4 {\textstyle\frac{1}{3}}}}\)
<
>
=
31.
Choose \(\lt \text{,}\) \(>\text{,}\) or \(=\) to make a true statement.
\(\displaystyle{{-8 {\textstyle\frac{1}{2}}}}\)
<
>
=
32.
Choose \(\lt \text{,}\) \(>\text{,}\) or \(=\) to make a true statement.
\(\displaystyle{{-9 {\textstyle\frac{1}{2}}}}\)
<
>
=
33.
Choose \(\lt \text{,}\) \(>\text{,}\) or \(=\) to make a true statement.
\(\displaystyle{ \left\lvert {-{\frac{11}{20}}} \right\rvert }\)
<
>
=
34.
Choose \(\lt \text{,}\) \(>\text{,}\) or \(=\) to make a true statement.
\(\displaystyle{ \left\lvert {-{\frac{3}{4}}} \right\rvert }\)
<
>
=
Set-builder and Interval Notation
35.
For the interval expressed in the number line, write it using set-builder notation and interval notation.
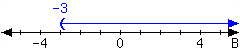
In set-builder notation:
In interval notation:
36.
For the interval expressed in the number line, write it using set-builder notation and interval notation.
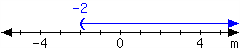
In set-builder notation:
In interval notation:
37.
For the interval expressed in the number line, write it using set-builder notation and interval notation.
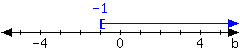
In set-builder notation:
In interval notation:
38.
For the interval expressed in the number line, write it using set-builder notation and interval notation.
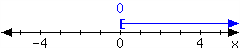
In set-builder notation:
In interval notation:
39.
For the interval expressed in the number line, write it using set-builder notation and interval notation.
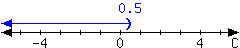
In set-builder notation:
In interval notation:
40.
For the interval expressed in the number line, write it using set-builder notation and interval notation.
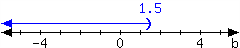
In set-builder notation:
In interval notation:
41.
For the interval expressed in the number line, write it using set-builder notation and interval notation.
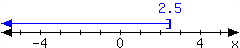
In set-builder notation:
In interval notation:
42.
For the interval expressed in the number line, write it using set-builder notation and interval notation.
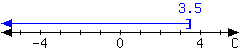
In set-builder notation:
In interval notation:
Convert to Interval Notation
43.
A set is written using set-builder notation. Write it using interval notation.
\(\displaystyle{ \{ x \mid {{x}} \leq -10 \} }\)
44.
A set is written using set-builder notation. Write it using interval notation.
\(\displaystyle{ \{ x \mid {{x}} \leq -8 \} }\)
45.
A set is written using set-builder notation. Write it using interval notation.
\(\displaystyle{ \{ x \mid {{x}} \geq -5 \} }\)
46.
A set is written using set-builder notation. Write it using interval notation.
\(\displaystyle{ \{ x \mid {{x}} \geq -3 \} }\)
47.
A set is written using set-builder notation. Write it using interval notation.
\(\displaystyle{ \{ x \mid{{x}} \lt -1 \} }\)
48.
A set is written using set-builder notation. Write it using interval notation.
\(\displaystyle{ \{ x \mid{{x}} \lt 2 \} }\)
49.
A set is written using set-builder notation. Write it using interval notation.
\(\displaystyle{ \{ x \mid {{x}} \gt 4 \} }\)
50.
A set is written using set-builder notation. Write it using interval notation.
\(\displaystyle{ \{ x \mid {{x}} \gt 6 \} }\)
51.
A set is written using set-builder notation. Write it using interval notation.
\(\displaystyle{ \{ x \mid {9} \gt {x} \} }\)
52.
A set is written using set-builder notation. Write it using interval notation.
\(\displaystyle{ \{ x \mid {-10} \gt {x} \} }\)
53.
A set is written using set-builder notation. Write it using interval notation.
\(\displaystyle{ \{ x \mid {-8} \geq {x} \} }\)
54.
A set is written using set-builder notation. Write it using interval notation.
\(\displaystyle{ \{ x \mid {-5} \geq {x} \} }\)
55.
A set is written using set-builder notation. Write it using interval notation.
\(\displaystyle{ \{ x\mid{-3} \leq {x} \} }\)
56.
A set is written using set-builder notation. Write it using interval notation.
\(\displaystyle{ \{ x\mid{-1} \leq {x} \} }\)
57.
A set is written using set-builder notation. Write it using interval notation.
\(\displaystyle{ \{ x \mid {2} \lt {x} \} }\)
58.
A set is written using set-builder notation. Write it using interval notation.
\(\displaystyle{ \{ x \mid {4} \lt {x} \} }\)
59.
A set is written using set-builder notation. Write it using interval notation.
\(\displaystyle{ \left\{ x \mid {{{\frac{9}{8}}}} \lt {x} \right\} }\)
60.
A set is written using set-builder notation. Write it using interval notation.
\(\displaystyle{ \left\{ x \mid {{{\frac{10}{3}}}} \lt {x} \right\} }\)
61.
A set is written using set-builder notation. Write it using interval notation.
\(\displaystyle{ \left\{ x \mid {{x}} \leq {-{\frac{1}{2}}} \right\} }\)
62.
A set is written using set-builder notation. Write it using interval notation.
\(\displaystyle{ \left\{ x \mid {{x}} \leq {-{\frac{2}{9}}} \right\} }\)
63.
A set is written using set-builder notation. Write it using interval notation.
\(\displaystyle{ \{ x \mid {x} \leq 0 \} }\)
64.
A set is written using set-builder notation. Write it using interval notation.
\(\displaystyle{ \{ x \mid 0 \lt {x} \} }\)
