Skip to main content

Section 1.8 Basic Math Chapter Review

Subsection 1.8.1 Arithmetic with Negative Numbers

Adding Real Numbers with the Same Sign.

When adding two numbers with the same sign, we can ignore the signs and simply add the numbers as if they were both positive.

Example 1.8.1.

  1. \(\displaystyle 5+2=7\)

  2. \(\displaystyle -5+(-2)=-7\)

Adding Real Numbers with Opposite Signs.

When adding two numbers with opposite signs, we find those two numbers' difference. The sum has the same sign as the number with the bigger value. If those two numbers have the same value, the sum is \(0\text{.}\)

Example 1.8.2.

  1. \(\displaystyle 5+(-2)=3\)

  2. \(\displaystyle (-5)+2=-3\)

Subtracting a Positive Number.

When subtracting a positive number, we can change the problem to adding the opposite number and then apply the methods of adding numbers.

Example 1.8.3.

  1. \(\displaystyle \begin{aligned}[t] 5-2\amp=5+(-2)\\ \amp=3 \end{aligned}\)

  2. \(\displaystyle \begin{aligned}[t] 2-5\amp=2+(-5)\\ \amp=-3 \end{aligned}\)

  3. \(\displaystyle \begin{aligned}[t] -5-2\amp=-5+(-2)\\ \amp=3 \end{aligned}\)

Subtracting a Negative Number.

When subtracting a negative number, we can change those two negative signs to a positive sign and then apply the methods of adding numbers.

Example 1.8.4.

  1. \(\displaystyle \begin{aligned}[t] 5-(-2)\amp=5+2\\ \amp=7 \end{aligned}\)

  2. \(\displaystyle \begin{aligned}[t] -5-(-2)\amp=-5+2\\ \amp=-3 \end{aligned}\)

  3. \(\displaystyle \begin{aligned}[t] -2-(-5)\amp=-2+5\\ \amp=3 \end{aligned}\)

Multiplication and Division of Real Numbers.

When multiplying and dividing real numbers, each pair of negative signs cancel out each other (becoming a positive sign). If there is still one negative sign left, the result is negative; otherwise the result is positive.

Example 1.8.5.

  1. \(\displaystyle (6)(-2)=-12\)

  2. \(\displaystyle (-6)(2)=-12\)

  3. \(\displaystyle (-6)(-2)=12\)

  4. \(\displaystyle (-6)(-2)(-1)=-12\)

  5. \(\displaystyle (-6)(-2)(-1)(-1)=12\)

  6. \(\displaystyle \frac{12}{-2}=-6\)

  7. \(\displaystyle \frac{-12}{2}=-6\)

  8. \(\displaystyle \frac{-12}{-2}=6\)

Powers.

When we raise a negative number to a certain power, apply the rules of multiplying real numbers: each pair of negative signs cancel out each other.

Example 1.8.6.

  1. \(\displaystyle \begin{aligned}[t] (-2)^2\amp=(-2)(-2)\\ \amp=4 \end{aligned}\)

  2. \(\displaystyle \begin{aligned}[t] (-2)^3\amp=(-2)(-2)(-2)\\ \amp=-8 \end{aligned}\)

  3. \(\displaystyle \begin{aligned}[t] (-2)^4\amp=(-2)(-2)(-2)(-2)\\ \amp=16 \end{aligned}\)

Difference between \((-a)^n\) and \(-a^n\).

For the exponent expression \(2^3\text{,}\) the number \(2\) is called the base and the number \(3\) is called the exponent. The base of \((-a)^n\) is \(-a\text{,}\) while the base of \(-a^n\) is \(a\text{.}\) This makes a difference in the result when the power is an even number.

Example 1.8.7.

  1. \(\displaystyle \begin{aligned}[t] (-4)^2\amp=(-4)(-4)\\ \amp=16 \end{aligned}\)

  2. \(\displaystyle \begin{aligned}[t] -4^2\amp=-(4)(4)\\ \amp=-16 \end{aligned}\)

  3. \(\displaystyle \begin{aligned}[t] (-4)^3\amp=(-4)(-4)(-4)\\ \amp=-64 \end{aligned}\)

  4. \(\displaystyle \begin{aligned}[t] -4^3\amp=-(4)(4)(4)\\ \amp=-64 \end{aligned}\)

Subsection 1.8.2 Fraction Arithmetic

Example 1.8.8. Multiplying Fractions.

When multiplying two fractions, we simply multiply the numerators and denominators. To avoid big numbers, we should reduce fractions before multiplying. If one number is an integer, we can write it as a fraction with a denominator of \(1\text{.}\) For example, \(2=\frac{2}{1}\text{.}\)

\begin{align*} \frac{1}{2}\cdot\frac{3}{4}\amp=\frac{1\cdot3}{2\cdot4}\\ \amp=\frac{3}{8} \end{align*}
Example 1.8.9. Dividing Fractions.

When dividing two fractions, we “flip” the second number and then do multiplication.

\begin{align*} \frac{1}{2}\div\frac{4}{3}\amp=\frac{1}{2}\cdot\frac{3}{4}\\ \amp=\frac{3}{8} \end{align*}
Example 1.8.10. Adding/Subtracting Fractions.

Before adding/subtracting fractions, we need to change each fraction's denominator to the same number, called the common denominator. Then, we add/subtract the numerators, and the denominator remains the same.

\begin{align*} \frac{1}{2}-\frac{1}{3}\amp=\frac{1}{2}\multiplyright{\frac{3}{3}}-\frac{1}{3}\multiplyright{\frac{2}{2}}\\ \amp=\frac{3}{6}-\frac{2}{6}\\ \amp=\frac{1}{6} \end{align*}

Subsection 1.8.3 Unit Analysis

Unit analysis is a particular process that uses unit ratios to convert units. You may refer to Appendix A to find unit conversion facts needed to do these conversions.

Example 1.8.11. Using Multiple Unit Ratios.

How many grams are in \(5\) pounds?

\begin{align*} 5\,\text{lb}\amp=\frac{5\,\text{lb}}{1}\amp\amp\text{Rewrite as a ratio.}\\ \amp=\frac{5\,\text{lb}}{1}\cdot\frac{1\,\text{kg}}{2.205\,\text{lb}}\cdot\frac{1000\,\text{g}}{1\,\text{kg}}\amp\amp\text{Two unit ratios are needed.}\\ \amp=\frac{5\,\firstcancel{\text{lb}}}{1}\cdot\frac{1\,\secondcancel{\text{kg}}}{2.205\,\firstcancel{\text{lb}}}\cdot\frac{1000\,\text{g}}{1\,\secondcancel{\text{kg}}}\amp\amp\text{Units may now cancel.}\\ \amp=\frac{5}{1}\cdot\frac{1}{2.205}\cdot\frac{1000\,\text{g}}{1}\amp\amp\text{Only units of g remain.}\\ \amp=\frac{5\cdot1000}{2.205}\,\text{g}\amp\amp\text{Multiply what's left and then divide.}\\ \amp\approx2268\,\text{g} \end{align*}

So \(5\) pounds is about \(2268\) grams.

Example 1.8.12. Converting Squared or Cubed Units.

Convert \(240\) square inches into square centimeters.

\begin{align*} 240\,\text{in}^2\amp=\frac{240\,\text{in}^2}{1}\amp\amp\text{Rewrite as a ratio.}\\ \amp=\frac{240\,\text{in}^2}{1}\cdot\left(\frac{2.54\,\text{cm}}{1\,\text{in}}\right)^2\amp\amp\text{The unit ratio needs to be squared.}\\ \amp=\frac{240\,\text{in}^2}{1}\cdot\frac{2.54^2\,\text{cm}^2}{1\,\text{in}^2}\amp\amp\text{Everything inside the parentheses is squared.}\\ \amp=\frac{240\,\cancel{\text{in}^2}}{1}\cdot\frac{2.54^2\,\text{cm}^2}{1\,\cancel{\text{in}^2}}\amp\amp\text{Units may now cancel.}\\ \amp=\frac{240}{1}\cdot\frac{2.54^2\,\text{cm}^2}{1}\amp\amp\text{Only units of sq cm remain.}\\ \amp=240\cdot2.54^2\,\text{cm}^2\amp\amp\text{Multiply.}\\ \amp\approx1548\,\text{cm}^2 \end{align*}

So \(240\) square inches is approximately \(1548\) square centimeters.

Example 1.8.13. Converting Rates.

Gold has a density of 19.3 g⁄mL. What is this density in ounces per cubic inch?

\begin{align*} 19.3\,\frac{\text{g}}{\text{mL}}\amp=\frac{19.3\,\text{g}}{1\,\text{mL}}\amp\amp\text{Write the rate as a ratio.}\\ \amp\approx\frac{19.3\,\text{g}}{1\,\text{mL}}\cdot\frac{16.39\,\text{mL}}{1\,\text{in}^3}\cdot\frac{1\,\text{oz}}{28.35\,\text{g}}\amp\amp\text{Use unit ratios to make cancellations.}\\ \amp=\frac{19.3\,\firstcancel{\text{g}}}{1\,\secondcancel{\text{mL}}}\cdot\frac{16.39\,\secondcancel{\text{mL}}}{1\,\text{in}^3}\cdot\frac{1\,\text{oz}}{28.35\,\firstcancel{\text{g}}}\amp\amp\text{Units may now cancel.}\\ \amp=\frac{19.3}{1}\cdot\frac{16.39}{1\,\text{in}^3}\cdot\frac{1\,\text{oz}}{28.35}\amp\amp\text{Only oz per cubic inch remain.}\\ \amp=\frac{19.3\cdot16.39}{28.35}\,\frac{\text{oz}}{\text{in}^3}\amp\amp\text{Multiply what's left and then divide.}\\ \amp\approx11.16\,\frac{\text{oz}}{\text{in}^3} \end{align*}

Notice that we did not need to raise any unit ratios to a power since there is a conversion fact that tells us that \(1\,\text{in}^3\approx16.39\,\text{mL}\text{.}\)

Thus, the density of gold is about 11.16 oz⁄in3.

Subsection 1.8.4 Absolute Value and Square Root

Example 1.8.14. Absolute Value.

The absolute value of a number is the distance from that number to \(0\) on the number line. An absolute value is always positive or \(0\text{.}\)

  1. \(\displaystyle \abs{2}=2\)

  2. \(\displaystyle \abs{-\frac{1}{2}}=\frac{1}{2}\)

  3. \(\displaystyle \abs{0}=0\)

Example 1.8.15. Square Root.

The symbol \(\sqrt{b}\) has meaning when \(b\geq0\text{.}\) It means the positive number that can be squared to result in \(b\text{.}\)

  1. \(\displaystyle \sqrt{9}=3\)

  2. \(\displaystyle \sqrt{2}\approx1.414\)

  3. \(\displaystyle \sqrt{\frac{9}{16}}=\frac{3}{4}\)

  4. \(\displaystyle \sqrt{-1}\text{ is undefined}\)

Subsection 1.8.5 Order of Operations

Example 1.8.16. Order of Operations.

When evaluating an expression with multiple operations, we must follow the order of operations:

  1. (P)arentheses and other grouping symbols

  2. (E)xponentiation

  3. (M)ultiplication, (D)ivision, and Negation

  4. (A)ddition and (S)ubtraction

\begin{align*} 4-2\left( 3-(2-4)^2 \right)\amp=4-2\left( 3-(\nextoperation{2-4})^2 \right)\\ \amp=4-2\left( 3-\nextoperation{(\highlight{-2})^2} \right)\\ \amp=4-2\left( \nextoperation{3-\highlight{4}} \right)\\ \amp=4-\nextoperation{2\left( \highlight{-1} \right)}\\ \amp=4-\highlight{(-2)}\\ \amp=6 \end{align*}

Subsection 1.8.6 Set Notation and Types of Numbers

A set is an unordered collection of items. Braces, \(\{{}\}\text{,}\) are used to show what items are in a set. For example, the set \(\{1,2,\pi\}\) is a set with three items that contains the numbers \(1\text{,}\) \(2\text{,}\) and \(\pi\text{.}\)

Types of Numbers.

Real numbers are categorized into the following sets: natural numbers, whole numbers, integers, rational numbers, and irrational numbers.

Example 1.8.17.

Here are some examples of numbers from each set of numbers:

Natural Numbers

The natural numbers are all counting numbers larger \(1\) and larger.

\(1,251,3462\)

Whole Numbers

The whole numbers are all counting numbers larger \(0\) and larger.

\(0,1,42,953\)

Integers

The integers are all counting numbers both negative and positive.

\(-263,-10,0,1,834\)

Rational Numbers

The rational numbers are all possible fractions of integers.

\(\frac{1}{3},-3,1.1,0,0.\overline{73}\)

Irrational Numbers

The irrational numbers are all numbers that cannot be written as a fraction of integers.

\(\pi,e,\sqrt{2}\)

Subsection 1.8.7 Comparison Symbols and Notation for Intervals

The following are symbols used to compare numbers.

Table 1.8.18. Comparison Symbols
Symbol Meaning Examples
\(=\) equals \(13=13\qquad\) \(\frac{5}{4}=1.25\)
\(\gt\) is greater than \(13\gt11\) \(\pi\gt3\)
\(\geq\) is greater than or equal to \(13\geq11\) \(3\geq3\)
\(\lt\) is less than \(-3\lt8\) \(\frac{1}{2}\lt\frac{2}{3}\)
\(\leq\) is less than or equal to \(-3\leq8\) \(3\leq3\)
\(\neq\) is not equal to \(10\neq20\) \(\frac{1}{2}\neq1.2\)

The following are some examples of set-builder notation and interval notation.

Graph

Set-Builder Notation

Interval Notation

a number line graph with a bracket at 1 opening to the right; a thick arrow points to the right

\(\left\{x\mid x\ge1\right\}\)

\([1,\infty)\)

a number line with a parenthesis opening to the right; a thick arrow points to the right

\(\left\{x\mid x\gt1\right\}\)

\((1,\infty)\)

a number line with a bracket at 1 opening to the left; a thick arrow points to the left

\(\left\{x\mid x\le1\right\}\)

\((-\infty,1]\)

a number line with a parenthesis at 1 opening to the left; a thick arrow points to the left

\(\left\{x\mid x\lt1\right\}\)

\((-\infty,1)\)

Exercises 1.8.8 Exercises

1.

Perform the given addition and subtraction.

  1. \({-15-7+\left(-9\right)}\)

  2. \({4-\left(-19\right)+\left(-10\right)}\)

2.

Perform the given addition and subtraction.

  1. \({-14-4+\left(-5\right)}\)

  2. \({1-\left(-19\right)+\left(-16\right)}\)

3.

Multiply the following.

  1. \((-1)\cdot(-4)\cdot(-2)\)

  2. \(6\cdot(-9)\cdot(-1)\)

  3. \((-85)\cdot(-76)\cdot0\)

4.

Multiply the following.

  1. \((-1)\cdot(-5)\cdot(-4)\)

  2. \(5\cdot(-9)\cdot(-3)\)

  3. \((-84)\cdot(-63)\cdot0\)

5.

Evaluate the following.

  1. \(\frac{-8}{-2}\)

  2. \(\frac{16}{-4}\)

  3. \(\frac{-50}{5}\)

6.

Evaluate the following.

  1. \(\frac{-100}{-10}\)

  2. \(\frac{70}{-7}\)

  3. \(\frac{-25}{5}\)

7.

Evaluate the following.

  1. \((-9)^{2}\)

  2. \(-6^{2}\)

8.

Evaluate the following.

  1. \((-7)^{2}\)

  2. \(-8^{2}\)

9.

Evaluate the following.

  1. \((-3)^{3}\)

  2. \(-4^{3}\)

10.

Evaluate the following.

  1. \((-3)^{3}\)

  2. \(-4^{3}\)

11.

Add: \(\displaystyle{-\frac{5}{6} + \frac{9}{10}}\)

12.

Add: \(\displaystyle{-\frac{5}{6} + \frac{7}{10}}\)

13.

Subtract: \(\displaystyle{-\frac{1}{10} - \left(-\frac{3}{5}\right)}\)

14.

Subtract: \(\displaystyle{-\frac{1}{6} - \left(-\frac{9}{10}\right)}\)

15.

Subtract: \(\displaystyle{ -5 - \frac{29}{9}}\)

16.

Subtract: \(\displaystyle{ -4 - \frac{11}{6}}\)

17.

Multiply: \(\displaystyle{-\frac{20}{3} \cdot \frac{7}{25}}\)

18.

Multiply: \(\displaystyle{-\frac{8}{3} \cdot \frac{7}{24}}\)

19.

Multiply: \(\displaystyle{-30\cdot \frac{7}{36} }\)

20.

Multiply: \(\displaystyle{-2\cdot \frac{9}{14} }\)

21.

Divide: \(\displaystyle{ \frac{7}{20} \div \left(-\frac{4}{15}\right) }\)

22.

Divide: \(\displaystyle{ \frac{3}{20} \div \left(-\frac{2}{15}\right) }\)

23.

Divide: \(\displaystyle{4 \div \frac{2}{5} }\)

24.

Divide: \(\displaystyle{18 \div \frac{9}{2} }\)

25.

Convert \({27\ {\rm oz}}\) to pounds.

26.

Convert \({5.4\ {\rm ns}}\) to seconds.

27.

Convert \({9.2\ {\rm ms}}\) to seconds.

28.

Convert \({48\ {\rm ms}}\) to seconds.

29.

Convert \({8.26\ {\rm mm}}\) to centimeters.

30.

Convert \({30.3\ {\rm min}}\) to days.

31.

Convert \({671\ {\rm mi^{2}}}\) to hectares.

32.

Convert \({1.57\ {\rm mi^{2}}}\) to square feet.

33.

Convert \({5.7\ {\rm mm^{3}}}\) to cubic meters.

34.

Convert \({27\ {\rm hm^{2}}}\) to square meters.

35.

Convert \({9.7\ {\rm mi^{3}}}\) to cubic kilometers.

36.

Convert \({6.7\ {\rm dm^{2}}}\) to square meters.

37.

Convert \({24\ {\textstyle\frac{\rm\mathstrut dm}{\rm\mathstrut ms}}}\) to meters per second.

38.

Convert \({6.02\ {\textstyle\frac{\rm\mathstrut ha}{\rm\mathstrut ms}}}\) to acres per second.

39.

Convert \({80.7\ {\textstyle\frac{\rm\mathstrut mL}{\rm\mathstrut d}}}\) to liters per week.

40.

Convert \({456\ {\textstyle\frac{\rm\mathstrut mg}{\rm\mathstrut wk}}}\) to grams per day.

41.

Convert \({8.23\ {\textstyle\frac{\rm\mathstrut Mb}{\rm\mathstrut wk}}}\) to kilobits per day.

42.

Convert \({31\ {\textstyle\frac{\rm\mathstrut mg}{\rm\mathstrut pt}}}\) to grams per quart.

Applications
43.

Morah’s bedroom has \({102\ {\rm ft^{2}}}\) of floor. She would like to carpet the floor, but carpeting is sold by the square yard. How many square yards of carpeting will she need to get?

44.

Andrew’s bedroom has \({115\ {\rm ft^{2}}}\) of floor. He would like to carpet the floor, but carpeting is sold by the square yard. How many square yards of carpeting will he need to get?

45.

Katherine is traveling in Europe and renting a car. She is used to thinking of gasoline amounts in gallons, but in Europe it is sold in liters. After filling the gas tank, she notices it took \({34\ {\rm L}}\) of gas. How many gallons is that?

46.

Stephanie is traveling in Europe and renting a car. She is used to thinking of gasoline amounts in gallons, but in Europe it is sold in liters. After filling the gas tank, she notices it took \({37\ {\rm L}}\) of gas. How many gallons is that?

47.

Emiliano found a family recipe from the old country that uses \({270\ {\rm mL}}\) of soup stock. The recipe serves four, but Emiliano wants to scale it up to serve eleven. And none of Emiliano’s measuring devices use the metric system. How many cups of soup stock should he use?

48.

Evan was driving at a steady speed of \({53\ {\rm mph}}\) for \(10\) minutes. How far did he travel in that time?

49.

The algae in a pond is growing at a rate of \({0.42\ {\textstyle\frac{\rm\mathstrut kg}{\rm\mathstrut d}}}\text{.}\) How much algae is in the pond after \(23\) weeks?

50.

Phil is downloading content at an average rate of \({91\ {\rm Mbps}}\) (megabits per second). After \(132\) minutes, how much has he downloaded? It is appropriate to express an amount of data like this in bytes, kilobytes, megabytes, gigabytes, or terabytes.

51.

Evaluate the following.

  1. \(\displaystyle{ - \lvert 2-10 \rvert = }\)

  2. \(\displaystyle{ \lvert -2-10 \rvert = }\)

  3. \(\displaystyle{ -4 \lvert 10-2 \rvert = }\)

52.

Evaluate the following.

  1. \(\displaystyle{ - \lvert 5-7 \rvert = }\)

  2. \(\displaystyle{ \lvert -5-7 \rvert = }\)

  3. \(\displaystyle{ -4 \lvert 7-5 \rvert = }\)

53.

Evaluate the following.

  1. \(\displaystyle{ \sqrt{9} }\) =

  2. \(\displaystyle{ \sqrt{64} }\) =

  3. \(\displaystyle{ \sqrt{121} }\) =

54.

Evaluate the following.

  1. \(\displaystyle{ \sqrt{25} }\) =

  2. \(\displaystyle{ \sqrt{9} }\) =

  3. \(\displaystyle{ \sqrt{16} }\) =

55.

Evaluate the following.

  1. \(\displaystyle{ \sqrt{{{\frac{36}{121}}}} }\) =

  2. \(\displaystyle{ \sqrt{{-{\frac{64}{81}}}} }\) =

56.

Evaluate the following.

  1. \(\displaystyle{ \sqrt{{{\frac{49}{64}}}} }\) =

  2. \(\displaystyle{ \sqrt{{-{\frac{1}{9}}}} }\) =

57.

Evaluate the following.

\(\displaystyle{ -8^{2}-3[ 5-( 6-3^{3} ) ] = }\)

58.

Evaluate the following.

\(\displaystyle{ -8^{2}-9[ 9-( 4-3^{3} ) ] = }\)

59.

Evaluate the following.

\(\displaystyle{ \frac{27-(-4)^{3}}{4-11} = }\)

60.

Evaluate the following.

\(\displaystyle{ \frac{27-(-2)^{3}}{8-13} = }\)

61.

Evaluate the following.

\(\displaystyle{ 2-8\left\lvert -9+(4-6)^{3}\right\rvert = }\)

62.

Evaluate the following.

\(\displaystyle{ 3-4\left\lvert -5+(3-6)^{3}\right\rvert = }\)

63.

Compare the following integers:

  1. \(-6\)

    • <

    • >

    • =

    \(8\)

  2. \(-6\)

    • <

    • >

    • =

    \(-8\)

  3. \(-6\)

    • <

    • >

    • =

    \(0\)

64.

Compare the following integers:

  1. \(4\)

    • <

    • >

    • =

    \(-5\)

  2. \(-2\)

    • <

    • >

    • =

    \(-5\)

  3. \(-5\)

    • <

    • >

    • =

    \(0\)

65.

Determine the validity of each statement by selecting True or False.

  1. The number \(\frac{\pi}{2}\) is rational

  2. The number \(\sqrt{\frac{9}{64}}\) is an integer, but not a whole number

  3. The number \(\sqrt{23}\) is rational

  4. The number \(\frac{-\sqrt{11}}{37\sqrt{11}}\) is irrational

  5. The number \(0\) is an integer

66.

Determine the validity of each statement by selecting True or False.

  1. The number \(\frac{5}{31}\) is rational, but not an integer

  2. The number \(-7\) is an integer that is also a natural number

  3. The number \(\frac{0}{1}\) is rational, but not a whole number

  4. The number \(\sqrt{17}\) is a real number, but not a rational number

  5. The number \(\sqrt{\frac{16}{64}}\) is rational, but not an integer

67.

A set is written using set-builder notation. Write it using interval notation.

\(\displaystyle{ \{ x \mid {{x}} \gt 6 \} }\)

68.

A set is written using set-builder notation. Write it using interval notation.

\(\displaystyle{ \{ x \mid {{x}} \gt 8 \} }\)

69.

For the interval expressed in the number line, write it using set-builder notation and interval notation.

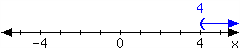
In set-builder notation:

In interval notation:

70.

For the interval expressed in the number line, write it using set-builder notation and interval notation.

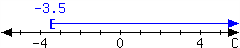
In set-builder notation:

In interval notation:

71.

For the interval expressed in the number line, write it using set-builder notation and interval notation.

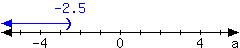
In set-builder notation:

In interval notation: