Section 10.4 Technical Definition of a Function
In Section 10.1, we discussed a conceptual understanding of functions and Definition 10.1.2. In this section we'll start with a more technical definition of what is a function, consistent with the ideas from Section 10.1.
Subsection 10.4.1 Formally Defining a Function
Definition 10.4.1. Function (Technical Definition).
A function is a collection of ordered pairs \((x,y)\) such that any particular value of \(x\) is paired with at most one value for \(y\text{.}\)
How is this definition consistent with the informal Definition 10.1.2, which describes a function as a process? Well, if you have a collection of ordered pairs \((x,y)\text{,}\) you can choose to view the left number as an input and the right value as the output. If the function's name is \(f\) and you want to find \(f(x)\) for a particular number \(x\text{,}\) look in the collection of ordered pairs to see if \(x\) appears among the first coordinates. If it does, then \(f(x)\) is the (unique) \(y\)-value it was paired with. If it does not, then that \(x\) is just not in the domain of \(f\text{,}\) because you have no way to determine what \(f(x)\) would be.
Example 10.4.2.
Using Definition 10.4.1, a function \(f\) could be given by
What is \(f(1)?\) Since the ordered pair \((1,4)\) appears in the collection of ordered pairs, we would say that \(f(1)=4\text{.}\)
What is \(f(2)?\) Since the ordered pair \((2,3)\) appears in the collection of ordered pairs, we would say that \(f(2)=3\text{.}\)
What is \(f(3)?\) None of the ordered pairs in the collection start with \(3\text{,}\) so \(f(3)\) is undefined, and we would say that \(3\) is not in the domain of \(f\text{.}\)
Let's spend some time seeing how this new definition applies to things that we already understand as functions from Section 10.1.
Example 10.4.3. A Function Given as a Table.
Consider the function \(g\) expressed by Table 10.4.4. How is this “a collection of ordered pairs?” With tables the connection is most easily apparent. Pair off each \(x\)-value with its \(y\)-value.
| \(x\) | \(g(x)\) |
| 12 | \(0.16\) |
| 15 | \(3.2\) |
| 18 | \(1.4\) |
| 21 | \(1.4\) |
| 24 | \(0.98\) |
In this case, we can view this function as:
Example 10.4.5. A Function Given as a Formula.
Consider the function \(h\) expressed by the formula \(h(x)=x^2\text{.}\) How is this “a collection of ordered pairs?”
This time, the collection is really big. Imagine an \(x\)-value, like \(x=2\text{.}\) We can calculate that \(f(2)=2^2=4\text{.}\) So the input \(2\) pairs with the output \(4\) and the ordered pair \((2,4)\) is part of the collection.
You could move on to any \(x\)-value, like say \(x=2.1\text{.}\) We can calculate that \(f(2.1)=2.1^2=4.41\text{.}\) So the input \(2.1\) pairs with the output \(4.41\) and the ordered pair \((2.1,4.41)\) is part of the collection.
The collection is so large that we cannot literally list all the ordered pairs as was done in Example 10.4.2 and Example 10.4.3. We just have to imagine this giant collection of ordered pairs. And if it helps to conceptualize it, we know that the ordered pairs \((2,4)\) and \((2.1,4.41)\) are included.
Example 10.4.6. A Function Given as a Graph.
Consider the functions \(p\) and \(q\) expressed in Figure 10.4.7 and Figure 10.4.8. How is each of these “a collection of ordered pairs?”
In Figure 10.4.7, we see that \(p(1)=4\text{,}\) \(p(2)=3\text{,}\) \(p(5)=3\text{,}\) and \(p(6)=1\text{.}\) The graph literally is the collection
In Figure 10.4.8, we can see a few whole number function values, like \(q(0)=0\) and \(q(1)=2\text{.}\) But the entire curve has infinitely many points on it and we'd never be able to list them all. We just have to imagine the giant collection of ordered pairs. And if it helps to conceptualize it, we know that the ordered pairs \((0,0)\) and \((1,2)\) are included.
Subsection 10.4.2 Identifying What is Not a Function
Just because you have a set of order pairs, a table, a graph, or an equation, it does not necessarily mean that you have a function. Conceptually, whatever you have needs to give consistent outputs if you feed it the same input. More technically, the set of ordered pairs is not allowed to have two ordered pairs that have the same \(x\)-value, but different \(y\)-values.
Example 10.4.9.
Consider each set of ordered pairs. Does it make a function?
\(\displaystyle \left\{\left(5,9\right),\left(3,2\right),\left(\frac{1}{2},0.6\right),\left(5,1\right)\right\}\)
\(\displaystyle \left\{\left(-5,12\right),\left(3,7\right),\left(\sqrt{2},1\right),\left(-0.9,4\right)\right\}\)
\(\displaystyle \left\{\left(5,9\right),\left(3,9\right),\left(4.2,\sqrt{2}\right),\left(\frac{4}{3},\frac{1}{2}\right)\right\}\)
\(\displaystyle \left\{\left(5,9\right),\left(0.7,2\right),\left(\sqrt{25},3\right),\left(\frac{2}{3},\frac{3}{2}\right)\right\}\)
This set of ordered pairs is not a function. The problem is that it has both \((5,9)\) and \((5,1)\text{.}\) It uses the same \(x\)-value paired with two different \(y\)-values. We have no clear way to turn the input \(5\) into an output.
This set of ordered pairs is a function. It is a collection of ordered pairs and the \(x\)-values are never reused.
This set of ordered pairs is a function. It is a collection of ordered pairs and the \(x\)-values are never reused. You might note that the output value \(9\) appears twice, but that doesn't matter. That just tells us that the function turns \(5\) into \(9\) and it also turns \(3\) into \(9\text{.}\)
This set of ordered pairs is not a function, but it's a little tricky. One of the ordered pairs uses \(\sqrt{25}\) as an input value. But that is the same as \(5\text{,}\) which is also used as an input value in another ordered pair.
Now that we understand how some sets of ordered pairs might not be functions, what about tables, graphs, and equations? If we are handed one of these things, can we tell whether or not it is giving us a function?
Checkpoint 10.4.10. Does This Table Make a Function?
Example 10.4.11. Does This Graph Make a Function?
Which of these graphs make \(y\) a function of \(x\text{?}\)
The graph in Figure 10.4.12 does not make \(y\) a function of \(x\text{.}\) Two ordered pairs on that graph are \((-3,1)\) and \((-3,-2)\text{,}\) so an input value is used twice with different output values.
The graph in Figure 10.4.13 does not make \(y\) a function of \(x\text{.}\) There are many ordered pairs with the same input value, but different output values. For example, \((2,-2)\) and \((2,4)\text{.}\)
The graph in Figure 10.4.14 does make \(y\) a function of \(x\text{.}\) It appears that no matter what \(x\)-value you choose on the \(x\)-axis, there is exactly one \(y\)-value paired up with it on the graph.
The graph in Figure 10.4.15 does make \(y\) a function of \(x\text{,}\) but we should discuss. The hollow dots on the line indicate that the line goes right up to that point, but never reaches it. We say there is a “hole” in the graph at these points. For two of these holes, there is a separate ordered pair immediately above or below the hole. The graph has the ordered pair \((-4,4)\text{.}\) It also has ordered pairs like \((\text{very close to }{-4},\text{very close to }0)\text{,}\) but it does not have \((-4,0)\text{.}\) Overall, there is no \(x\)-value that is used twice with different \(y\)-values, so this graph does make \(y\) a function of \(x\)
The graph in Figure 10.4.13 does not make \(y\) a function of \(x\text{.}\) There are many ordered pairs with the same input value, but different output values. For example, \((0,1)\text{,}\) \((0,3)\text{,}\) \((0,-1)\text{,}\) \((0,5)\text{,}\) and \((0,-6)\) all use \(x=0\text{.}\)
The graph in Figure 10.4.13 does not make \(y\) a function of \(x\text{.}\) There are many ordered pairs with the same input value, but different output values. For example at \(x=2\text{,}\) there is both a positive and a negative associated \(y\)-value. It's hard to say exactly what these \(y\)-values are, but we don't have to.
This last set of examples might reveal something to you. For instance in Figure 10.4.13, the issue is that there are places on the graph with the same \(x\)-value, but different \(y\)-values. Visually, what that means is there are places on the graph that are directly above/below each other. Thinking about this leads to a quick visual “test” to determine if a graph gives \(y\) as a function of \(x\text{.}\)
Fact 10.4.18. Vertical Line Test.
Given a graph in the \(xy\)-plane, if a vertical line ever touches it in more than one place, the graph does not give \(y\) as a function of \(x\text{.}\) If vertical lines only ever touch the graph once or never at all, then the graph does give \(y\) as a function of \(x\text{.}\)
Example 10.4.19.
In each graph from Example 10.4.11, we can apply the Vertical Line Test.
Lastly, we come to equations. Certain equations with variables \(x\) and \(y\) clearly make \(y\) a function of \(x\text{.}\) For example, \(y=x^2+1\) says that if you have an \(x\)-value, all you have to do is substitute it into that equation and you will have determined an output \(y\)-value. You could then name the function \(f\) and give a formula for it: \(f(x)=x^2+1\text{.}\)
With other equations, it may not be immediately clear whether or not they make \(y\) a function of \(x\text{.}\)
Example 10.4.26.
Do each of these equations make \(y\) a function of \(x\text{?}\)
\(\displaystyle 2x+3y=5\)
\(\displaystyle y=\pm\sqrt{x+4}\)
\(\displaystyle x^2+y^2=9\)
-
The equation \(2x+3y=5\) does make \(y\) a function of \(x\text{.}\) Here are three possible explanations.
You recognize that the graph of this equation would be a non-vertical line and so it would pass the Vertical Line Test.
Imagine that you have a specific value for \(x\) and you substitute it in to \(2x+3y=5\text{.}\) Will you be able to use algebra to solve for \(y\text{?}\) All you will need is to simplify, subtract from both sides, and divide on both sides, so you will be able to determine \(y\text{.}\)
Can you just isolate \(y\) in terms of \(x\text{?}\) Yes, a few steps of algebra can turn \(2x+3y=5\) into \(y=\frac{5-2x}{3}\text{.}\) Now you have an explicit formula for \(y\) in terms of \(x\text{,}\) so \(y\) is a function of \(x\text{.}\)
The equation \(y=\pm\sqrt{x+4}\) does not make \(y\) a function of \(x\text{.}\) Just having the \(\pm\) (plus or minus) in the equation immediately tells you that for almost any valid \(x\)-value, there would be two associated \(y\)-values.
-
The equation \(x^2+y^2=9\) does not make \(y\) a function of \(x\text{.}\) Here are three possible explanations.
Imagine that you have a specific value for \(x\) and you substitute it in to \(x^2+y^2=9\text{.}\) Will you be able to use algebra to solve for \(y\text{?}\) For example, if you substitute in \(x=1\text{,}\) then you have \(1+y^2=9\text{,}\) which simplifies to \(y^2=8\text{.}\) Can you really determine what \(y\) is? No, because it could be \(\sqrt{8}\) or it could be \(-\sqrt{8}\text{.}\) So this equation does not provide you with a way to turn \(x\)-values into \(y\)-values.
Can you just isolate \(y\) in terms of \(x\text{?}\) You might get started and use algebra to convert \(x^2+y^2=9\) into \(y^2=9-x^2\text{.}\) But what now? The best you can do is acknowledge that \(y\) is either the positive or the negative square root of \(9 - x^2\text{.}\) You might write \(y=\pm\sqrt{9-x^2}\text{.}\) But now for almost any valid \(x\)-value, there are two associated \(y\)-values.
You recognize that the graph of this equation would be a circle with radius \(3\) and so it would not pass the Vertical Line Test.
Checkpoint 10.4.27.
Exercises 10.4.3 Exercises
Determining If Sets of Ordered Pairs Are Functions
1.
Do these sets of ordered pairs make functions of \(x\text{?}\) What are their domains and ranges?
-
\(\Big\{(2,8),(6,9)\Big\}\)
This set of ordered pairs
describes
does not describe
-
\(\Big\{(-9,8),(9,2),(8,3)\Big\}\)
This set of ordered pairs
describes
does not describe
-
\(\Big\{(2,7),(4,9),(4,2),(1,2)\Big\}\)
This set of ordered pairs
describes
does not describe
-
\(\Big\{(1,7),(1,3),(-7,1),(5,1),(-1,6)\Big\}\)
This set of ordered pairs
describes
does not describe
2.
Do these sets of ordered pairs make functions of \(x\text{?}\) What are their domains and ranges?
-
\(\Big\{(-3,5),(-4,2)\Big\}\)
This set of ordered pairs
describes
does not describe
-
\(\Big\{(-5,6),(-1,5),(-6,1)\Big\}\)
This set of ordered pairs
describes
does not describe
-
\(\Big\{(4,8),(2,9),(4,10),(-2,5)\Big\}\)
This set of ordered pairs
describes
does not describe
-
\(\Big\{(5,7),(9,10),(-4,3),(1,3),(-9,10)\Big\}\)
This set of ordered pairs
describes
does not describe
3.
Does the following set of ordered pairs make for a function of \(x\text{?}\)
\(\Big\{(-9,8),(0,6),(-3,9),(-1,3),(-5,8)\Big\}\)
This set of ordered pairs
describes
does not describe
4.
Does the following set of ordered pairs make for a function of \(x\text{?}\)
\(\Big\{(10,9),(-4,1),(-4,8),(1,9),(5,3)\Big\}\)
This set of ordered pairs
describes
does not describe
Domain and Range
5.
Below is all of the information that exists about a function \(f\text{.}\)
\(\begin{aligned} f(0)\amp =4\amp f(2)\amp =-3\amp f(4)\amp =3 \end{aligned}\)
Write \(f\) as a set of ordered pairs.
\(f\) has domain and range .
6.
Below is all of the information that exists about a function \(f\text{.}\)
\(\begin{aligned} f(3)\amp =3\amp f(5)\amp =-3\amp f(8)\amp =-3 \end{aligned}\)
Write \(f\) as a set of ordered pairs.
\(f\) has domain and range .
7.
Below is all of the information that exists about a function \(g\text{.}\)
\(\begin{aligned} g(1)\amp =1\amp g(3)\amp =10\amp g(4)\amp =3 \end{aligned}\)
Write \(g\) as a set of ordered pairs.
\(g\) has domain and range .
8.
Below is all of the information about a function \(h\text{.}\)
\(\begin{aligned} h(a)\amp =2\amp h(b)\amp =6\\ h(c)\amp =4\amp h(d)\amp =4 \end{aligned}\)
Write \(h\) as a set of ordered pairs.
\(h\) has domain and range .
9.
Below is all of the information about a function \(F\text{.}\)
\(\begin{aligned} F(a)\amp =5\amp F(b)\amp =-2\\ F(c)\amp =1\amp F(d)\amp =1 \end{aligned}\)
Write \(F\) as a set of ordered pairs.
\(F\) has domain and range .
10.
Below is all of the information about a function \(G\text{.}\)
\(\begin{aligned} G(a)\amp =4\amp G(b)\amp =4\\ G(c)\amp =-2\amp G(d)\amp =-2 \end{aligned}\)
Write \(G\) as a set of ordered pairs.
\(G\) has domain and range .
Determining If Graphs Are Functions
11.
Decide whether each graph shows a relationship where \(y\) is a function of \(x\text{.}\)
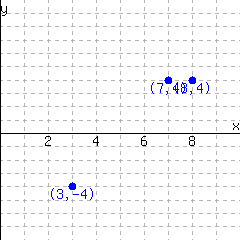
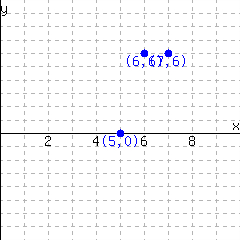
The first graph
does
does not
does
does not
12.
Decide whether each graph shows a relationship where \(y\) is a function of \(x\text{.}\)
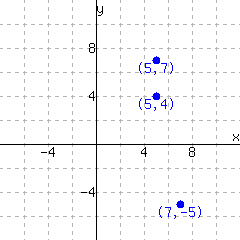
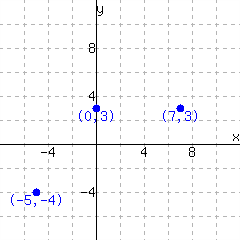
The first graph
does
does not
does
does not
13.
The following graphs show two relationships. Decide whether each graph shows a relationship where \(y\) is a function of \(x\text{.}\)
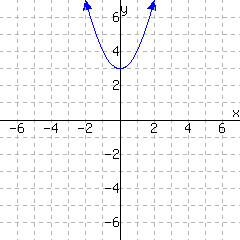
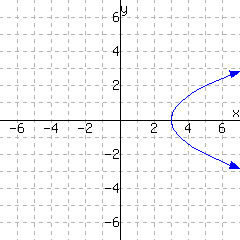
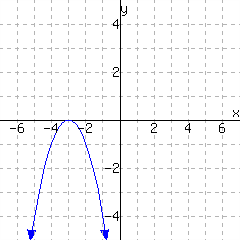
The first graph
does
does not
does
does not
14.
The following graphs show two relationships. Decide whether each graph shows a relationship where \(y\) is a function of \(x\text{.}\)
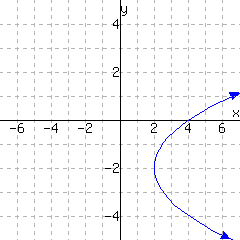
The first graph
does
does not
does
does not
Determining If Equations Are Functions
15.
Select all of the following relations that make \(y\) a function of \(x\text{.}\) There are several correct answers.
\(\displaystyle y=x^{5}\)
\(\displaystyle y=\frac{x+2}{6-x}\)
\(\displaystyle \left| y\right|=x\)
\(\displaystyle x=y^{9}\)
\(\displaystyle x^2+y^2=64\)
\(\displaystyle y=\frac{1}{x^{4}}\)
\(\displaystyle y=\left| x \right|\)
\(\displaystyle 2 x+ 5 y=1\)
\(\displaystyle x=y^{8}\)
\(\displaystyle y=\sqrt[5]{x}\)
\(\displaystyle y=\sqrt{100-x^2}\)
\(\displaystyle y=\pm\sqrt{100-x^2}\)
16.
Select all of the following relations that make \(y\) a function of \(x\text{.}\) There are several correct answers.
\(\displaystyle y=\sqrt{49-x^2}\)
\(\displaystyle 3 x+ 3 y=1\)
\(\displaystyle x=y^{8}\)
\(\displaystyle y=\frac{1}{x^{2}}\)
\(\displaystyle y=\pm\sqrt{49-x^2}\)
\(\displaystyle y=\frac{x+4}{2-x}\)
\(\displaystyle \left| y\right|=x\)
\(\displaystyle y=\sqrt[3]{x}\)
\(\displaystyle y=x^{4}\)
\(\displaystyle x^2+y^2=9\)
\(\displaystyle y=\left| x \right|\)
\(\displaystyle x=y^{9}\)
Determining If Tables Are Functions
17.
Determine whether or not each of the following tables could be the table of values of a function. If the table can not be the table of values of a function, give an input that has more than one possible output.
| Input | Output |
| \(2\) | \(-6\) |
| \(4\) | \(-13\) |
| \(6\) | \(-6\) |
| \(8\) | \(-4\) |
| \(-2\) | \(15\) |
Could this be the table of values for a function?
yes
no
If not, which input has more than one possible output?
-2
2
4
6
8
None, the table could be the table of values of a function.
| Input | Output |
| \(-4\) | \(9\) |
| \(-3\) | \(-3\) |
| \(-2\) | \(8\) |
| \(-3\) | \(25\) |
| \(-1\) | \(2\) |
Could this be the table of values for a function?
yes
no
If not, which input has more than one possible output?
-4
-3
-2
-1
None, the table could be the table of values of a function.
18.
Determine whether or not each of the following tables could be the table of values of a function. If the table can not be the table of values of a function, give an input that has more than one possible output.
| Input | Output |
| \(2\) | \(-1\) |
| \(4\) | \(13\) |
| \(6\) | \(-1\) |
| \(8\) | \(-15\) |
| \(-2\) | \(14\) |
Could this be the table of values for a function?
yes
no
If not, which input has more than one possible output?
-2
2
4
6
8
None, the table could be the table of values of a function.
| Input | Output |
| \(-4\) | \(-12\) |
| \(-3\) | \(-1\) |
| \(-2\) | \(-16\) |
| \(-3\) | \(11\) |
| \(-1\) | \(20\) |
Could this be the table of values for a function?
yes
no
If not, which input has more than one possible output?
-4
-3
-2
-1
None, the table could be the table of values of a function.
