Skip to main content

Section 4.10 Graphing Lines Chapter Review

Subsection 4.10.1 Cartesian Coordinates

In SectionĀ 4.1 we covered the definition of the Cartesian Coordinate System and how to plot points using the \(x\) and \(y\)-axes.

Example 4.10.1.

On paper, sketch a Cartesian coordinate system with units, and then plot the following points: \((3,2),(-5,-1),(0,-3),(4,0)\text{.}\)

Explanation
a Cartesian grid with four points plotted; the point (3,2) is 3 units to the right of the origin and two units up; the point (-5,-1) is 5 units to the left of the origin and 1 unit down; the point (0,-3) is on the y-axis 3 units down; the point (4,0) is right 4 units along the x-axis.
Figure 4.10.2. A Cartesian grid with the four points plotted.

Subsection 4.10.2 Graphing Equations

In SectionĀ 4.2 we covered how to find and plot solutions to equations, by choosing some reasonable \(x\)-values, calculating the corresponding \(y\)-values, plotting the \((x,y)\)-pairs as points and connecting the points with a smooth curve, to produce a graph of the equation.

Example 4.10.3.

Graph the equation \(y=-2x+5\text{.}\)

Explanation
\(x\) \(y=-2x+5\) Point
\(-2\) \(\phantom{-2(-2)+5=\substitute{9}}\) \(\phantom{(-2,9)}\)
\(-1\) \(\phantom{-2(-1)+5=\substitute{7}}\) \(\phantom{(-1,7)}\)
\(0\) \(\phantom{-2(0)+5=\substitute{5}}\) \(\phantom{(0,5)}\)
\(1\) \(\phantom{-2(1)+5=\substitute{3}}\) \(\phantom{(1,3)}\)
\(2\) \(\phantom{-2(2)+5=\substitute{1}}\) \(\phantom{(2,1)}\)
(a) Set up the table
\(x\) \(y=-2x+5\) Point
\(-2\) \(-2(-2)+5=\substitute{9}\) \((-2,9)\)
\(-1\) \(-2(-1)+5=\substitute{7}\) \((-1,7)\)
\(0\) \(-2(0)+5=\substitute{5}\) \((0,5)\)
\(1\) \(-2(1)+5=\substitute{3}\) \((1,3)\)
\(2\) \(-2(2)+5=\substitute{1}\) \((2,1)\)
(b) Complete the table
Figure 4.10.4. Making a table for \(y=-2x+5\)

We use points from the table to graph the equation. First, plot each point carefully. Then, connect the points with a smooth curve. Here, the curve is a straight line. Lastly, we can communicate that the graph extends further by sketching arrows on both ends of the line.

a Cartesian grid with points (-2,9),(-1,7),(0,5),(1,3),(2,1)
(a) Use points from the table
a Cartesian grid with points (-2,9),(-1,7),(0,5),(1,3),(2,1);they are connected with a solid line with arrows on each end
(b) Connect the points in whatever pattern is apparent
Figure 4.10.5. Graphing the Equation \(y=-2x+5\)

Subsection 4.10.3 Exploring Two-Variable Data and Rate of Change

In SectionĀ 4.3 we covered how to find patterns in tables of data and how to calculate the rate of change between points in data.

Exploring Two-Variable Data and Rate of Change.

For a linear relationship, by its data in a table, we can see the rate of change (slope) and the line's \(y\)-intercept, thus writing the equation.

Example 4.10.6.

Write an equation in the form \(y=\ldots\) suggested by the pattern in the table.

Table 4.10.7. A table of linear data.
\(x\) \(y\)
\(0\) \(-4\)
\(1\) \(-6\)
\(2\) \(-8\)
\(3\) \(-10\)
Explanation

We consider how the values change from one row to the next. From row to row, the \(x\)-value increases by \(1\text{.}\) Also, the \(y\)-value decreases by \(2\) from row to row.

\(x\) \(y\)
\(0\) \(-4\)
\({}+1\rightarrow\) \(1\) \(-6\) \(\leftarrow{}-2\)
\({}+1\rightarrow\) \(2\) \(-8\) \(\leftarrow{}-2\)
\({}+1\rightarrow\) \(3\) \(-10\) \(\leftarrow{}-2\)

Since row-to-row change is always \(1\) for \(x\) and is always \(-2\) for \(y\text{,}\) the rate of change from one row to another row is always the same: \(-2\) units of \(y\) for every \(1\) unit of \(x\text{.}\)

We know that the output for \(x = 0\) is \(y = -4\text{.}\) And our observation about the constant rate of change tells us that if we increase the input by \(x\) units from \(0\text{,}\) the ouput should decrease by \(\overbrace{(-2)+(-2)+\cdots+(-2)}^{x\text{ times}}\text{,}\) which is \(-2x\text{.}\) So the output would be \(-4-2x\text{.}\)

So the equation is \(y=-2x-4\text{.}\)

Subsection 4.10.4 Slope

In SectionĀ 4.4 we covered the definition of slopeĀ 4.4.2 and how to use slope-triangles to calculate slope. There is also the slope formula which helps find the slope through any two points.

Example 4.10.8.

Find the slope of the line in the following graph.

This is a grid with a line, passing the points (3,15) and (6,27).
Figure 4.10.9. The line with two points indicated.
Explanation
This is a grid with a line, passing the points (3,15) and (6,27). A slope triangle is drawn, starting at (3,15), passing (6,15), and ends at (6,27). The label from (3,15) to (6,15) is "6-3=3"; the label from (6,15) to (6,27) is "27-15=12".
Figure 4.10.10. The line with a slope triangle drawn.

We picked two points on the line and then drew a slope triangle. Next, we will do:

\begin{equation*} \text{slope}=\frac{12}{3}=4 \end{equation*}

The line's slope is \(4\text{.}\)

Example 4.10.11. Finding a Line's Slope by the Slope Formula.

Use the slope formula to find the slope of the line that passes through the points \((-5,25)\) and \((4,-2)\text{.}\)

Explanation
\begin{align*} \text{slope}\amp=\frac{y_2-y_1}{x_2-x_1}\\ \amp=\frac{-2-(25)}{4-(-5)}\\ \amp=\frac{-27}{9}\\ \amp=-3 \end{align*}

The line's slope is \(-3\text{.}\)

Subsection 4.10.5 Slope-Intercept Form

In SectionĀ 4.5 we covered the definition of slope intercept-form and both wrote equations in slope-intercept form and graphed lines given in slope-intercept form.

Example 4.10.12.

Graph the line \(y=-\frac{5}{2}x+4\text{.}\)

Explanation
a Cartesian grid with the point (0,4) plotted
(a) First, plot the line's \(y\)-intercept, \((0,4)\text{.}\)
the previous plot of the y-intercept with slope triangles drawn; they go right 2 and down 5 twice to the right; from the y-intercept they also go up 5 and left 2 once; the points plotted are (-2,9), (0,4), (2,-1), (4,-6)
(b) The slope is \(-\frac{5}{2}=\frac{-5}{2}=\frac{5}{-2}\text{.}\) So we can try using a ā€œrunā€ of \(2\) and a ā€œriseā€ of \(-5\) or a ā€œrunā€ of \(-2\) and a ā€œriseā€ of \(5\text{.}\)
the previous plot with a solid line drawn through all of the points; there are arrowheads on each end of the line
(c) Arrowheads and labels are encouraged.
Figure 4.10.13. Graphing \(y=-\frac{5}{2}x+4\)
Writing a Line's Equation in Slope-Intercept Form Based on Graph.

Given a line's graph, we can identify its \(y\)-intercept and then find its slope by a slope triangle. With a line's slope and \(y\)-intercept, we can write its equation in the form of \(y=mx+b\text{.}\)

Example 4.10.14.

Find the equation of the line in the graph.

a coordinate graph of a line;three points on the line are (-3,12),(0,10) and (3,8)
Figure 4.10.15. Graph of a line
Explanation
the previous graph showing the line crosses the y-axis at 10 or (0,10)
Figure 4.10.16. Identify the line's \(y\)-intercept, \(10\text{.}\)
the previous graph with slope triangles drawn moving right 3 units and down two units
Figure 4.10.17. Identify the line's slope by a slope triangle. Note that we can pick any two points on the line to create a slope triangle. We would get the same slope: \(-\frac{2}{3}\)

With the line's slope \(-\frac{2}{3}\) and \(y\)-intercept \(10\text{,}\) we can write the line's equation in slope-intercept form: \(y=-\frac{2}{3}x+10\text{.}\)

Subsection 4.10.6 Point-Slope Form

In SectionĀ 4.6 we covered the definition of point-slope form and both wrote equations in point-slope form and graphed lines given in point-slope form.

Example 4.10.18.

A line passes through \((-6,0)\) and \((9,-10)\text{.}\) Find this line's equation in point-slope form.

Explanation

We will use the slope formula to find the slope first. After labeling those two points as \((\overset{x_1}{-6},\overset{y_1}{0}) \text{ and } (\overset{x_2}{9},\overset{y_2}{-10})\text{,}\) we have:

\begin{align*} \text{slope}\amp=\frac{y_2-y_1}{x_2-x_1}\\ \amp=\frac{-10-0}{9-(-6)}\\ \amp=\frac{-10}{15}\\ \amp=-\frac{2}{3} \end{align*}

Now the point-slope equation looks like \(y=-\frac{2}{3}(x-x_0)+y_0\text{.}\) Next, we will use \((9,-10)\) and substitute \(x_0\) with \(9\) and \(y_0\) with \(-10\text{,}\) and we have:

\begin{align*} y\amp=-\frac{2}{3}(x-x_0)+y_0\\ y\amp=-\frac{2}{3}(x-9)+(-10)\\ y\amp=-\frac{2}{3}(x-9)-10 \end{align*}

Subsection 4.10.7 Standard Form

In SectionĀ 4.7 we covered the definition of standard form of a linear equation. We converted equations from standard form to slope-intercept form and vice versa. We also graphed lines from standard form by finding the intercepts of the line.

Example 4.10.19.

  1. Convert \(2x+3y=6\) into slope-intercept form.

  2. Convert \(y=-\frac{4}{7}x-3\) into standard form.

Explanation
  1. \begin{align*} 2x+3y\amp=6\\ 2x+3y\subtractright{2x}\amp=6\subtractright{2x}\\ 3y\amp=-2x+6\\ \divideunder{3y}{3}\amp=\divideunder{-2x+6}{3}\\ y\amp=\frac{-2x}{3}+\frac{6}{3}\\ y\amp=-\frac{2}{3}x+2 \end{align*}

    The line's equation in slope-intercept form is \(y=-\frac{2}{3}x+2\text{.}\)

  2. \begin{align*} y\amp=-\frac{4}{7}x-3\\ \multiplyleft{7}y\amp=\multiplyleft{7}(-\frac{4}{7}x-3)\\ 7y\amp=7\cdot(-\frac{4}{7}x)-7\cdot3\\ 7y\amp=-4x-21\\ 7y\addright{4x}\amp=-4x-21\addright{4x}\\ 4x+7y\amp=-21 \end{align*}

    The line's equation in standard form is \(4x+7y=-21\text{.}\)

To graph a line in standard form, we could first change it to slope-intercept form, and then graph the line by its \(y\)-intercept and slope triangles. A second method is to graph the line by its \(x\)-intercept and \(y\)-intercept, which is preferable when the \(y\)-intercept doesn't have an integer as its \(y\)-coordinate.

Example 4.10.20.

Graph \(2x-3y=-6\) using its intercepts. Then use the intercepts to calculate the line's slope.

Explanation

We calculate the line's \(x\)-intercept by substituting \(y=0\) into the equation

\begin{align*} 2x-3y\amp=-6\\ 2x-3(\substitute{0})\amp=-6\\ 2x\amp=-6\\ x\amp=-3 \end{align*}

So the line's \(x\)-intercept is \((-3,0)\text{.}\)

Similarly, we substitute \(x=0\) into the equation to calculate the \(y\)-intercept:

\begin{align*} 2x-3y\amp=-6\\ 2(\substitute{0})-3y\amp=-6\\ -3y\amp=-6\\ y\amp=2 \end{align*}

So the line's \(y\)-intercept is \((0,2)\text{.}\)

Let's find a checkpoint for this line by choosing \(x=-1\text{.}\) Notice that this \(x\) value falls between the \(x\)-coordinates of the two intercepts we've already found. Next, we plug that value in for \(x\) and solve for \(y\text{:}\)

\begin{align*} 2x-3y\amp=-6\\ 2(\substitute{-1})-3y\amp=-6\\ -2-3y\amp=-6\\ -3y\amp=-4\\ y\amp=\frac{4}{3} \end{align*}

So the checkpoint is \(\left(-1,\frac{4}{3}\right)\text{.}\)

With both the intercepts' and the checkpoint's coordinates, we can graph the line:

a coordinate grid with the graph of line 2x-3y=-6; the x-intercept is (-3,0) and the y-intercept is (0,2)
Figure 4.10.21. Graph of \(2x-3y=-6\)

Now that we have graphed the line we can read the slope. The rise is 2 units and the run is 3 units so the slope is \(\frac{2}{3}\text{.}\)

Subsection 4.10.8 Horizontal, Vertical, Parallel, and Perpendicular Lines

In SectionĀ 4.8 we covered what equations of horizontal and vertical lines. We also covered the relationships between the slopes of parallel and perpendicular lines.

Example 4.10.22.

Line \(m\)'s equation is \(y=-2x+20\text{.}\) Line \(n\) is parallel to \(m\) and line \(n\) also passes through the point \((4,-3)\text{.}\) Find an equation for line \(n\) in point slope form.

Explanation

Since parallel lines have the same slope, line \(n\)'s slope is also \(-2\text{.}\) Since line \(n\) also passes the point \((4,-3)\text{,}\) we can write line \(n\)'s equation in point-slope form:

\begin{align*} y\amp=m(x-x_1)+y_1\\ y\amp=-2(x-4)+(-3)\\ y\amp=-2(x-4)-3 \end{align*}

Two lines are perpendicular if and only if the product of their slopes is \(-1\text{.}\)

Example 4.10.23.

Line \(m\)'s equation is \(y=-2x+20\text{.}\) Line \(n\) is perpendicular to \(m\) and line \(q\) also passes through the point \((4,-3)\text{.}\) Find an equation for line \(q\) in slope intercept form.

Explanation

Since line \(m\) and \(q\) are perpendicular, the product of their slopes is \(-1\text{.}\) Because line \(m\)'s slope is given as \(-2\text{,}\) we can find line \(q\)'s slope is \(\frac{1}{2}\text{.}\)

Since line \(q\) also passes the point \((4,-3)\text{,}\) we can write line \(q\)'s equation in point-slope form:

\begin{align*} y\amp=m(x-x_1)+y_1\\ y\amp=\frac{1}{2}(x-4)+(-3)\\ y\amp=\frac{1}{2}(x-4)-3 \end{align*}

We can now convert this equation to slope-intercept form:

\begin{align*} y\amp=\frac{1}{2}(x-4)-3\\ y\amp=\frac{1}{2}x-2-3\\ y\amp=\frac{1}{2}x-5 \end{align*}

Exercises 4.10.9 Exercises

1.

Sketch the points \((8,2)\text{,}\) \((5,5)\text{,}\) \((-3,0)\text{,}\) \(\left(0,-\frac{14}{3}\right)\text{,}\) \((3,-2.5)\text{,}\) and \((-5,7)\) on a Cartesian plane.

2.

Locate each point in the graph:

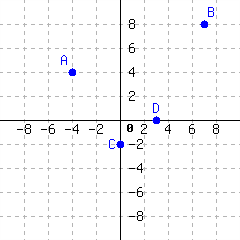
Write each pointā€™s position as an ordered pair, like \((1,2)\text{.}\)

\(A=\) \(B=\)
\(C=\) \(D=\)
3.

Consider the equation

\(y=-\frac{3}{4} x-2\)

Which of the following ordered pairs are solutions to the given equation? There may be more than one correct answer.

  • \(\displaystyle (0,-2)\)

  • \(\displaystyle (12,-7)\)

  • \(\displaystyle (-12,7)\)

  • \(\displaystyle (-4,5)\)

4.

Consider the equation

\(y=-\frac{5}{6} x-2\)

Which of the following ordered pairs are solutions to the given equation? There may be more than one correct answer.

  • \(\displaystyle (-24,23)\)

  • \(\displaystyle (-18,13)\)

  • \(\displaystyle (0,-2)\)

  • \(\displaystyle (24,-17)\)

5.

Write an equation in the form \(y=\ldots\) suggested by the pattern in the table.

\(x\) \(y\)
\(0\) \({-4}\)
\(1\) \({-2}\)
\(2\) \({0}\)
\(3\) \({2}\)
6.

Write an equation in the form \(y=\ldots\) suggested by the pattern in the table.

\(x\) \(y\)
\(0\) \({3}\)
\(1\) \({-2}\)
\(2\) \({-7}\)
\(3\) \({-12}\)
7.

Below is a lineā€™s graph.

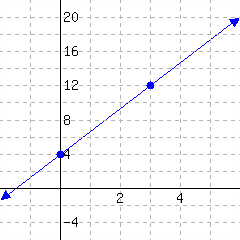
The slope of this line is .

8.

Below is a lineā€™s graph.

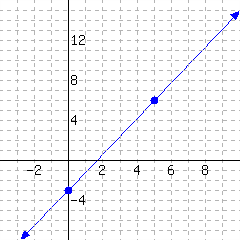
The slope of this line is .

9.

Below is a lineā€™s graph.

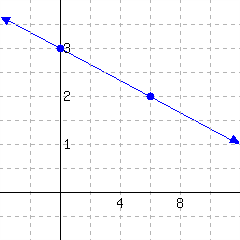
The slope of this line is .

10.

Below is a lineā€™s graph.

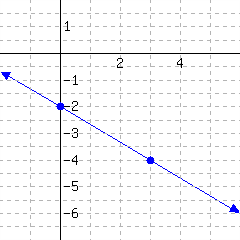
The slope of this line is .

11.

A line passes through the points \((-24,{18})\) and \((24,{-12})\text{.}\) Find this lineā€™s slope.

12.

A line passes through the points \((-12,{6})\) and \((8,{-19})\text{.}\) Find this lineā€™s slope.

13.

A line passes through the points \((1,1)\) and \((-3,1)\text{.}\) Find this lineā€™s slope.

14.

A line passes through the points \((5,3)\) and \((-1,3)\text{.}\) Find this lineā€™s slope.

15.

A line passes through the points \((5,-3)\) and \((5,2)\text{.}\) Find this lineā€™s slope.

16.

A line passes through the points \((8,-5)\) and \((8,4)\text{.}\) Find this lineā€™s slope.

17.

A lineā€™s graph is given. What is this lineā€™s slope-intercept equation?

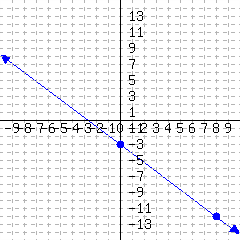
18.

A lineā€™s graph is given. What is this lineā€™s slope-intercept equation?

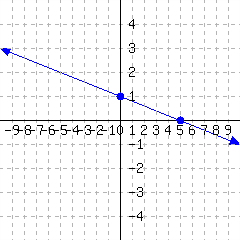
19.

Find the lineā€™s slope and \(y\)-intercept.

A line has equation \(\displaystyle{ 2x-3y=15 }\text{.}\)

This lineā€™s slope is .

This lineā€™s \(y\)-intercept is .

20.

Find the lineā€™s slope and \(y\)-intercept.

A line has equation \(\displaystyle{ 7x-4y=-4 }\text{.}\)

This lineā€™s slope is .

This lineā€™s \(y\)-intercept is .

21.

A line passes through the points \((-10,{-17})\) and \((-15,{-21})\text{.}\) Find this lineā€™s equation in point-slope form.

22.

A line passes through the points \((-4,{-15})\) and \((0,{-5})\text{.}\) Find this lineā€™s equation in point-slope form.

23.

Scientists are conducting an experiment with a gas in a sealed container. The mass of the gas is measured, and the scientists realize that the gas is leaking over time in a linear way. Each minute, they lose 7.1 grams. minutes since the experiment started, the remaining gas had a mass of 269.8 grams.

Let \(x\) be the number of minutes that have passed since the experiment started, and let \(y\) be the mass of the gas in grams at that moment. Use a linear equation to model the weight of the gas over time.

  1. Find this lineā€™s slope-intercept equation.

  2. 35 minutes after the experiment started, how many grams of gas would be left?

  3. If a linear model continues to be accurate, after how many minutes since the experiment started will all gas in the container will be gone?

24.

Scientists are conducting an experiment with a gas in a sealed container. The mass of the gas is measured, and the scientists realize that the gas is leaking over time in a linear way. Each minute, they lose 4 grams. minutes since the experiment started, the remaining gas had a mass of 172 grams.

Let \(x\) be the number of minutes that have passed since the experiment started, and let \(y\) be the mass of the gas in grams at that moment. Use a linear equation to model the weight of the gas over time.

  1. Find this lineā€™s slope-intercept equation.

  2. 35 minutes after the experiment started, how many grams of gas would be left?

  3. If a linear model continues to be accurate, after how many minutes since the experiment started will all gas in the container will be gone?

25.

Find the \(y\)-intercept and \(x\)-intercept of the line given by the equation. If a particular intercept does not exist, enter none into all the answer blanks for that row.

\begin{equation*} 8 x + 7 y = -112 \end{equation*}
\(x\)-value \(y\)-value Location (as an ordered pair)
\(y\)-intercept
\(x\)-intercept
26.

Find the \(y\)-intercept and \(x\)-intercept of the line given by the equation. If a particular intercept does not exist, enter none into all the answer blanks for that row.

\begin{equation*} 8 x + 5 y = -120 \end{equation*}
\(x\)-value \(y\)-value Location (as an ordered pair)
\(y\)-intercept
\(x\)-intercept
27.

Find the lineā€™s slope and \(y\)-intercept.

A line has equation \(\displaystyle{ -{2}x+y= -5 }\text{.}\)

This lineā€™s slope is .

This lineā€™s \(y\)-intercept is .

28.

Find the lineā€™s slope and \(y\)-intercept.

A line has equation \(\displaystyle{ -x-y= -7 }\text{.}\)

This lineā€™s slope is .

This lineā€™s \(y\)-intercept is .

29.

Find the lineā€™s slope and \(y\)-intercept.

A line has equation \(\displaystyle{ 6x+9y=5 }\text{.}\)

This lineā€™s slope is .

This lineā€™s \(y\)-intercept is .

30.

Find the lineā€™s slope and \(y\)-intercept.

A line has equation \(\displaystyle{ 6x+8y=3 }\text{.}\)

This lineā€™s slope is .

This lineā€™s \(y\)-intercept is .

31.

Fill out this table for the equation \(x=-5\text{.}\) The first row is an example.

\(x\) \(y\) Points
\(-5\) \(-3\) \(\left(-5,-3\right)\)
\(-2\)
\(-1\)
\(0\)
\(1\)
\(2\)
32.

Fill out this table for the equation \(x=-4\text{.}\) The first row is an example.

\(x\) \(y\) Points
\(-4\) \(-3\) \(\left(-4,-3\right)\)
\(-2\)
\(-1\)
\(0\)
\(1\)
\(2\)
33.

A lineā€™s graph is shown. Write an equation for the line.

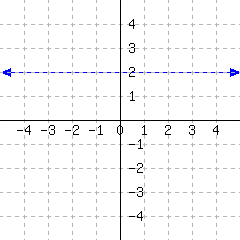
34.

A lineā€™s graph is shown. Write an equation for the line.

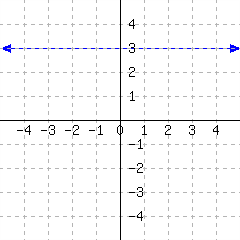
35.

Line \(m\) passes points \((10,0)\) and \((10,4)\text{.}\)

Line \(n\) passes points \((4,-3)\) and \((4,-2)\text{.}\)

These two lines are

  • parallel

  • perpendicular

  • neither parallel nor perpendicular

.

36.

Line \(m\) passes points \((-9,-7)\) and \((-9,-9)\text{.}\)

Line \(n\) passes points \((-2,-3)\) and \((-2,9)\text{.}\)

These two lines are

  • parallel

  • perpendicular

  • neither parallel nor perpendicular

.