ORCCA Functions and their Representations Chapter Review

Section 10.5 Functions and their Representations Chapter Review

Subsection 10.5.1 Function Basics

In Section 10.1 we defined functions 10.1.2 informally, as well as function notation 10.1.6. We saw functions in four forms 10.1.30: verbal descriptions, formulas, graphs and tables.

Example 10.5.1. Informal Definition of a Function.

Determine whether each example below describes a function.

The area of a circle given its radius.
The number you square to get $9\text{.}$

Explanation

The area of a circle given its radius is a function because there is a set of steps or a formula that changes the radius into the area of the circle. We could write $A(r)=\pi r^2\text{.}$
The number you square to get $9$ is not a function because the process we would apply to get the result does not give a single answer. There are two different answers, $-3$ and $3\text{.}$ A function must give a single output for a given input.

Example 10.5.2. Tables and Graphs.

Make a table and a graph of the function $f\text{,}$ where $f(x)=x^2\text{.}$

Explanation

First we will set up a table with negative and positive inputs and calculate the function values. The values are shown in Table 10.5.3, which in turn gives us the graph in Figure 10.5.4.

Table 10.5.3.

input, $x$	output, $\operatorname{f}(x)$
$-3$	$9$
$-2$	$4$
$-1$	$1$
$0$	$0$
$1$	$2$
$2$	$4$
$3$	$9$

a graph of the points from the table connected with a dashed line — Figure 10.5.4. $y=f(x)=x^2$

Example 10.5.5. Translating between Four Descriptions of the Same Function.

Consider a function $f$ that triples its input and then adds $4\text{.}$ Translate this verbal description of $f$ into a table, a graph, and a formula.

Explanation

To make a table for $f\text{,}$ we'll have to select some input $x$-values so we will choose some small negative and positive values that are easy to work with. Given the verbal description, we should be able to compute a column of output values. Table 10.5.6 is one possible table that we might end up with.

Table 10.5.6.

$x$	$f(x)$
$-2$	$3(-2)+4=-2$
$-1$	$3(-1)+4=1$
$0 $	$3(0)+4=4$
$1 $	$3(1)+4=7$
$2 $	$3(2)+4=10$

Once we have a table for $f\text{,}$ we can make a graph for $f$ as in Figure 10.5.7, using the table to plot points.

Lastly, we must find a formula for $f\text{.}$ This means we need to write an algebraic expression that says the same thing about $f$ as the verbal description, the table, and the graph. For this example, we can focus on the verbal description. Since $f$ takes its input, triples it, and adds $4\text{,}$ we have the formula

\begin{equation*} f(x)=3x+4\text{.} \end{equation*}

a graph of the points listed in the table; the points are connected with a dotted line and form a parabola — Figure 10.5.7. $y=f(x)$

Subsection 10.5.2 Domain and Range

In Section 10.2 we saw the definition of domain 10.2.5 and range 10.2.18, and three types of domain restrictions 10.2.17. We also learned how to write the domain and range in interval and set-builder notation.

Example 10.5.8. Domain.

Determine the domain of $p\text{,}$ where $p(x)=\dfrac{x}{2x-1}\text{.}$

Explanation

This is an example of the first type of domain restriction, when you have a variable in the denominator. The denominator cannot equal $0$ so a bad value for $x$ would be when

\begin{align*} 2x-1\amp=0\\ 2x\amp=1\\ x\amp=\frac{1}{2} \end{align*}

The domain is all real numbers except $\frac{1}{2}\text{.}$

Example 10.5.9. Interval, Set, and Set-Builder Notation.

What is the domain of the function $C\text{,}$ where $C(x)=\sqrt{2x-3}-5\text{?}$

Explanation

This is an example of the second type of domain restriction where the value inside the radical cannot be negative. So the good values for $x$ would be when

\begin{align*} 2x-3\amp\geq0\\ 2x\geq 3\\ x\geq \frac{3}{2} \end{align*}

So on a number line, if we wanted to picture the domain of $C\text{,}$ we would make a sketch like:

The domain is the interval $\left[\frac{3}{2},\infty\right)\text{.}$

Example 10.5.10. Range.

Find the range of the function $q$ using its graph shown in Figure 10.5.11.

Figure 10.5.11. $y=q(x)\text{.}$ The range is marked as an interval on the $y$-axis.

Explanation

The range is the collection of possible numbers that $q$ can give for output. Figure 10.5.11 displays a graph of $q\text{,}$ with the range shown as an interval on the $y$-axis.

The output values are the $y$-coordinates so we can see that the $y$-values start from $1$ and continue downward forever. Therefore the range is $(-\infty,1]\text{.}$

Subsection 10.5.3 Simplifying Expressions with Function Notation

In Section 10.3 we learned about the difference between $f(-x)$ and $-f(x)$ and how to simplify them. We also learned how to simplify other changes to the input and output like $f(3x)$ and $\frac{1}{3}f(x)\text{.}$ Here are some examples.

Example 10.5.12. Negative Signs in and out of Function Notation.

Find and simplify a formula for $f(-x)$ and $-f(x)\text{,}$ where $f(x)=-3x^2-7x+1\text{.}$

Explanation

To find $f(-x)\text{,}$ we use an input of $-x$ in our function $f$ and simplify to get:

\begin{align*} f(\substitute{-x})\amp=-3(\substitute{-x})^2-7(\substitute{-x})+1\\ \amp=-3x^2+7x+1 \end{align*}

To find $-f(x)\text{,}$ we take the opposite of the function $f$ and simplify to get:

\begin{align*} \highlight{-}f(x)\amp=\highlight{-}(-3x^2-7x+1)\\ \amp=3x^2+7x-1 \end{align*}

Example 10.5.13. Other Nontrivial Simplifications.

If $g(x)=2x^2-3x-5\text{,}$ find and simplify a formula for $g(x-1)\text{.}$

Explanation

To find $g(x-1)\text{,}$ we put in $(x-1)$ for the input. It is important to keep the parentheses because we have exponents and negative signs in the function.

\begin{align*} g(\substitute{x-1})\amp=2(\substitute{x-1})^2-3(\substitute{x-1})-5\\ \amp=2(x^2-2x+1)-3x+3-5\\ \amp=2x^2-4x+2-3x-2\\ \amp=2x^2-7x \end{align*}

Subsection 10.5.4 Technical Definition of a Function

In Section 10.4 we gave a formal definition of a function 10.4.1 and learned to identify what is and is not a function with sets or ordered pairs, tables and graphs. We also used the vertical line test 10.4.18.

Example 10.5.14. Formally Defining a Function.

We learned that sets of ordered pairs, tables and graphs can meet the formal definition of a function. Here is an example that shows a function in all three forms. We can verify that each input has at most one output.

The function $f$ represented as a collection of ordered pairs.

\begin{equation*} \{(1,4),(2,4),(3,3),(4,6),(5,-2)\} \end{equation*}

$x$	$f(x)$
$1$	$4$
$2$	$4$
$3$	$3$
$4$	$6$
$5$	$-2$

Figure 10.5.15. The function $f$ represented as a table.

Figure 10.5.16. The function $f$ represented as a graph.

Example 10.5.17. Identifying What is Not a Function.

Identify whether each graph represents a function using the vertical line test 10.4.18.

Figure 10.5.18.

Figure 10.5.19.

Figure 10.5.20.

Explanation

Figure 10.5.21. A vertical line touching the graph twice makes this graph not give $y$ as a function of $x\text{.}$

Figure 10.5.22. A vertical line touching the graph twice makes this graph not give $y$ as a function of $x\text{.}$

Figure 10.5.23. All vertical lines only touch the graph once, so this graph does give $y$ as a function of $x\text{.}$

Exercises 10.5.5 Exercises

Function Basics

1.

Evaluate the function at the given values.

$\displaystyle{G(x)={\frac{4}{x+7}}}$ .

$\displaystyle{G(-11)=}$ .
$\displaystyle{G(-7)=}$ .

2.

Evaluate the function at the given values.

$\displaystyle{G(x)={-\frac{40}{x+1}}}$ .

$\displaystyle{G(4)=}$ .
$\displaystyle{G(-1)=}$ .

3.

Use the graph of $H$ below to evaluate the given expressions. (Estimates are OK.)

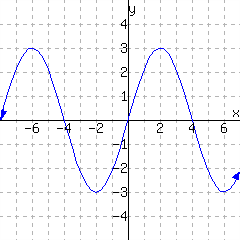
$H(-6)={}$
$H(4)={}$

4.

Use the graph of $K$ below to evaluate the given expressions. (Estimates are OK.)

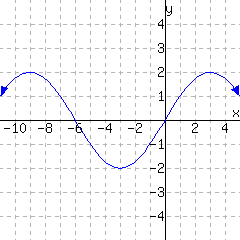
$K(-9)={}$
$K(0)={}$

5.

Use the graph of $f$ below to evaluate the given expressions. (Estimates are OK.)

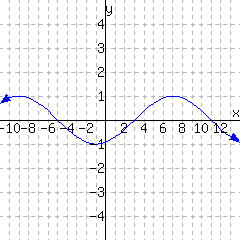
$f(-9)={}$
$f(11)={}$

6.

Use the graph of $f$ below to evaluate the given expressions. (Estimates are OK.)

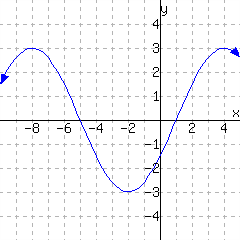
$f(-8)={}$
$f(1)={}$

7.

Use the table of values for $g$ below to evaluate the given expressions.

$x$	$0$	$2$	$4$	$6$	$8$
$g(x)$	$0.2$	$7.2$	$6.3$	$-1.1$	$9.4$

$g({0})={}$
$g({6})={}$

8.

Use the table of values for $h$ below to evaluate the given expressions.

$x$	$-1$	$0$	$1$	$2$	$3$
$h(x)$	$8.9$	$7$	$0.2$	$0$	$2.2$

$h({0})={}$
$h({3})={}$

9.

Make a table of values for the function $K\text{,}$ defined by $K(x)={-2x^{2}}\text{.}$ Based on values in the table, sketch a graph of $K\text{.}$

$x$	$K(x)$

10.

Make a table of values for the function $h\text{,}$ defined by $\displaystyle h(x)={\frac{2^{x}+2}{x^{2}+3}}\text{.}$ Based on values in the table, sketch a graph of $h\text{.}$

$x$	$h(x)$

11.

Joseph will spend ${\$240}$ to purchase some bowls and some plates. Each plate costs ${\$1}\text{,}$ and each bowl costs ${\$6}\text{.}$ The function $q(x)={-{\frac{1}{6}}x+40}$ models the number of bowls Joseph will purchase, where $x$ represents the number of plates to be purchased.

Interpret the meaning of $q(30)={35}\text{.}$

A. $35$ plates and $30$ bowls can be purchased.
B. $\$35$ will be used to purchase bowls, and $\$30$ will be used to purchase plates.
C. $\$30$ will be used to purchase bowls, and $\$35$ will be used to purchase plates.
D. $30$ plates and $35$ bowls can be purchased.

12.

Charity will spend ${\$450}$ to purchase some bowls and some plates. Each plate costs ${\$7}\text{,}$ and each bowl costs ${\$9}\text{.}$ The function $q(x)={-{\frac{7}{9}}x+50}$ models the number of bowls Charity will purchase, where $x$ represents the number of plates to be purchased.

Interpret the meaning of $q(36)={22}\text{.}$

A. $22$ plates and $36$ bowls can be purchased.
B. $\$22$ will be used to purchase bowls, and $\$36$ will be used to purchase plates.
C. $\$36$ will be used to purchase bowls, and $\$22$ will be used to purchase plates.
D. $36$ plates and $22$ bowls can be purchased.

13.

The following figure has the graph $y=d(t)\text{,}$ which models a particle’s distance from the starting line in feet, where $t$ stands for time in seconds since timing started.

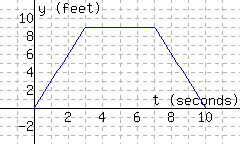
Find $d(9)\text{.}$
Interpret the meaning of $d(9)\text{.}$
- A. The particle was $3$ feet away from the starting line $9$ seconds since timing started.
- B. In the first $9$ seconds, the particle moved a total of $3$ feet.
- C. In the first $3$ seconds, the particle moved a total of $9$ feet.
- D. The particle was $9$ feet away from the starting line $3$ seconds since timing started.
Solve $d(t)={6}$ for $t\text{.}$ $t=$
Interpret the meaning of part c’s solution(s).
- A. The particle was $6$ feet from the starting line $2$ seconds since timing started, or $8$ seconds since timing started.
- B. The particle was $6$ feet from the starting line $8$ seconds since timing started.
- C. The particle was $6$ feet from the starting line $2$ seconds since timing started.
- D. The particle was $6$ feet from the starting line $2$ seconds since timing started, and again $8$ seconds since timing started.

14.

The following figure has the graph $y=d(t)\text{,}$ which models a particle’s distance from the starting line in feet, where $t$ stands for time in seconds since timing started.

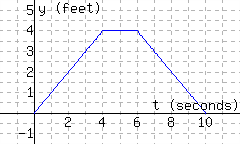
Find $d(6)\text{.}$
Interpret the meaning of $d(6)\text{.}$
- A. In the first $6$ seconds, the particle moved a total of $4$ feet.
- B. The particle was $6$ feet away from the starting line $4$ seconds since timing started.
- C. In the first $4$ seconds, the particle moved a total of $6$ feet.
- D. The particle was $4$ feet away from the starting line $6$ seconds since timing started.
Solve $d(t)={1}$ for $t\text{.}$ $t=$
Interpret the meaning of part c’s solution(s).
- A. The particle was $1$ feet from the starting line $9$ seconds since timing started.
- B. The particle was $1$ feet from the starting line $1$ seconds since timing started, or $9$ seconds since timing started.
- C. The particle was $1$ feet from the starting line $1$ seconds since timing started, and again $9$ seconds since timing started.
- D. The particle was $1$ feet from the starting line $1$ seconds since timing started.

Domain and Range

15.

A function is graphed.

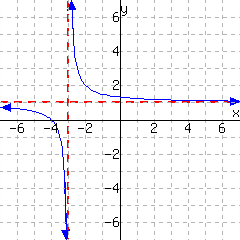
This function has domain and range .

16.

A function is graphed.

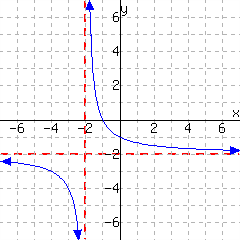
This function has domain and range .

17.

A function is graphed.

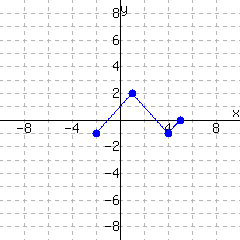
The function has domain and range .

18.

A function is graphed.

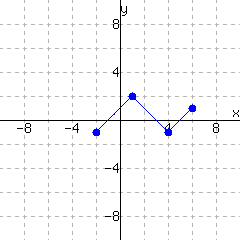
The function has domain and range .

19.

A function is graphed.

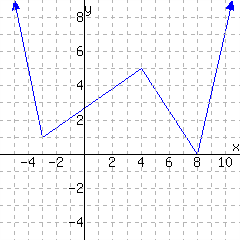
The function has domain and range .

20.

A function is graphed.

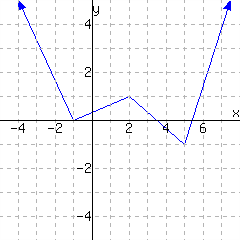
The function has domain and range .

21.

An object was shot up into the air at an initial vertical speed of $576$ feet per second. Its height as time passes can be modeled by the quadratic function $f\text{,}$ where $f(t)={-16t^{2}+576t}\text{.}$ Here $t$ represents the number of seconds since the object’s release, and $f(t)$ represents the object’s height in feet.

Find the function’s domain and range in this context.

The function’s domain in this context is .

The function’s range in this context is .

22.

An object was shot up into the air at an initial vertical speed of $608$ feet per second. Its height as time passes can be modeled by the quadratic function $f\text{,}$ where $f(t)={-16t^{2}+608t}\text{.}$ Here $t$ represents the number of seconds since the object’s release, and $f(t)$ represents the object’s height in feet.

Find the function’s domain and range in this context.

The function’s domain in this context is .

The function’s range in this context is .

23.

Find the domain of $c$ where $\displaystyle{c(x)= \frac{\sqrt{1 + x}}{9 - x}}\text{.}$

24.

Find the domain of $p$ where $\displaystyle{p(x)= \frac{\sqrt{3 + x}}{5 - x}}\text{.}$

25.

Find the domain of $a$ where $\displaystyle{a(x)= \frac{\sqrt{5 + x}}{2 - x}}\text{.}$

26.

Find the domain of $m$ where $\displaystyle{m(x)= \frac{\sqrt{7 + x}}{8 - x}}\text{.}$

Simplifying Expressions with Function Notation

27.

Simplify $F(y)+2\text{,}$ where $F(y)={2+2.3y}\text{.}$

28.

Simplify $f(r)+5\text{,}$ where $f(r)={-6-2.2r}\text{.}$

29.

Let $f$ be a function given by $f(x)={4x^{2}+5x}\text{.}$ Find and simplify the following:

$f(x) - 5={}$
$f(x - 5)={}$
$-5f(x)={}$
$f(-5x)={}$

30.

Let $f$ be a function given by $f(x)={-5x^{2}-x}\text{.}$ Find and simplify the following:

$f(x) - 2={}$
$f(x - 2)={}$
$-2f(x)={}$
$f(-2x)={}$

Technical Definition of a Function

31.

Does the following set of ordered pairs make for a function of $x\text{?}$

$\Big\{(9,7),(7,3),(-8,9),(7,9),(3,8)\Big\}$

This set of ordered pairs

describes
does not describe

a function of $x\text{.}$ This set of ordered pairs has domain and range .

32.

Does the following set of ordered pairs make for a function of $x\text{?}$

$\Big\{(2,8),(-9,8),(6,9),(6,10),(-9,7)\Big\}$

This set of ordered pairs

describes
does not describe

a function of $x\text{.}$ This set of ordered pairs has domain and range .

33.

Below is all of the information that exists about a function $f\text{.}$

$\begin{aligned} f(0)\amp =5\amp f(2)\amp =2\amp f(4)\amp =1 \end{aligned}$

Write $f$ as a set of ordered pairs.

$f$ has domain and range .

34.

Below is all of the information about a function $g\text{.}$

$\begin{aligned} g(a)\amp =1\amp g(b)\amp =-3\\ g(c)\amp =2\amp g(d)\amp =-3 \end{aligned}$

Write $g$ as a set of ordered pairs.

$g$ has domain and range .

35.

The following graphs show two relationships. Decide whether each graph shows a relationship where $y$ is a function of $x\text{.}$

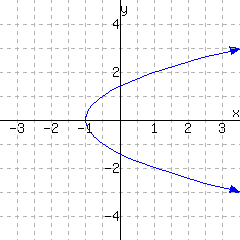
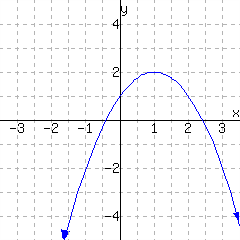
The first graph

does
does not

give a function of $x\text{.}$ The second graph

does
does not

give a function of $x\text{.}$

36.

The following graphs show two relationships. Decide whether each graph shows a relationship where $y$ is a function of $x\text{.}$

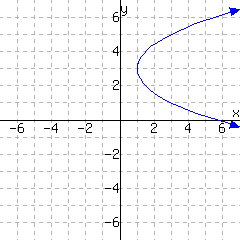
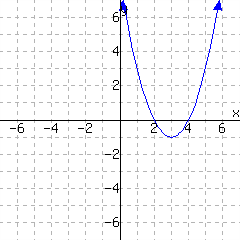
The first graph

does
does not

give a function of $x\text{.}$ The second graph

does
does not

give a function of $x\text{.}$

37.

Determine whether or not each of the following tables could be the table of values of a function. If the table can not be the table of values of a function, give an input that has more than one possible output.

Input	Output
$2$	$3$
$4$	$19$
$6$	$3$
$8$	$15$
$-2$	$-5$

Could this be the table of values for a function?

If not, which input has more than one possible output?

-2
2
4
6
8
None, the table could be the table of values of a function.

Input	Output
$-4$	$4$
$-3$	$5$
$-2$	$-15$
$-3$	$16$
$-1$	$10$

Could this be the table of values for a function?

If not, which input has more than one possible output?

-4
-3
-2
-1
None, the table could be the table of values of a function.

38.

Input	Output
$2$	$7$
$4$	$5$
$6$	$7$
$8$	$4$
$-2$	$-6$

Could this be the table of values for a function?

If not, which input has more than one possible output?

-2
2
4
6
8
None, the table could be the table of values of a function.

Input	Output
$-4$	$-16$
$-3$	$7$
$-2$	$2$
$-3$	$22$
$-1$	$-12$

Could this be the table of values for a function?

If not, which input has more than one possible output?

-4
-3
-2
-1
None, the table could be the table of values of a function.

input, \(x\)	output, \(\operatorname{f}(x)\)
\(-3\)	\(9\)
\(-2\)	\(4\)
\(-1\)	\(1\)
\(0\)	\(0\)
\(1\)	\(2\)
\(2\)	\(4\)
\(3\)	\(9\)

\(x\)	\(f(x)\)
\(-2\)	\(3(-2)+4=-2\)
\(-1\)	\(3(-1)+4=1\)
\(0 \)	\(3(0)+4=4\)
\(1 \)	\(3(1)+4=7\)
\(2 \)	\(3(2)+4=10\)

\(x\)	\(f(x)\)
\(1\)	\(4\)
\(2\)	\(4\)
\(3\)	\(3\)
\(4\)	\(6\)
\(5\)	\(-2\)

\(x\)	\(0\)	\(2\)	\(4\)	\(6\)	\(8\)
\(g(x)\)	\(0.2\)	\(7.2\)	\(6.3\)	\(-1.1\)	\(9.4\)

\(x\)	\(-1\)	\(0\)	\(1\)	\(2\)	\(3\)
\(h(x)\)	\(8.9\)	\(7\)	\(0.2\)	\(0\)	\(2.2\)

\(x\)	\(K(x)\)