Section 7.7 Solving Quadratic Equations by Factoring
Subsection 7.7.1 Quadratic Equations and the Zero Product Property
We have learned how to factor trinomials like \(x^2+5x+6\) into \((x+2)(x+3)\text{.}\) This skill is needed to solve an equation like \(x^2+5x+6=0\text{,}\) which is a quadratic equation. A quadratic equation is is an equation in the form \(ax^2+bx+c=0\) with \(a\neq0\text{.}\) We also consider equations such as \(x^2=x+3\) and \(5x^2+3= (x+1)^2 + (x + 1)(x-3)\) to be quadratic equations, because we can expand any multiplication, add or subtract terms from both sides, and combine like terms to get the form \(ax^2+bx+c=0\text{.}\) The form \(ax^2+bx+c=0\) is called the standard form of a quadratic equation.
Before we begin exploring the method of solving quadratic equations by factoring, we'll identify what types of equations are quadratic and which are not.
Checkpoint 7.7.1.
Now we'll look at an application that demonstrates the need and method for solving a quadratic equation by factoring.
Nita is in a physics class that launches a tennis ball from a rooftop \(80\) feet above the ground. They fire it upward, but at an angle, at a speed of \(64\) feet per second and measure the time it takes for the ball to hit the ground below. We can model the height of the tennis ball, \(h\text{,}\) in feet, with the quadratic equation
where \(t\) represents the time in seconds after the launch. Using the model we can predict when the ball will hit the ground.
The ground has a height of \(0\text{,}\) or \(h=0\text{.}\) We will substitute \(0\) for \(h\) in the equation and we have
We need to solve this quadratic equation for \(t\) to find when the ball will hit the ground.
The key strategy for solving a linear equation is to separate the variable terms from the constant terms on either side of the equal sign. It turns out that this same method will not work for quadratic equations. Fortunately, we already have spent a good amount of time discussing a method that will work: factoring. If we can factor the polynomial on the left-hand side, we will be on the home stretch to solving the whole equation.
We will look for a common factor first, and see that we can factor out \(-16\text{.}\) Then we can finish factoring the trinomial:
In order to finish solving the equation, we need to understand the following property. This property explains why it was incredibly important to \(not\) move the \(80\) in our example over to the other side of the equation before trying to factor.
Fact 7.7.3. Zero Product Property.
If the product of two or more numbers is equal to zero, then at least one of the numbers must be zero.
One way to understand this property is to think about the equation \(a\cdot b=0\text{.}\) Maybe \(b=0\text{,}\) because that would certainly cause the equation to be true. But suppose that \(b\neq0\text{.}\) Then it is safe to divide both sides by \(b\text{,}\) and the resulting equation says that \(a=0\text{.}\) So no matter what, either \(a=0\) or \(b=0\text{.}\)
To understand this property more, let's look at a few products:
When none of the factors are \(0\text{,}\) the result is never \(0\text{.}\) The only way to get a product of \(0\) is when one of the factors is \(0\text{.}\) This property is unique to the number \(0\) and can be used no matter how many numbers are multiplied together.
Now we can see the value of factoring. We have three factors in our equation
The first factor is the number \(-16\text{.}\) The second and third factors, \(t+1\) and \(t-5\text{,}\) are expressions that represent numbers. Since the product of the three factors is equal to \(0\text{,}\) one of the factors must be zero.
Since \(-16\) is not \(0\text{,}\) either \(t+1\) or \(t-5\) must be \(0\text{.}\) This gives us two equations to solve:
We have found two solutions, \(-1\) and \(5\text{.}\) A quadratic expression will have at most two linear factors, not including any constants, so it can have up to two solutions.
Let's check each of our two solutions \(-1\) and \(5\text{:}\)
We have verified our solutions. While there are two solutions to the equation, the solution \(-1\) is not relevant to this physics model because it is a negative time, which would tell us something about the ball's height before it was launched. The solution \(5\) does make sense. According to the model, the tennis ball will hit the ground \(5\) seconds after it is launched.
Subsection 7.7.2 Further Examples
We'll now look at further examples of solving quadratic equations by factoring. The general process is outlined here:
Process 7.7.4. Solving Quadratic Equations by Factoring.
- Simplify
Simplify the equation using distribution and by combining like terms.
- Isolate
Move all terms onto one side of the equation so that the other side has \(0\text{.}\)
- Factor
Factor the quadratic expression.
- Apply the Zero Product Property
Apply the Zero Product Property.
- Solve
Example 7.7.5.
Solve \(x^2-5x-14=0\) by factoring.
The solutions are \(-2\) and \(7\text{,}\) so the solution set is written as \(\{-2, 7\}\text{.}\)
If the two factors of a polynomial happen to be the same, the equation will only have one solution. Let's look at an example of that.
Example 7.7.6. A Quadratic Equation with Only One Solution.
Solve \(x^2-10x+25=0\) by factoring.
The solution is \(5\text{,}\) so the solution set is written as \(\{5\}\text{.}\)
Example 7.7.7. Factor Out a Common Factor.
Solve \(5x^2+55x+120=0\) by factoring.
Note that the terms are all divisible by \(5\text{,}\) so we can factor that out to start.
The solution set is \(\{-8, -3\}\text{.}\)
Example 7.7.8. Factoring Using the AC Method.
Solve \(3x^2-7x+2=0\) by factoring.
Recall that we multiply \(3\cdot2=6\) and find a factor pair that multiplies to \(6\) and adds to \(-7\text{.}\) The factors are \(-6\) and \(-1\text{.}\) We use the two factors to replace the middle term with \(-6x\) and \(-x\text{.}\)
The solution set is \(\left\{\frac{1}{3}, 2\right\}\text{.}\)
Try a similar exercise.
Checkpoint 7.7.9.
So far the equations have been written in standard form, which is
If an equation is not given in standard form then we must rearrange it in order to use the Zero Product Property.
Example 7.7.10. Writing in Standard Form.
Solve \(x^2-10x=24\) by factoring.
There is nothing like the Zero Product Property for the number \(24\text{.}\) We must have a \(0\) on one side of the equation to solve quadratic equations using factoring.
The solution set is \(\{-2, 12\}\text{.}\)
Example 7.7.11. Writing in Standard Form.
Solve \((x+4)(x-3)=18\) by factoring.
Again, there is nothing like the Zero Product Property for a number like \(18\text{.}\) We must expand the left side and subtract \(18\) from both sides.
The solution set is \(\{-6, 5\}\text{.}\)
Example 7.7.12. A Quadratic Equation with No Constant Term.
Solve \(2x^2=5x\) by factoring.
It may be tempting to divide both sides of the equation by \(x\text{.}\) But \(x\) is a variable, and for all we know, maybe \(x=0\text{.}\) So it is not safe to divide by \(x\text{.}\) As a general rule, never divide an equation by a variable in the solving process. Instead, we will put the equation in standard form.
We can factor out \(x\text{.}\)
\begin{align*} x(2x-5)\amp=0 \end{align*}The solution set is \(\left\{0, \frac{5}{2}\right\}\text{.}\) In general, if a quadratic equation does not have a constant term, then \(0\) will be one of the solutions.
Example 7.7.13. Factoring a Special Polynomial.
Solve \(x^2=9\) by factoring.
We can put the equation in standard form and use factoring. In this case, we find a difference of squares.
The solution set is \(\{-3, 3\}\text{.}\)
Example 7.7.14. Solving an Equation with a Higher Degree.
Solve \(2x^3-10x^2-28x=0\) by factoring.
Although this equation is not quadratic, it does factor so we can solve it by factoring.
The solution set is \(\{-2, 0, 7\}\text{.}\)
Subsection 7.7.3 Applications
Example 7.7.15. Throwing a Ball.
A ball is thrown upward and follows a parabolic path modeled by the equation \(h=-16t^2+80t+6\text{,}\) where \(h\) represents the height of the ball, in feet, \(t\) seconds after it has been thrown. How long will it take for the ball to reach a height of \(70\) feet?
To solve this problem, we start by replacing the \(h\) in the equation with \(70\text{:}\)
This gives us a quadratic equation to solve. The first step to solve this equation is to get the equation into standard form by subtracting \(70\) from both sides to get zero on one side. Then, we can factor the other side and apply the zero product property.
Thus, there are two times at which the ball will reach a height of \(70\) feet. The ball will reach a height of \(70\) feet \(1\) second after it has been thrown and again \(4\) seconds after it has been thrown.
Example 7.7.16. Kicking it on Mars.
Some time in the recent past, Filip traveled to Mars for a vacation with his kids, Henrik and Karina, who wanted to kick a soccer ball around in the comparatively reduced gravity. Karina stood at point \(K\) and kicked the ball over her dad standing at point \(F\) to Henrik standing at point \(H\text{.}\) The height of the ball off the ground, \(h\) in feet, can be modeled by the equation \(h=-0.01\left(x^2-70x-1800\right)\text{,}\) where \(x\) is how far to the right the ball is from Filip. Note that distances to the left of Filip will be negative.
Find out how high the ball was above the ground when it passed over Filip's head.
Find the distance from Karina to Henrik.
-
The ball was neither left nor right of Filip when it went over him, so \(x=0\text{.}\) Plugging that value into our equation for \(x\text{,}\)
\begin{align*} h\amp=-0.01\left(0^2-70(0)-1800\right)\\ \amp=-0.01(-1800)\\ \amp=18 \end{align*}It seems that the soccer ball was \(18\) feet above the ground when it flew over Filip.
-
The distance from Karina to Henrik is the same as the distance from point \(K\) to point \(H\text{.}\) Also, the distances from \(K\) to point \(F\) and from point \(F\) to point \(H\) are associated with the values of \(x\) in the given formula that will give a height of zero: \(h=-0.01\left(x^2-70x-1800\right)\text{.}\) So to find these values, set \(h=0\) and solve for \(x\text{.}\)
\begin{align*} 0=-0.01\left(x^2-70x-1800\right)\\ \end{align*}Note that we can divide by \(-0.01\) on both sides of the equation to simplify.
\begin{align*} 0\amp=x^2-70x-1800\\ 0\amp=(x-90)(x+20)\\ \end{align*}So, either:
\begin{align*} x-90\amp=0\amp\text{or}\amp\amp x+20\amp=0\\ x\amp=90\amp\text{or}\amp\amp x\amp=-20 \end{align*}Since the \(x\)-values are how far right or left the points are from Filip, Karina is standing \(20\) feet left of Filip and Henrik is standing \(90\) feet right of Filip. Thus, the two kids are \(110\) feet apart.
It is worth noting that if this same kick, with same initial force at the same angle, took place on Earth, the ball would have traveled less than \(30\) feet from Karina before landing!
Next, we will look at an example involving right triangles. Right triangles have an important property called the Pythagorean Theorem.
Theorem 7.7.19. The Pythagorean Theorem.
For any right triangle, the lengths of the three sides have the following relationship: \(a^2+b^2=c^2\text{.}\) The sides \(a\) and \(b\) are called legs and the longest side \(c\) is called the hypotenuse.
Example 7.7.21. Pythagorean Theorem Application.
Justine wants to put a deck in the corner of her backyard in the shape of a right triangle, as shown below. The hypotenuse will be \(17\) feet long. The length of one side will be \(7\) feet shorter than the length of the other side. Find the lengths of the sides of the deck.
Since her deck is a right triangle, we know the Pythagorean Theorem must hold. So, we can substitute \(17\) in for \(c\text{,}\) in the Pythagorean Theorem, and \(x\) and \(x-7\) in for the lengths of the two legs \(a\) and \(b\text{.}\) This will give us:
Simplify both sides:
As you can see, this is a quadratic equation. So, we will solve this equation by factoring. First, we'll need to get it into standard form and then we can use the Zero Product Property.
Of course, a negative length doesn't make sense, so we'll ignore the negative solution. Thus, one side should be \(15\) feet long and the other side, which needs to be \(7\) feet shorter than that, should be \(8\) feet long.
Try a similar exercise.
Checkpoint 7.7.23.
Example 7.7.24. An Area Application.
Rajesh has a hot tub and he wants to build a deck of uniform width around it. The hot tub is 7 ft by 5 ft and it is covered by a rectangular roof that is 99 ft2. How wide can he make the deck so that it will be covered by the roof?
We will define \(x\) to represent the width of the deck (in feet). Here is a diagram to help us understand the scenario.
The overall length is \(7+2x\) feet, because Rajesh is adding \(x\) feet on each side. Similarly, the overall width is \(5+2x\) feet.
The formula for the area of a rectangle is \(\text{area}=\text{length}\cdot\text{width}\text{.}\) Since the total area of the roof is 99 ft2, we can write and solve the equation:
Since a length cannot be negative, we take \(x=2\) as the only applicable solution. Rajesh should make the deck 2 ft wide on each side to fit under the roof.
Subsection 7.7.4 Graphing a Quadratic Equation
Yet another application of solving quadratic equations is to graph equations of the form \(y=ax^2+bx+c\text{.}\) In Chapter 4, we learned how to find the \(x\)- and \(y\)-intercepts of a line. Here, we will learn that finding the \(x\)- and \(y\)-intercepts of the graph of any equation in two variables involves the same first step, due to the definition of those key points. This can help us graph many equations, including quadratic equations, which we will begin to explore in this section.
The graph of a quadratic equation of the form \(y=ax^2+bx+c\) has the shape of a parabola, like the one shown below.
Below is the graph of \(y=x^2-3x+2\text{.}\) This parabola opens upward, but some parabolas will open downward. Whether a parabola will open upward or downward depends on the sign of \(a\text{,}\) the coefficient of \(x^2\text{.}\) If \(a>0\text{,}\) then the parabola will open upward. On the other hand, if \(a<0\text{,}\) then the parabola will open downward.
To find the \(x\)- and \(y\)-intercepts of the graph of \(y=ax^2+bx+c\text{,}\) we follow the same steps as we do with linear equations. That is, to find the \(y\)-intercept, we plug in \(0\) for \(x\) and then solve for \(y\text{,}\) and to find the \(x\)-intercept(s), we plug in \(0\) for \(y\) and then solve for \(x\text{.}\) The latter will involve solving a quadratic equation, which will call for your newly acquired solving-by-factoring skills.
Another key point that will help us graph our parabola is the minimum point, if it's opening upward, or the maximum point, if it's opening downward. This key pont is called the vertex of the parabola.
Fact 7.7.27.
If we let \((h,k)\) denote the coordinates of the vertex of a parabola whose equation is \(y=ax^2+bx+c\text{,}\) then \(h=-\frac{b}{2a}\text{.}\) and \(k=ah^2+bh+c\text{.}\)
Note that the formula for finding \(k\) is simply the result of plugging the value you find for \(h\) into the equation for the parabola, \(y=ax^2+bx+c\text{.}\) This will give you the \(y\)-coordinate of the vertex, which is denoted by \(k\text{.}\) So, there is no need to memorize that formula.
We can find additional points, to get a more accurate sketch of our parabola, by plugging additional values in for \(x\) and solving for \(y\text{,}\) much the same as we did to graph lines.
Example 7.7.28. Graphing a Parabola.
Graph the equation \(y=x^2-4x-12\) by finding the vertex, the \(x\)- and \(y\)-intercepts, and any additional points necessary to make a nice parabola.
First, notice that \(a=1\text{,}\) which is more than zero, so we know the parabola will be opening upward. Next, we can use the formula, given in Fact 7.7.27 to find the vertex, where \(a=1\) and \(b=-4\text{:}\)
Now, we can substitute \(h=2\) into the equation to find \(k\text{:}\)
Thus, the vertex of the parabola is the point \((2,-16)\text{.}\)
To find the \(y\)-intercept, we plug in \(0\) for \(x\) and solve for \(y\text{:}\)
Hence, the \(y\)-intercept of the parabola is the point \((0,-12)\text{.}\)
To find the \(x\)-intercept(s), we plug in \(0\) for \(y\) and solve for \(x\text{,}\) which we will do by factoring:
Therefore, there are two \(x\)-intercepts: \((6,0)\) and \((-2,0)\text{.}\)
So far, we have points with \(x\)-coordinates of \(-2\text{,}\) \(0\text{,}\) \(2\text{,}\) and \(6\text{.}\) To make a full graph, we can choose more values of \(x\) to plug into the equation and then solve for \(y\text{.}\) This will give us additional points to plot. It's helpful to organize this work in a table, like we did when we graphed lines.
| \(x\) | \(y=x^2-4x-12\) | Point |
| \(1\) | \((1)^2-4(1)-12=-15\) | \((1,-15)\) |
| \(3\) | \((3)^2-4(3)-12=-15\) | \((3,-15)\) |
| \(4\) | \((4)^2-4(4)-12=-12\) | \((4,-12)\) |
Plotting all the points we found and connecting them with a smooth curve gives us the following graph:
Example 7.7.31.
Graph the equation \(y=-2x^2+8x-6\) by finding the vertex, the \(x\)- and \(y\)-intercepts, and any additional points necessary to make a nice parabola.
First, notice that \(a=-2\text{,}\) which is less than zero, so we know the parabola will be opening downward. Next, we can use the formula, given in Fact 7.7.27 to find the vertex, where \(a=-2\) and \(b=8\text{:}\)
Now, we can substitute \(h=2\) into the equation to find \(k\text{:}\)
Thus, the vertex of the parabola is the point \((2,2)\text{.}\)
To find the \(y\)-intercept, we plug in \(0\) for \(x\) and solve for \(y\text{:}\)
Hence, the \(y\)-intercept of the parabola is the point \((0,-6)\text{.}\)
To find the \(x\)-intercept(s), we plug in \(0\) for \(y\) and solve for \(x\text{,}\) which we will do by factoring:
Therefore, there are two \(x\)-intercepts: \((3,0)\) and \((1,0)\text{.}\)
So far, we have points with \(x\)-coordinates of \(0\text{,}\) \(1\text{,}\) \(2\text{,}\) and \(3\text{.}\) To make a full graph, we can choose more values of \(x\) to plug into the equation and then solve for \(y\text{.}\) This will give us additional points to plot. It's helpful to organize this work in a table, like we did when we graphed lines.
| \(x\) | \(y=-2x^2+8x-6\) | Point |
| \(-1\) | \(-2(-1)^2+8(-1)-6=-16\) | \((-1,-16)\) |
| \(4\) | \(-2(4)^2+8(4)-6=-6\) | \((4,-6)\) |
| \(5\) | \(-2(5)^2+8(5)-6=-16\) | \((5,-16)\) |
Plotting all the points we found and connecting them with a smooth curve gives us the following graph:
Checkpoint 7.7.34.
Checkpoint 7.7.35.
Graph the parabola with the equation \(y=x^2-2x-15\) by algebraically finding its vertex and intercepts and any other additional points that you may find helpful.
Here is the answer to check. The algebra steps, however, are left to the reader.
The parabola opens upward.
The \(x\)-intercepts are \((-3,0)\) and \((5,0)\text{.}\)
The \(y\)-intercept is \((0,-15)\text{.}\)
The vertex is \((1,-16)\text{.}\)
An additional point that was found is \((2,-15)\text{.}\)
Exercises 7.7.5 Exercises
Warmup and Review
1.
Factor the given polynomial.
\(10r - 40=\)
2.
Factor the given polynomial.
\(7t+56=\)
3.
Factor the given polynomial.
\({t^{2}+2t-15}=\)
4.
Factor the given polynomial.
\({t^{2}+7t-30}=\)
5.
Factor the given polynomial.
\({3x^{2}-4x+1}=\)
6.
Factor the given polynomial.
\({2x^{2}-11x+9}=\)
7.
Factor the given polynomial.
\({18y^{2}+6y+54}=\)
8.
Factor the given polynomial.
\({20y^{2}-50y+50}=\)
9.
Factor the given polynomial.
\({9r^{4}-64}=\)
10.
Factor the given polynomial.
\({121r^{4}-49}=\)
Solve Quadratic Equations by Factoring
11.
Solve the equation.
\((x+6)(x - 1) = 0\)
12.
Solve the equation.
\((x+9)(x - 9) = 0\)
13.
Solve the equation.
\({90\!\left(x+10\right)\!\left(16x-5\right)} = 0\)
14.
Solve the equation.
\({98\!\left(x-9\right)\!\left(10x+1\right)} = 0\)
15.
Solve the equation.
\({x^{2}+3x+2} = 0\)
16.
Solve the equation.
\({x^{2}+12x+32} = 0\)
17.
Solve the equation.
\({x^{2}+2x-8} = 0\)
18.
Solve the equation.
\({x^{2}-4x-5} = 0\)
19.
Solve the equation.
\({x^{2}-6x+8} = 0\)
20.
Solve the equation.
\({x^{2}-10x+21} = 0\)
21.
Solve the equation.
\({x^{2}+19x} = {-90}\)
22.
Solve the equation.
\({x^{2}+17x} = {-70}\)
23.
Solve the equation.
\({x^{2}-5x} = {36}\)
24.
Solve the equation.
\({x^{2}+4x} = {60}\)
25.
Solve the equation.
\({x^{2}-11x} = {-28}\)
26.
Solve the equation.
\({x^{2}-14x} = {-48}\)
27.
Solve the equation.
\({x^{2}} = {-x}\)
28.
Solve the equation.
\({x^{2}} = {-3x}\)
29.
Solve the equation.
\({8x^{2}} = {48x}\)
30.
Solve the equation.
\({9x^{2}} = {-72x}\)
31.
Solve the equation.
\({10x^{2}} = {-7x}\)
32.
Solve the equation.
\({2x^{2}} = {7x}\)
33.
Solve the equation.
\({x^{2}-6x+9}=0\)
34.
Solve the equation.
\({x^{2}-8x+16}=0\)
35.
Solve the equation.
\({x^{2}}={10x-25}\)
36.
Solve the equation.
\({x^{2}}={14x-49}\)
37.
Solve the equation.
\({25x^{2}}={-10x-1}\)
38.
Solve the equation.
\({4x^{2}}={-28x-49}\)
39.
Solve the equation.
\({5x^{2}}={-24x-27}\)
40.
Solve the equation.
\({2x^{2}}={-27x-81}\)
41.
Solve the equation.
\({x^{2}-81} = 0\)
42.
Solve the equation.
\({x^{2}-49} = 0\)
43.
Solve the equation.
\({16x^{2}-25}=0\)
44.
Solve the equation.
\({25x^{2}-1}=0\)
45.
Solve the equation.
\({49x^{2}}={121}\)
46.
Solve the equation.
\({49x^{2}}={16}\)
47.
Solve the equation.
\({x\!\left(x-6\right)} = {72}\)
48.
Solve the equation.
\({x\!\left(x+1\right)} = {72}\)
49.
Solve the equation.
\({x\!\left(5x+44\right)}={60}\)
50.
Solve the equation.
\({x\!\left(4x+27\right)}={-18}\)
51.
Solve the equation.
\({\left(x+2\right)\!\left(x+2\right)} = {1}\)
52.
Solve the equation.
\({\left(x+3\right)\!\left(x-4\right)} = {8}\)
53.
Solve the equation.
\({\left(x+2\right)\!\left(4x-9\right)} = {2+3x^{2}}\)
54.
Solve the equation.
\({\left(x-1\right)\!\left(2x-1\right)} = {x^{2}-1}\)
55.
Solve the equation.
\({x\!\left(x+12\right)}={3\!\left(2x-3\right)}\)
56.
Solve the equation.
\({x\!\left(x+20\right)}={5\!\left(2x-5\right)}\)
57.
Solve the equation.
\({64x^{2}+112x+49}=0\)
58.
Solve the equation.
\({81x^{2}+198x+121}=0\)
59.
Solve the equation.
\({x\!\left(x^{2}+9x+8\right)} = 0\)
60.
Solve the equation.
\({\left(x+9\right)\!\left(x^{2}+7x+10\right)} = 0\)
61.
Solve the equation.
\({x\!\left(x^{2}-9\right)} = 0\)
62.
Solve the equation.
\({x\!\left(x^{2}-25\right)} = 0\)
63.
Solve the equation.
\({x^{3}-9x^{2}+14x} = 0\)
64.
Solve the equation.
\({x^{3}-6x^{2}-27x} = 0\)
Quadratic Equation Application Problems
For the following application problems, write and solve a quadratic equation, by factoring, to answer the questions.
65.
Two numbers’ sum is \(-3\text{,}\) and their product is \(-70\text{.}\) Find these two numbers.
These two numbers are .
66.
Two numbers’ sum is \(3\text{,}\) and their product is \(-54\text{.}\) Find these two numbers.
These two numbers are .
67.
A bomb exploded and the path of the debris from the explosion can be modeled by the equation \(h=96t-16t^2\text{,}\) where \(h\) represents the height, in feet, of the debris above the ground \(t\) seconds after the explosion. After how many seconds will the debris hit the ground?
How many seconds will it take for the debris to hit the ground?
seconds
68.
A bomb exploded and the path of the debris from the explosion can be modeled by the equation \(h=80t-16t^2\text{,}\) where \(h\) represents the height, in feet, of the debris above the ground \(t\) seconds after the explosion. After how many seconds will the debris hit the ground?
The debris will hit the ground after how many seconds?
seconds
69.
A pennant is shaped like a right triangle, with a hypothenuse that is \(10\) inches long. The length of one side of the pennant is \(2\) inches longer than the length of the other leg. Find the lengths of the two legs.
How long is the longer leg?
How long is the shorter leg?
in.; in.
70.
A reflecting pool is shaped like a right triangle, with one leg along the wall of a building. The hypotenuse is \(9\) feet longer than the side along the building. The third side is \(7\) feet longer than the side along the building. Find the lengths of all three sides.
ft.; ft.; ft.
71.
A rectangle’s base is \({5\ {\rm in}}\) shorter than four times its height. The rectangle’s area is \({21\ {\rm in^{2}}}\text{.}\) Find this rectangle’s dimensions.
The rectangle’s height is .
The rectangle’s base is .
72.
A rectangle’s base is \({4\ {\rm in}}\) shorter than three times its height. The rectangle’s area is \({32\ {\rm in^{2}}}\text{.}\) Find this rectangle’s dimensions.
The rectangle’s height is .
The rectangle’s base is .
73.
A rectangle’s base is \({9\ {\rm cm}}\) longer than its height. The rectangle’s area is \({136\ {\rm cm^{2}}}\text{.}\) Find this rectangle’s dimensions.
The rectangle’s height is .
The rectangle’s base is .
74.
A rectangle’s base is \({7\ {\rm cm}}\) longer than its height. The rectangle’s area is \({120\ {\rm cm^{2}}}\text{.}\) Find this rectangle’s dimensions.
The rectangle’s height is .
The rectangle’s base is .
75.
There is a rectangular lot in the garden, with \({9\ {\rm ft}}\) in length and \({5\ {\rm ft}}\) in width. You plan to expand the lot by an equal length around its four sides, and make the area of the expanded rectangle \({77\ {\rm ft^{2}}}\text{.}\) How long should you expand the original lot in four directions?
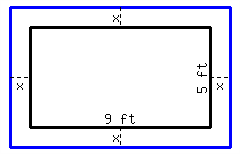
You should expand the original lot by in four directions.
76.
There is a rectangular lot in the garden, with \({9\ {\rm ft}}\) in length and \({5\ {\rm ft}}\) in width. You plan to expand the lot by an equal length around its four sides, and make the area of the expanded rectangle \({117\ {\rm ft^{2}}}\text{.}\) How long should you expand the original lot in four directions?
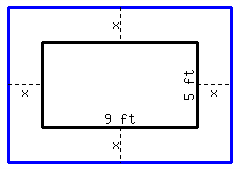
You should expand the original lot by in four directions.
Graphing Quadratic Equations
Graph each curve by algebraically determining its intercepts, vertex, and any other points necessary.
77.
\(y=-x^2-x+20\)
78.
\(y=-x^2+4x+21\)
79.
\(y=x^2+6x\)
80.
\(y=x^2-8x\)
81.
\(y=x^2-8x+16\)
82.
\(y=x^2+6x+9\)
83.
\(y=x^2-4\)
84.
\(y=x^2-9\)
85.
\(y=2x^2-4x-30\)
86.
\(y=3x^2+21x+36\)
Challenge
87.
Give an example of a cubic equation that has three solutions: one solution is \(x = 1\text{,}\) the second solution is \(x= -5\text{,}\) and the third solution is \(x = \frac{2}{3} \text{.}\)
88.
Solve for \(x\) in the equation \(8x^{28}-2x^{26} = 0 \text{.}\)
Some of Subsection 7.7.3 is adapted from Quadratic Equations 1 by Wendy Lightheart, OpenStax CNX, which is licensed under CC BY 4.0 2
