ORCCA More on Quadratic Functions Chapter Review

Section 11.5 More on Quadratic Functions Chapter Review

Subsection 11.5.1 Graphs and Vertex Form

In Section 11.1 we covered the vertex form of a quadratic function, how it can be used to identify the vertex, and how the vertex can be used to find the domain and range of a quadratic function. We also covered the factored form of a quadratic function and how it can help us identify horizontal intercepts.

Example 11.5.1. The Vertex Form of a Parabola.

Recall that the vertex form of a quadratic function tells us the location of the vertex of a parabola.

State the vertex of the quadratic function \(r(x)=-8(x+1)^2+7\) and its domain and range.
State the vertex of the quadratic function \(u(x)=5(x-7)^2-3\) and its domain and range.
Write the formula for a parabola with vertex \((-5,3)\) and \(a=2\text{.}\)
Write the formula for a parabola with vertex \((1,-17)\) and \(a=-4\text{.}\)

Explanation

The vertex of the quadratic function \(r(x)=-8(x+\highlight{1})^2+\lighthigh{7}\) is \((\highlight{-1},\lighthigh{7})\text{.}\) The domain of \(r\) is \((-\infty,\infty)\) and since the graph of \(r\) will be opening downward, the range of \(r\) is \((-\infty,7]\text{.}\)
The vertex of the quadratic function \(u(x)=5(x-\highlight{7})^2\lighthigh{-3}\) is \((\highlight{7},\lighthigh{-3})\text{.}\) The domain of \(u\) is \((-\infty,\infty)\) and since the graph of \(u\) will be opening upward, the range of \(r\) is \([-3,\infty)\text{.}\)
The formula for a parabola with vertex \((\highlight{-5},\lighthigh{3})\) and \(a=2\) is \(y=2(x+\highlight{5})^2+\lighthigh{3}\text{.}\)
The formula for a parabola with vertex \((\highlight{1},\lighthigh{-17})\) and \(a=-4\) is \(y=4(x-\highlight{1})^2\lighthigh{-17}\text{.}\)

Example 11.5.2. The Factored Form of a Parabola.

Recall that the factored form of a quadratic function tells us the horizontal intercepts very quickly.

\(n(x)=13(x-1)(x+6)\text{.}\)
\(p(x)=-6(x-\frac{2}{3})(x+\frac{1}{2})\text{.}\)

Explanation

The horizontal intercepts of \(n\) are \((1,0)\) and \((-6,0)\text{.}\)
The horizontal intercepts of \(p\) are \((\frac{2}{3},0)\) and \((-\frac{1}{2},0)\text{.}\)

Subsection 11.5.2 Completing the Square

In Section 11.2 we covered how to complete the square to both solve quadratic equations in one variable and to put quadratic functions into vertex form.

Example 11.5.3. Solving Quadratic Equations by Completing the Square.

Solve the equations by completing the square.

\(\displaystyle k^2-18k+1=0\)
\(\displaystyle 4p^2-3p=2\)

Explanation

To complete the square in the equation \(k^2-18k+1=0\text{,}\) we first we will first move the constant term to the right side of the equation. Then we will use Fact 11.2.1 to find \(\left(\frac{b}{2}\right)^2\) to add to both sides.

\begin{align*} k^2-18k+1\amp=0\\ k^2-18k\amp=-1 \end{align*}

In our case, \(b=-18\text{,}\) so \(\left(\frac{b}{2}\right)^2=\left(\frac{-18}{2}\right)^2=81\)

\begin{align*} k^2-18k\addright{81}\amp=-1\addright{81}\\ (k-9)^2\amp=80 \end{align*}

\begin{align*} k-9\amp=-\sqrt{80}\amp\text{ or }\amp\amp k-9\amp=\sqrt{80}\\ k-9\amp=-4\sqrt{5}\amp\text{ or }\amp\amp k-9\amp=4\sqrt{5}\\ k\amp=9-4\sqrt{5}\amp\text{ or }\amp\amp k\amp=9+4\sqrt{5} \end{align*}

The solution set is \(\{9+4\sqrt{5},9-4\sqrt{5}\}\text{.}\)
To complete the square in the equation \(4p^2-3p=2\text{,}\) we first divide both sides by \(4\) since the leading coefficient is 4.

\begin{align*} \divideunder{4p^2}{4}-\divideunder{3p}{4}\amp=\divideunder{2}{4}\\ p^2-\frac{3}{4}p\amp=\frac{1}{2}\\ p^2-\frac{3}{4}p\amp=\frac{1}{2} \end{align*}

Next, we will complete the square. Since \(b=-\frac{3}{4}\text{,}\) first,

\begin{equation} \frac{b}{2}=\frac{-\frac{3}{4}}{2}=-\frac{3}{8}\label{DsJ}\tag{11.5.1} \end{equation}

and next, squaring that, we have

\begin{equation} \left(-\frac{3}{8}\right)^2=\frac{9}{64}\text{.}\label{jzS}\tag{11.5.2} \end{equation}

So we will add \(\frac{9}{64}\) from Equation (11.5.2) to both sides of the equation:

\begin{align*} p^2-\frac{3}{4}p\addright{\frac{9}{64}}\amp=\frac{1}{2}\addright{\frac{9}{64}}\\ p^2-\frac{3}{4}p+\frac{9}{64}\amp=\frac{32}{64}+\frac{9}{64}\\ p^2-\frac{3}{4}p+\frac{9}{64}\amp=\frac{41}{64} \end{align*}

Here, remember that we always factor with the number found in the first step of completing the square, Equation (11.5.1).

\begin{align*} \left(p-\frac{3}{8}\right)^2\amp=\frac{41}{64} \end{align*}

\begin{align*} p-\frac{3}{8}\amp=-\frac{\sqrt{41}}{8}\amp\text{ or }\amp\amp p-\frac{3}{8}\amp=\frac{\sqrt{41}}{8}\\ p\amp=\frac{3}{8}-\frac{\sqrt{41}}{8}\amp\text{ or }\amp\amp p\amp=\frac{3}{8}+\frac{\sqrt{41}}{8}\\ p\amp=\frac{3-\sqrt{41}}{8}\amp\text{ or }\amp\amp p\amp=\frac{3+\sqrt{41}}{8} \end{align*}

The solution set is \(\left\{\frac{3-\sqrt{41}}{8}, \frac{3+\sqrt{41}}{8}\right\}\text{.}\)

Example 11.5.4. Putting Quadratic Functions in Vertex Form.

Write a formula in vertex form for the function \(T\) defined by \(T(x)=4x^2+20x+24\text{.}\)

Explanation

Before we can complete the square, we will factor the \(\highlight{4}\) out of the first two terms. Don't be tempted to factor the \(4\) out of the constant term.

\begin{align*} T(x)\amp=\highlight{4}\left(x^2+5x\right)+24 \end{align*}

Now we will complete the square inside the parentheses by adding and subtracting \(\left(\frac{5}{2}\right)^2=\frac{25}{4}\text{.}\)

\begin{align*} T(x)\amp=4\left(x^2+5x\addright{\frac{25}{4}}\subtractright{\frac{25}{4}}\right)+24 \end{align*}

Notice that the constant that we subtracted is inside the parentheses, but it will not be part of our perfect square trinomial. In order to bring it outside, we need to multiply it by \(4\text{.}\) We are distributing the \(4\) to that term so we can combine it with the outside term.

\begin{align*} T(x)\amp=4\left(\highlight{\left(\unhighlight{x^2+5x+\frac{25}{4}}\right)}-\highlight{\frac{25}{4}}\right)+24\\ \amp=4\highlight{\left(\unhighlight{x^2+5x+\frac{25}{4}}\right)}-\multiplyleft{4}\frac{25}{4}+24\\ \amp=4\left(x+\frac{5}{2}\right)^2-25+24\\ \amp=4\left(x+\frac{5}{2}\right)^2-1 \end{align*}

Note that The vertex is \(\left(-\frac{5}{2},-1\right)\text{.}\)

Example 11.5.5. Graphing Quadratic Functions by Hand.

Graph the function \(H\) defined by \(H(x)=-x^2-8x-15\) by determining its key features algebraically.

Explanation

To start, we'll note that this function opens downward because the leading coefficient, \(-1\text{,}\) is negative.

Now we will complete the square to find the vertex. We will factor the \(-1\) out of the first two terms, and then add and subtract \(\left(\frac{8}{2}\right)^2=4^2=\highlight{16}\) on the right side.

\begin{align*} H(x)\amp=-\left[x^2+8x\right]-15\\ \amp=-\left[x^2+8x\addright{16}\subtractright{16}\right]-15\\ \amp=-\left[\highlight{\left(\unhighlight{x^2+8x+16}\right)}-16\right]-15\\ \amp=-\highlight{\left(\unhighlight{x^2+8x+16}\right)}-\left(-1\cdot16\right)-15\\ \amp=-\left(x+4\right)^2+16-15\\ \amp=-\left(x+4\right)^2+1 \end{align*}

The vertex is \((-4,1)\) so the axis of symmetry is the line \(x=-4\text{.}\)

To find the \(y\)-intercept, we'll replace \(x\) with \(0\) or read the value of \(c\) from the function in standard form:

\begin{align*} H(\substitute{0})\amp=-(\substitute{0})^2-8(\substitute{0})-15\\ \amp=-15 \end{align*}

The \(y\)-intercept is \((0,-15)\) and we will find its symmetric point on the graph, which is \((-8,-15)\text{.}\)

Next, we'll find the horizontal intercepts. We see this function factors so we will write the factored form to get the horizontal intercepts.

\begin{align*} H(x)\amp=-x^2-8x-15\\ \amp=-\left(x^2+8x+15\right)\\ \amp=-(x+3)(x+5) \end{align*}

The \(x\)-intercepts are \((-3,0)\) and \((-5,0)\text{.}\)

Now we will plot all of the key points and draw the parabola.

a graph of the parabola y=-x^2-8x-15 opens downward and the key features are labeled; the vertex is (-4,1);the axis of symmetry is drawn at x=-4;the y-intercept is (0,-15) and its symmetric point is (-8,-15);the x-intercepts are (-3,0) and (-5,0). — Figure 11.5.6. The graph of \(y=-x^2-8x-15\text{.}\)

Subsection 11.5.3 More on Complex Solutions to Quadratic Equations

In Section 11.3 we covered the definition of a complex number, and discussed both quadratic applications and equations where complex numbers appear as solutions.

Example 11.5.7. Applications with Real or Complex Solutions.

One day, Samar was bouncing a ball inside the house. The trajectory of his bounce followed the quadratic function \(H(t)=-16t^2+24t\text{,}\) where \(H(t)\) describes the height of the ball, in feet, at time \(t\) seconds after it bounced off the ground. If the ceilings in Samar's house were \(10\) feet tall, find out if the ball will hit the ceiling.

Explanation

To find out if the ball will hit the ceiling, we need to set the formula for the function equal to \(\substitute{10}\) and solve.

\begin{align*} \substitute{H(t)}\amp=-16t^2+24t\\ \substitute{10}\amp=-16t^2+24t\\ 0\amp=-16t^2+24t-10\\ \end{align*}

This is a quadratic equation where verything is divisible by \(2\text{.}\) We will divide every term by \(2\) which can simplify the process.

\begin{align*} \divideunder{0}{2}\amp=\divideunder{-16t^2}{2}+\divideunder{24t}{2}-\divideunder{10}{2}\\ 0\amp=-8t^2+12t-5\\ \end{align*}

Since the equation doesn't seem to factor easily, we will use the quadratic formula to solve it. Note that \(\substitute{a=-8}\text{,}\) \(\substitute{b=12}\text{,}\) and \(\substitute{c=-5}\text{.}\)

\begin{align*} t\amp=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ t\amp=\frac{-(\substitute{12})\pm\sqrt{(\substitute{12})^2-4(\substitute{-8})(\substitute{-5})}}{2(\substitute{-8})}\\ t\amp=\frac{-12\pm\sqrt{-16}}{-16}\\ \end{align*}

Note that the discriminant is negative, which means that the equation has no real solutions. Just for practice, we will finish the simplification process, but we are ready to make our conclusion here.

\begin{align*} t\amp=\frac{-12\pm\sqrt{\highlight{16}\cdot\lighthigh{-1}}}{-16}\\ t\amp=\frac{-12\pm\highlight{4}\lighthigh{i}}{-16}\\ t\amp=\frac{-12}{-16}\pm\frac{\highlight{4}\lighthigh{i}}{-16}\\ t\amp=\frac{3}{4}\mp\frac{\lighthigh{i}}{4} \end{align*}

Since the solutions to the equation are complex numbers, the reality of the situation must be that the ball never does hit the ceiling. Samar's ceiling lights are safe for now.

Example 11.5.8. Solving Equations with Complex Solutions.

Solve for \(x\) in \(3x^2-12x+36=0\text{.}\)

Explanation

We will use the completing-the-square method. To do so, we first need to divide both sides by the leading coefficient, \(3\text{.}\)

\begin{align*} 3x^2-12x+36\amp=0\\ 3x^2-12x\amp=-36\\ \divideunder{3x^2}{3}-\divideunder{12x}{3}\amp=\divideunder{-36}{3}\\ x^2-4x\amp=-12\\ \end{align*}

Now we can add \(\left(\frac{b}{2}\right)^2=(-2)^2=4\) to both sides to complete the square.

\begin{align*} x^2-4x\addright{4}\amp=-12\addright{4}\\ (x-2)^2\amp=-8 \end{align*}

\begin{align*} x-2\amp=-\sqrt{-8}\amp\amp\text{ or }\amp x-2\amp=\sqrt{-8}\\ x-2\amp=-\sqrt{\highlight{4}\cdot\lighthigh{-1}\cdot2}\amp\amp\text{ or }\amp x-2\amp=\sqrt{\highlight{4}\cdot\lighthigh{-1}\cdot2}\\ x-2\amp=-\highlight{2}\lighthigh{i}\sqrt{2}\amp\amp\text{ or }\amp x-2\amp=\highlight{2}\lighthigh{i}\sqrt{2}\\ x\amp=2-\highlight{2}\lighthigh{i}\sqrt{2}\amp\amp\text{ or }\amp x\amp=2+\highlight{2}\lighthigh{i}\sqrt{2} \end{align*}

The solution set is \(\{2-\highlight{2}\lighthigh{i}\sqrt{2}, 2+\highlight{2}\lighthigh{i}\sqrt{2}\}\text{.}\)

Subsection 11.5.4 Complex Number Operations

In Section 11.4 we covered the essential algebra of complex numbers.

Example 11.5.9. Adding and Subtracting Complex Numbers.

Simplify the expression \((5-3i)-(1-7i)\text{.}\)

Explanation

\begin{align*} (5-3i)-(1-7i)\amp=5-3\highlight{i}-1+7\highlight{i}\\ \amp=4+4\highlight{i} \end{align*}

Example 11.5.10. Multiplying Complex Numbers.

Multiply \((3+2i)(5-6i)\text{.}\)

Explanation

We will use the FOIL method to multiply the two binomials.

\begin{align*} (1+5i)(2-7i)\amp=15-18\highlight{i}+10\highlight{i}-12\highlight{i}^2\\ \amp=15-8\highlight{i}-12(-1)\\ \amp=15-8\highlight{i}+12\\ \amp=27-8\highlight{i} \end{align*}

Example 11.5.11. Dividing Complex Numbers.

Simplify the expression \(\frac{3+5i}{5-6i}\text{.}\)

Explanation

To divide complex numbers, we rationalize the denominator using the conjugate \(2+4i\text{:}\)

\begin{align*} \frac{3+5i}{5-6i}\amp=\frac{(3+5i)}{(5-6i)}\multiplyright{\frac{(5+6i)}{(5+6i)}}\\ \amp=\frac{15+18\highlight{i}+25\highlight{i}+30\highlight{i}^2}{25+30\highlight{i}-30\highlight{i}-36\highlight{i}^2}\\ \amp=\frac{15+43\highlight{i}+30(-1)}{25-36(-1)}\\ \amp=\frac{15+43\highlight{i}-30}{25+36}\\ \amp=\frac{-15+43\highlight{i}}{61}\\ \amp=-\frac{15}{61}+\frac{43\highlight{i}}{61} \end{align*}

Exercises 11.5.5 Exercises

Graphs and Vertex Form

Evaluate the function for several values of \(x\) to make a table.

1.

Make a table of values for the function \(K\) defined by \(K(x)={x^{2}-3x-2}\text{.}\)

\(x\)	\(K(x)\)

2.

Make a table of values for the function \(f\) defined by \(f(x)={x^{2}+x-2}\text{.}\)

\(x\)	\(f(x)\)

3.

Make a table of values for the function \(g\) defined by \(g(x)={-x^{2}+2x+1}\text{.}\)

\(x\)	\(g(x)\)

4.

Make a table of values for the function \(g\) defined by \(g(x)={-x^{2}-4x+1}\text{.}\)

\(x\)	\(g(x)\)

5.

Make a table of values for the function \(h\) defined by \(h(x)={3x^{2}-4x-6}\text{.}\)

\(x\)	\(h(x)\)

6.

Make a table of values for the function \(F\) defined by \(F(x)={-2x^{2}+8x-6}\text{.}\)

\(x\)	\(F(x)\)

7.

Let \(G(x)={x^{2}-3x+3}\text{.}\) Find the following.

Any decimal answers should be correct to four significant digits.

The vertex is .
The \(y\)-intercept is .
The \(x\)-intercept(s) is/are .

If there are no \(x\)-intercepts, enter NONE. If there are more than one, use commas to separate the points.
The domain of \(G\) is .

Use interval notation.
The range of \(G\) is .

Use interval notation.
Calculate \(G(4)\text{.}\) .
Solve \(G(x)=6\text{.}\)
Solve \(G(x)\leq6\text{.}\)

Use interval notation. If you need to write a union of intervals, use U for the union symbol.

8.

Let \(G(x)={-2x^{2}-3x-1}\text{.}\) Find the following.

Any decimal answers should be correct to four significant digits.

The vertex is .
The \(y\)-intercept is .
The \(x\)-intercept(s) is/are .

If there are no \(x\)-intercepts, enter NONE. If there are more than one, use commas to separate the points.
The domain of \(G\) is .

Use interval notation.
The range of \(G\) is .

Use interval notation.
Calculate \(G(-2)\text{.}\) .
Solve \(G(x)=-4\text{.}\)
Solve \(G(x)\geq-4\text{.}\)

Use interval notation. If you need to write a union of intervals, use U for the union symbol.

9.

An object was launched from the top of a hill with an upward vertical velocity of \(180\) feet per second. The height of the object can be modeled by the function \(h(t)={-16t^{2}+180t+150}\text{,}\) where \(t\) represents the number of seconds after the launch. Assume the object landed on the ground at sea level. Find the answer algebraically.

seconds after its launch, the object reached its maximum height of feet.

10.

An object was launched from the top of a hill with an upward vertical velocity of \(190\) feet per second. The height of the object can be modeled by the function \(h(t)={-16t^{2}+190t+300}\text{,}\) where \(t\) represents the number of seconds after the launch. Assume the object landed on the ground at sea level. Find the answer algebraically.

seconds after its launch, the object fell to the ground at sea level.

11.

Find the vertex of the graph of \(y=-10\!\left(x-3\right)^{2}-1\text{.}\)

12.

Find the vertex of the graph of \(y=-7\!\left(x+4\right)^{2}+7\text{.}\)

13.

Write the vertex form for the quadratic function \(f\text{,}\) whose vertex is \((8,-4)\) and has leading coefficient \(a=-4\text{.}\)

14.

Write the vertex form for the quadratic function \(f\text{,}\) whose vertex is \((2,3)\) and has leading coefficient \(a=-2\text{.}\)

15.

A graph of a function \(f\) is given. Use the graph to write a formula for \(f\) in vertex form. You will need to identify the vertex and also one more point on the graph to find the leading coefficient \(a\text{.}\)

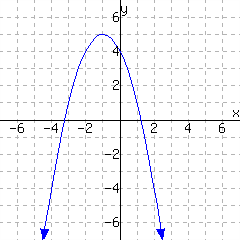
\(\displaystyle{ f(x) =}\)

16.

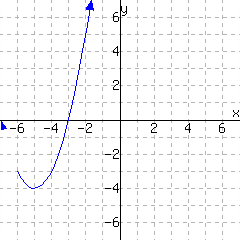
\(\displaystyle{ f(x) =}\)

17.

Let \(G\) be defined by \(G(x)={\left(x-1\right)^{2}+8}\text{.}\)

What is the domain of \(G\text{?}\)
What is the range of \(G\text{?}\)

18.

Let \(H\) be defined by \(H(x)={\left(x+6\right)^{2}-3}\text{.}\)

What is the domain of \(H\text{?}\)
What is the range of \(H\text{?}\)

19.

The quadratic expression \({\left(x-4\right)^{2}-64}\) is written in vertex form.

Write the expression in standard form.
Write the expression in factored form.

20.

The quadratic expression \({\left(x-1\right)^{2}-4}\) is written in vertex form.

Write the expression in standard form.
Write the expression in factored form.

21.

The formula for a quadratic function \(G\) is \(G(x)={\left(x+7\right)\!\left(x+6\right)}\text{.}\)

The \(y\)-intercept is .
The \(x\)-intercept(s) is/are .

If there are no \(x\)-intercepts, enter NONE. If there are more than one, use commas to separate the points.

22.

The formula for a quadratic function \(f\) is \(f(x)={\left(x+4\right)\!\left(x-6\right)}\text{.}\)

The \(y\)-intercept is .
The \(x\)-intercept(s) is/are .

If there are no \(x\)-intercepts, enter NONE. If there are more than one, use commas to separate the points.

Completing the Square

23.

Solve \({y^{2}-2y}={24}\) by completing the square.

24.

Solve \({y^{2}+4y}={45}\) by completing the square.

25.

Solve \({r^{2}-r-20}={0}\) by completing the square.

26.

Solve \({r^{2}-3r-4}={0}\) by completing the square.

27.

Solve \({3t^{2}-4t+1}={0}\) by completing the square.

28.

Solve \({3t^{2}-16t+21}={0}\) by completing the square.

29.

Complete the square to convert the quadratic function from standard form to vertex form, and use the result to find the function’s domain and range.

\(f(x) = {-5x^{2}-100x-502}\)

The domain of \(f\) is

The range of \(f\) is

30.

Complete the square to convert the quadratic function from standard form to vertex form, and use the result to find the function’s domain and range.

\(f(x) = {-3x^{2}-42x-157}\)

The domain of \(f\) is

The range of \(f\) is

31.

Graph \(f(x)=x^2-7x+12\) by algebraically determining its key features. Then state the domain and range of the function.

32.

Graph \(f(x)=-x^2+4x+21\) by algebraically determining its key features. Then state the domain and range of the function.

33.

Graph \(f(x)=x^2-8x+16\) by algebraically determining its key features. Then state the domain and range of the function.

34.

Graph \(f(x)=x^2+6x+9\) by algebraically determining its key features. Then state the domain and range of the function.

35.

Graph \(f(x)=x^2+4x+7\) by algebraically determining its key features. Then state the domain and range of the function.

36.

Graph \(f(x)=x^2-2x+6\) by algebraically determining its key features. Then state the domain and range of the function.

37.

Graph \(f(x)=2x^2-4x-30\) by algebraically determining its key features. Then state the domain and range of the function.

38.

Graph \(f(x)=3x^2+21x+36\) by algebraically determining its key features. Then state the domain and range of the function.

39.

Find the minimum value of the function

\begin{equation*} f(x)=3x^{2}+4x+6 \end{equation*}

40.

Find the minimum value of the function

\begin{equation*} f(x)=4x^{2}-3x-7 \end{equation*}

41.

Solve the quadratic equation. Solutions could be complex numbers.

\(6(y - 7)^2+4 = -596\)

42.

Solve the quadratic equation. Solutions could be complex numbers.

\(-4(r - 10)^2+3 = 199\)

43.

Solve the quadratic equation. Solutions could be complex numbers.

\({r^{2}-2r+4} =0\)

44.

Solve the quadratic equation. Solutions could be complex numbers.

\({t^{2}+8t+23} =0\)

45.

A remote control aircraft will perform a stunt by flying toward the ground and then up. Its height, in feet, can be modeled by the equation \(h={0.8t^{2}-16t+81}\text{,}\) where \(t\) is in seconds. The plane

will
will not

hit the ground during this stunt.

46.

A remote control aircraft will perform a stunt by flying toward the ground and then up. Its height, in feet, can be modeled by the equation \(h={1.3t^{2}-7.8t+8.7}\text{,}\) where \(t\) is in seconds. The plane

will
will not

hit the ground during this stunt.

Complex Number Operations

47.

Write the complex number in standard form.

\begin{equation*} (-7+9i)-(-8+7i) \end{equation*}

48.

Write the complex number in standard form.

\begin{equation*} (-5+i)-(2i) \end{equation*}

49.

Write the complex number in standard form.

\begin{equation*} (-3-6i)(9-4i) \end{equation*}

50.

Write the complex number in standard form.

\begin{equation*} (8i)(-3-10i) \end{equation*}

51.

Rewrite the following expression into the form of a+b\(i\text{:}\)

\(\displaystyle{ \frac{{2+5i}}{{4+i}} = }\)

52.

Rewrite the following expression into the form of a+b\(i\text{:}\)

\(\displaystyle{ \frac{{3-6i}}{{-5-i}} = }\)