ORCCA Linear Equations and Inequalities Chapter Review

Section 3.7 Linear Equations and Inequalities Chapter Review

Subsection 3.7.1 Solving Multistep Linear Equations

In Section 3.1 we covered the steps to solve a linear equation and the differences among simplifying expressions, evaluating expressions and solving equations.

Example 3.7.1.

Solve for $a$ in $4-(3-a)=-2-2(2a+1)\text{.}$

Explanation

To solve this equation, we will simplify each side of the equation, manipulate it so that all variable terms are on one side and all constant terms are on the other, and then solve for $a\text{:}$

\begin{align*} 4-(3-a)\amp=-2-2(2a+1)\\ 4-3+a\amp=-2-4a-2\\ 1+a\amp=-4-4a\\ 1+a\addright{4a}\amp=-4-4a\addright{4a}\\ 1+5a\amp=-4\\ 1+5a\subtractright{1}\amp=-4\subtractright{1}\\ 5a\amp=-5\\ \divideunder{5a}{5}\amp=\divideunder{-5}{5}\\ a\amp=-1 \end{align*}

Checking the solution $-1$ in the original equation, we get:

\begin{align*} 4-(3-a)\amp=-2-2(2a+1)\\ 4-(3-(\substitute{-1}))\amp\stackrel{?}{=}-2-2(2(\substitute{-1})+1)\\ 4-(4)\amp\stackrel{?}{=}-2-2(-1)\\ 0\amp\stackrel{\checkmark}{=}0 \end{align*}

Therefore, the solution to the equation is $-1$ and the solution set is $\{-1\}\text{.}$

Differentiating among Simplifying Expressions, Evaluating Expressions, and Solving Equations.

Let's summarize the differences among simplifying expressions, evaluating expressions, and solving equations:

An expression like $10-3(x+2)$ can be simplified to $-3x+4$ (as in Example 3.1.14), but we cannot solve for $x$ in an expression.
As $x$ takes different values, an expression has different values. In Example 3.1.15, when $x=2\text{,}$ $10-3(x+2)=-2\text{;}$ but when $x=3\text{,}$ $10-3(x+2)=-5\text{.}$
An equation connects two expressions with an equals sign. In Example 3.1.16, $10-3(x+2)=x-16$ has the expression $10-3(x+2)$ on the left side of equals sign and the expression $x-16$ on the right side.
When we solve the equation $10-3(x+2)=x-16\text{,}$ we are looking for a number which makes those two expressions have the same value. In Example 3.1.16, we found the solution to be $x=5\text{,}$ which makes both $10-3(x+2)=-11$ and $x-16=-11\text{,}$ as shown in the checking part.

Subsection 3.7.2 Solving Multistep Linear Inequalities

In Section 3.2 we covered how solving inequalities is very much like how we solve equations, except that if we multiply or divide by a negative we switch the inequality sign.

Example 3.7.2.

Solve for $x$ in $-2-2(2x+1)\gt4-(3-x)\text{.}$ Write the solution set in both set-builder notation and interval notation.

Explanation

\begin{align*} -2-2(2x+1)\amp\gt4-(3-x)\\ -2-4x-2\amp\gt4-3+x\\ -4x-4\amp\gt x+1\\ -4x-4\subtractright{x}\amp\gt x+1\subtractright{x}\\ -5x-4\amp\gt1\\ -5x-4\addright{4}\amp\gt1\addright{4}\\ -5x\amp\gt5\\ \divideunder{-5x}{-5}\amp\lt\divideunder{5}{-5}\\ x\amp\lt-1 \end{align*}

Note that when we divided both sides of the inequality by $-5\text{,}$ we had to switch the direction of the inequality symbol.

The solution set in set-builder notation is $\{x\mid x\lt-1\}\text{.}$ The solution set in interval notation is $(-\infty,-1)\text{.}$

Subsection 3.7.3 Linear Equations and Inequalities with Fractions

In Section 3.3 we covered how to eliminate denominators in an equation with the LCD to help solve the equation.

Example 3.7.3.

Solve for $x$ in $\frac{1}{4}x+\frac{2}{3}=\frac{1}{6}\text{.}$

Explanation

We'll solve by multiplying each side of the equation by $12\text{:}$

\begin{align*} \frac{1}{4}x+\frac{2}{3}\amp=\frac{1}{6}\\ \multiplyleft{12}\left(\frac{1}{4}x+\frac{2}{3}\right)\amp=\multiplyleft{12}\frac{1}{6}\\ 12\cdot\left(\frac{1}{4}x\right)+12\cdot\left(\frac{2}{3}\right)\amp=12\cdot\frac{1}{6}\\ 3x+8\amp=2\\ 3x\amp=-6\\ \divideunder{3x}{3}\amp=\divideunder{-6}{3}\\ x\amp=-2 \end{align*}

Checking the solution:

\begin{align*} \frac{1}{4}x+\frac{2}{3}\amp=\frac{1}{6}\\ \frac{1}{4}(\substitute{-2})+\frac{2}{3}\amp\stackrel{?}{=}\frac{1}{6}\\ -\frac{2}{4}+\frac{2}{3}\amp\stackrel{?}{=}\frac{1}{6}\\ -\frac{6}{12}+\frac{8}{12}\amp\stackrel{?}{=}\frac{1}{6}\\ \frac{2}{12}\amp\stackrel{?}{=}\frac{1}{6}\\ \frac{1}{6}\amp\stackrel{\checkmark}{=}\frac{1}{6} \end{align*}

The solution is therefore $-2\text{.}$ We write the solution set s $\{-2\}\text{.}$

Subsection 3.7.4 Isolating a Linear Variable

In Section 3.4 we covered how to solve an equation when there are multiple variables in the equation.

Example 3.7.4.

Solve for $x$ in $y=mx+b\text{.}$

Explanation

\begin{align*} y\amp=mx+b\\ y\subtractright{b}\amp=mx+b\subtractright{b}\\ y-b\amp=mx\\ \divideunder{y-b}{m}\amp=\divideunder{mx}{m}\\ \frac{y-b}{m}\amp=x \end{align*}

Subsection 3.7.5 Ratios and Proportions

In Section 3.5 we covered the definitions of a ratio and a proportion and how to solve a proportion. We learned about cross multiplication, did problems about similar triangles, and used proportions to solve word problems.

Example 3.7.5.

Solve $\frac{6-x}{5}=\frac{x}{4}$ for $x\text{.}$

Explanation

To solve this proportion, begin by multiplying both sides by both denominators.

\begin{align*} \frac{6-x}{5}\amp=\frac{x}{4}\\ \multiplyleft{5\cdot4}\frac{6-x}{5}\amp=\frac{x}{4}\multiplyright{5\cdot4}\\ \cancelhighlight{5}\cdot4\cdot\frac{6-x}{\cancelhighlight{5}}\amp=\frac{x}{\cancelhighlight{4}}\cdot5\cdot\cancelhighlight{4}\\ 4\cdot(6-x)\amp=x\cdot5\\ 24-4x\amp=5x\\ 24-4x\addright{4x}\amp=5x\addright{4x}\\ 24\amp=9x\\ \divideunder{24}{9}\amp=\divideunder{9x}{9}\\ \frac{24}{9}\amp=x \end{align*}

So, the solution set is $\left\{\frac{24}{9}\right\}\text{.}$

Example 3.7.6.

Property taxes for a residential property are proportional to the assessed value of the property. Assume that a certain property in a given neighborhood is assessed at $\$234{,}100$ and its annual property taxes are $\$2{,}518.92\text{.}$ What are the annual property taxes for a house that is assessed at $\$287{,}500\text{?}$

Explanation

Let $T$ be the annual property taxes (in dollars) for a property assessed at $\$287{,}500\text{.}$ We can write and solve this proportion:

\begin{align*} \frac{\text{tax}}{\text{property value}}\amp=\frac{\text{tax}}{\text{property value}}\\ \frac{2518.92}{234100}\amp=\frac{T}{287500}\\ \multiplyleft{234100\cdot287500}\frac{2518.92}{234100}\amp=\frac{T}{287500}\multiplyright{234100\cdot287500}\\ 287500\cdot2518.92 \amp=T\cdot 234100\\ \frac{287500\cdot 2518.92}{234100} \amp=\frac{234100T}{234100}\\ T\amp\approx3093.50 \end{align*}

The property taxes for a property assessed at $\$287{,}500$ are $\$3{,}093.50\text{.}$

Example 3.7.7.

Figure 3.7.8. Similar Triangles

Since the two triangles are similar, we know that their side length should be proportional. To determine the unknown length, we can set up a proportion and solve for $x\text{:}$

\begin{align*} \frac{\text{bigger triangle's left side length in cm}}{\text{bigger triangle's bottom side length in cm}}\amp=\frac{\text{smaller triangle's left side length in cm}}{\text{smaller triangle's bottom side length in cm}}\\ \frac{x\,\text{cm}}{6\,\text{cm}}\amp=\frac{3\,\text{cm}}{4\,\text{cm}}\\ \frac{x}{6}\amp=\frac{3}{4}\\ \multiplyleft{12}\frac{x}{6}\amp=\multiplyleft{12}\frac{3}{4}\qquad\text{(12 is the least common denominator)}\\ 2x\amp=9\\ \divideunder{2x}{2}\amp=\divideunder{9}{2}\\ x\amp=\frac{9}{2}\ \text{or}\ 4.5 \end{align*}

The unknown side length is then 4.5 cm.

Subsection 3.7.6 Special Solution Sets

In Section 3.6 we covered linear equations that have no solutions and also linear equations that have infinitely many solutions. When solving linear inequalities, it's also possible that no solution exists or that all real numbers are solutions.

Example 3.7.9.

Solve for $x$ in the equation $3x=3x+4\text{.}$
Solve for $t$ in the inequality $4t+5\gt 4t+2\text{.}$

Explanation

To solve this equation, we need to move all terms containing $x$ to one side of the equals sign:

\begin{align*} 3x\amp=3x+4\\ 3x\subtractright{3x}\amp=3x+4\subtractright{3x}\\ 0\amp=4 \end{align*}

This equation has no solution. We write the solution set as $\emptyset\text{,}$ which is the symbol for the empty set.
To solve for $t\text{,}$ we will first subtract $4t$ from each side to get all terms containing $t$ on one side:

\begin{align*} 4t+5\amp\gt 4t+2\\ 4t+5\subtractright{4t}\amp\gt 4t+2\subtractright{4t}\\ 5\amp\gt 2 \end{align*}

All values of the variable $t$ make the inequality true. The solution set is all real numbers, which we can write as $\{t\mid t\text{ is a real number}\}$ in set notation, or $(-\infty,\infty)$ in interval notation.

Exercises 3.7.7 Exercises

1.

Solve $\displaystyle{ {4\!\left(y+8\right)+6}={70} }\text{.}$
Evaluate $\displaystyle{{4\!\left(y+8\right)+6}}$ when $y=8\text{.}$
Simplify $\displaystyle{{4\!\left(y+8\right)+6}}\text{.}$

2.

Solve $\displaystyle{ {3\!\left(y-3\right)+1}={16} }\text{.}$
Evaluate $\displaystyle{{3\!\left(y-3\right)+1}}$ when $y=8\text{.}$
Simplify $\displaystyle{{3\!\left(y-3\right)+1}}\text{.}$

3.

Solve the equation.

${7}={-2A-8-A}$

4.

Solve the equation.

${87}={-8C-3-C}$

5.

Solve the equation.

$\displaystyle{ {2+9\!\left(n-8\right)}={-36-\left(6-2n\right)} }$

6.

Solve the equation.

$\displaystyle{ {1+10\!\left(p-6\right)}={-34-\left(1-2p\right)} }$

7.

Solve the equation.

$\displaystyle{ -8-7x+2 = -x+11-6x }$

8.

Solve the equation.

$\displaystyle{ -6-9y+6 = -y+13-8y }$

9.

Solve the equation.

$\displaystyle{ {26}={\frac{t}{9}+\frac{t}{4}} }$

10.

Solve the equation.

$\displaystyle{ {30}={\frac{a}{7}+\frac{a}{8}} }$

11.

Solve the equation.

$\displaystyle{ {\frac{c-1}{2}}={\frac{c+1}{4}} }$

12.

Solve the equation.

$\displaystyle{ {\frac{A-5}{6}}={\frac{A+8}{8}} }$

13.

Solve this inequality: ${4-\left(y+8\right)} \lt {-13}$

14.

Solve this inequality: ${4-\left(y+7\right)} \lt {1}$

15.

Solve this inequality: ${-5x} \geq {20}$

16.

Solve this inequality: ${-2x} \geq {6}$

17.

Solve this inequality: ${1+7\!\left(x-7\right)} \lt {-48-\left(6-4x\right)}$

18.

Solve this inequality: ${2+10\!\left(x-10\right)} \lt {-156-\left(6-2x\right)}$

19.

Solve this inequality: ${2} \leq {x+8}$

20.

Solve this inequality: ${3} \leq {x+6}$

21.

Solve this linear equation for $x\text{.}$

\begin{equation*} Ax+By=C \end{equation*}

22.

Solve this linear equation for $y\text{.}$

\begin{equation*} Ax+By=C \end{equation*}

23.

Solve this linear equation for $m\text{.}$

\begin{equation*} A=c-\frac{7m}{y} \end{equation*}

24.

Solve this linear equation for $p\text{.}$

\begin{equation*} b=c-\frac{2p}{m} \end{equation*}

25.

Jay has ${\$70}$ in his piggy bank. He plans to purchase some Pokemon cards, which costs ${\$1.95}$ each. He plans to save ${\$56.35}$ to purchase another toy. At most how many Pokemon cards can he purchase?

Write an equation to solve this problem.

Jay can purchase at most Pokemon cards.

26.

Aaron has ${\$72}$ in his piggy bank. He plans to purchase some Pokemon cards, which costs ${\$1.35}$ each. He plans to save ${\$46.35}$ to purchase another toy. At most how many Pokemon cards can he purchase?

Write an equation to solve this problem.

Aaron can purchase at most Pokemon cards.

27.

Use a linear equation to solve the word problem.

Nathan has ${\$100.00}$ in his piggy bank, and he spends ${\$1.50}$ every day. Maygen has ${\$5.50}$ in her piggy bank, and she saves ${\$3.00}$ every day.

If they continue to spend and save money this way, how many days later would they have the same amount of money in their piggy banks?

days later, Nathan and Maygen will have the same amount of money in their piggy banks.

28.

Use a linear equation to solve the word problem.

Farshad has ${\$60.00}$ in his piggy bank, and he spends ${\$1.50}$ every day. Farshad has ${\$10.50}$ in his piggy bank, and he saves ${\$3.00}$ every day.

If they continue to spend and save money this way, how many days later would they have the same amount of money in their piggy banks?

days later, Farshad and Farshad will have the same amount of money in their piggy banks.

29.

A hockey team played a total of $130$ games last season. The number of games they won was $10$ more than four times of the number of games they lost.

Write and solve an equation to answer the following questions.

The team lost games. The team won games.

30.

A hockey team played a total of $173$ games last season. The number of games they won was $17$ more than five times of the number of games they lost.

Write and solve an equation to answer the following questions.

The team lost games. The team won games.

31.

A rectangle’s perimeter is ${168\ {\rm ft}}\text{.}$ Its length is ${3\ {\rm ft}}$ longer than two times its width. Use an equation to find the rectangle’s length and width.

Its width is .

Its length is .

32.

A rectangle’s perimeter is ${290\ {\rm ft}}\text{.}$ Its length is ${5\ {\rm ft}}$ longer than four times its width. Use an equation to find the rectangle’s length and width.

Its width is .

Its length is .

33.

James has saved ${\$42.00}$ in his piggy bank, and he decided to start spending them. He spends ${\$5.00}$ every $9$ days. After how many days will he have ${\$17.00}$ left in the piggy bank?

James will have ${\$17.00}$ left in his piggy bank after days.

34.

Wenwu has saved ${\$47.00}$ in his piggy bank, and he decided to start spending them. He spends ${\$5.00}$ every $7$ days. After how many days will he have ${\$27.00}$ left in the piggy bank?

Wenwu will have ${\$27.00}$ left in his piggy bank after days.

35.

The following two triangles are similar to each other. Find the length of the missing side.

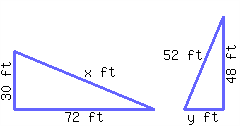
The length of the side labeled $x$ is and the length of the side labeled $y$ is .

36.

The following two triangles are similar to each other. Find the length of the missing side.

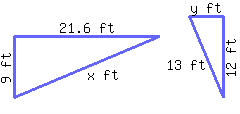
The length of the side labeled $x$ is and the length of the side labeled $y$ is .

37.

A restaurant used ${1025.7\ {\rm lb}}$ of vegetable oil in $39$ days. At this rate, ${1525.4\ {\rm lb}}$ of oil will last how many days?

The restaurant will use ${1525.4\ {\rm lb}}$ of vegetable oil in days.

38.

A restaurant used ${774.8\ {\rm lb}}$ of vegetable oil in $26$ days. At this rate, ${1549.6\ {\rm lb}}$ of oil will last how many days?

The restaurant will use ${1549.6\ {\rm lb}}$ of vegetable oil in days.

39.

Use a linear equation to solve the word problem.

Two truck rental companies have different rates. V-Haul has a base charge of ${\$65.00}\text{,}$ plus ${\$0.55}$ per mile. W-Haul has a base charge of ${\$45.80}\text{,}$ plus ${\$0.70}$ per mile. For how many miles would these two companies charge the same amount?

If a driver drives miles, those two companies would charge the same amount of money.

40.

A rectangle’s perimeter is ${100\ {\rm ft}}\text{.}$ Its length is ${1\ {\rm ft}}$ shorter than two times its width. Use an equation to find the rectangle’s length and width.

Its width is .

Its length is .

41.

A rectangle’s perimeter is ${286\ {\rm ft}}\text{.}$ Its length is ${3\ {\rm ft}}$ longer than four times its width. Use an equation to find the rectangle’s length and width.

Its width is .

Its length is .