ORCCA Applications of Systems of Linear Equations

Section 5.4 Applications of Systems of Linear Equations

Example 5.4.1 below is an example of how a system of linear equations can be used to solve an application problem. In this section, we will look at several types of application problems that can be solved using a system of linear equations, while giving you some strategies for solving these problems.

Subsection 5.4.1 A Strategy for Solving Applications of Systems of Linear Equations

Example 5.4.1.

Alicia has $\$1000$ to give to her two grandchildren for New Year's. She would like to give the older grandchild $\$120$ more than the younger grandchild, because that is the cost of the older grandchild's college textbooks this term. How much money should she give to each grandchild?

As always, we start solving a word problem by defining the variables, including their units. Let $A$ be the dollar amount she gives to her older grandchild, and $B$ be the dollar amount she gives to her younger grandchild. Since the total she has to give is $\$1000\text{,}$ we can say that $A+B=1000\text{.}$ Since she wants to give $\$120$ more to the older grandchild, we can say that the difference between the amounts is $\$120\text{,}$ or translated as a linear equation, $A-B=120\text{.}$ This gives us two linear equations, which together makes a system of linear equations:

\begin{align*} \left\{ \begin{aligned} A+B \amp = 1000 \\ A-B \amp = 120 \end{aligned} \right. \end{align*}

We can solve this system by either substitution as we learned in Section 5.2 or by elimination as we learned in Section 5.3. Notice that if we add together the left sides from the two equations, the variable $B$ will be eliminated quite easily:

\begin{align*} \begin{aligned}A+B\\{}+A-B\end{aligned}\amp=\begin{aligned}1000\\{}+120\end{aligned}\\ \end{align*}

So we have:

\begin{align*} 2A\amp=1120 \end{align*}

Thus, the elimination method is an easy method to use and it doesn't take much to finish solving for $A\text{:}$

\begin{align*} 2A\amp=1120\\ A\amp=560 \end{align*}

To finish solving this system of equations, we need the value of $B\text{.}$ For now, an easy way to find $B$ is to substitute in our value of $A$ into one of the original equations:

\begin{align*} A+B\amp=1000\\ \substitute{560}+B\amp=1000\\ B\amp=440 \end{align*}

To check our work, substitute $A=560$ and $B=440$ into the original equations:

\begin{align*} A+B\amp=1000\amp A-B\amp=120\\ \substitute{560}+\substitute{440}\amp\stackrel{?}{=}1000\amp \substitute{560}-\substitute{440}\amp\stackrel{?}{=}120\\ 1000\amp\stackrel{\checkmark}{=}1000\amp 120\amp\stackrel{\checkmark}{=}120 \end{align*}

This confirms that our solution is correct. In summary, Alicia should give $\$560$ to her older grandchild and $\$440$ to her younger grandchild.

Below is a general problem solving strategy for solving application problems, using systems of linear equations:

List 5.4.2. A Problem Solving Strategy for Applications of Systems of Linear Equations

Step 1: Read: Read the problem. Make sure all the words and ideas are understood. Draw a picture or diagram, if applicable.
Step 2: Identify: Identify what you are looking for.
Step 3: Name: Name what you are looking for by choosing variables to represent those quantities. Be specific about what the variables represent and include units.
Step 4: Translate: Translate into a system of equations by writing two linear equations that describe two separate linear relationships found in the problem.
Step 5: Solve: Solve the system of equations using either substitution or elimination.
Step 6: Check: Check the answers in the problem and make sure they makes sense.
Step 7: Answer: Answer the question and be sure to include units on the answers.

Subsection 5.4.2 Translating to a System of Equations

Many times the challenge of solving application problems is being able to translate the situations into algebraic equations. When trying to solve application problems using systems of equations, students often make the mistake of trying to combine the two separate relationships that are present in the situation. The key is to determine what the two separate relationships are and then to keep in mind that these two relationships will be the basis of the two equations that will make up your system.

Let's look at a couple of examples, where we will simply translate each problem into a system of linear equations, using steps 1-4 from the list of strategies above. We will not worry about solving these problems.

Example 5.4.3.

Translate to a system of equations: A married couple together earns $110,000 a year. The wife earns $16,000 less than twice what her husband earns. What does the husband earn? What does the wife earn?

Here, we'll use steps 1-4 from the list of strategies given above.

Step 1:

Read the problem. Make sure you understand all the words and ideas.

This is a problem relating the annual salaries of two people.

Together they make a total of $110,000 annually and the wife makes $16,000 less than two times the husband's salary.

Step 2:

Identify what you are looking for.

"What does the husband earn? What does the wife earn?"

We need to find how much the husband earns and how much the wife earns, per year.

Step 3:

Name what you are looking for by choosing variables to represent those quantities.

We will use two variables, $h$ and $w\text{.}$

Let $h$ represent the husband's annual salary, in dollars, and let $w$ represent the wife's annual salary, in dollars.

Step 4:

Translate into a system of equations.

We will write one equation for each sentence.

\begin{equation*} \underbrace{\text{Together their total annual salary }}_{h+w}\underbrace{\text{is}}_{=}\underbrace{\text{\$110,000}}_{110000} \end{equation*}

\begin{equation*} \underbrace{\text{The wife's annual salary}}_{w}\underbrace{\text{is}}_{=}\underbrace{\text{\$16,000 less than 2 times the husband's salary}}_{2h-16000} \end{equation*}

\begin{equation*} \text{Here is our system of equations:} \end{equation*}

\begin{equation*} \left\{ \begin{alignedat}{4} h {}+{} w {}={} 110000 \\ w {}={} 2h {}-{} 16000 \end{alignedat} \right. \end{equation*}

Example 5.4.4.

Translate to a system of equations: Randall has 125 feet of fencing to enclose a rectangular portion of his backyard adjacent to his house. He will only need to fence around three sides because the fourth side will be the wall of his house. He wants the length of the fenced yard (parallel to the house wall) to be 5 feet more than four times as long as the width. Find the length and the width.

Explanation

Again, we'll use the same steps 1-4 from the list of strategies that we used in the last example.

Step 1:

Read the problem. Make sure you understand all the words and ideas. Sometimes, it may help to make a drawing.

This is a geometric problem involving the three sides of a rectangle - two widths and one length.

It will take a total of 125 feet of fencing to fence two widths and one length of the rectangular yard. The length of the yard must be 5 feet more than four times the width.

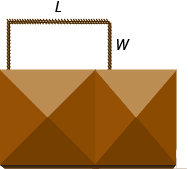
A drawing of a house, from above, with a three-sided fence adjacent to the house.

Step 2:

Identify what you are looking for.

"Find the length and the width."

We need to find the length and the width of the rectangular yard, in feet.

Step 3:

Name what you are looking for by choosing variables to represent those quantities.

We will use two variables, $L$ and $W\text{.}$

Let $L$ represent the length of the rectangle, in feet, and let $W$ represent its width, in feet.

Step 4:

Translate into a system of equations.

We will write one equation for each relationship described in Step 1.

It will take a total of 125 feet of fencing to fence two widths and one length of the rectangular yard.

\begin{equation*} 125=2W+L \end{equation*}

The length of the yard must be 5 feet more than four times the width.

\begin{equation*} L=4W+5 \end{equation*}

Here is our system of equations:

\begin{equation*} \left\{ \begin{alignedat}{4} 125\amp {}={} \amp 2W\amp {}+{} \amp L \\ L\amp {}={} \amp 4W \amp {}+{} \amp 5 \end{alignedat} \right. \end{equation*}

Try a similar exercise.

Checkpoint 5.4.5.

Subsection 5.4.3 Direct Translation Applications

In the previous examples, we learned how to translate application problems into systems of linear equations, but we didn't actually solve those problems. Now we'll translate a situation to a system of equations and then solve the system, using what we learned in Section 5.2 and Section 5.3.

Example 5.4.6.

Translate to a system of equations and then solve: Devon is 26 years older than his son Cooper. The sum of their ages is 50. Find their ages.

Here we'll use our 7-step strategy for solving application problems using a system of linear equations:

Step 1:

Read the problem.

Devon is 26 years older than his son Cooper. The sum of their ages is 50. Find their ages.

Step 2:

Identify what we are looking for.

We are looking for the ages of Devon and Cooper.

Step 3:

Name what we are looking for.

Let $d$ represent Devon's age, in years, and $c$ represent Cooper's age, in years.

Step 4:

Translate into a system of equations.

Devon is 26 years older than Cooper:

\begin{equation*} d=c+26 \end{equation*}

The sum of their ages is 50:

\begin{equation*} d+c=50 \end{equation*}

Thus, the system is:

\begin{equation*} \left\{ \begin{alignedat}{4} d\amp {}={} \amp c\amp {}+{} \amp 26 \\ d\amp {}+{} \amp c \amp {}={} \amp 50 \end{alignedat} \right. \end{equation*}

Step 5:

Solve the system.

We'll use substitution since $d$ is isolated in the first equation.

Substitute $c+26$ for $d$ into the second equation.

\begin{equation*} (\substitute{c+26})+c=50 \end{equation*}

Simplify and solve for $c\text{.}$

\begin{gather*} 2c+26=50\\ 2c+24\\ c=12 \end{gather*}

Substitute $c=12$ into the first equation and then solve for $d\text{.}$

\begin{gather*} d=\substitute{12}+26\\ d=38 \end{gather*}

Step 6:

Check the answer in the problem.

Is Devon's age 26 more than Cooper's? Yes, 38 is 26 more than 12. Is the sum of their ages 50? Yes, 38 plus 12 is 50.

Step 7:

Answer the question.

Devon is 38 and Cooper is 12 years old.

Example 5.4.7.

Translate to a system of equations and then solve: Abdul has $16$ bills in his pocket. Some are $\$5$ bills and some are $\$10$ bills. He has a total of $\$135$ in his pocket. How many of each type of bill does Abdul have in his pocket?

Explanation

Here we'll use our 7-step strategy for solving application problems using a system of linear equations:

Step 1:

Read the problem.

Abdul has $16$ bills in his pocket. Some are $\$5$ bills and some are $\$10$ bills. He has a total of $\$135$ in his pocket. How many of each type of bill does Abdul have in his pocket?

Step 2:

Identify what we are looking for.

We are looking for how many $\$5$ bills and how many $\$10$ bills Abdul has in his pocket.

Step 3:

Name what we are looking for.

Let $x$ represent the number of $\$5$ bills and $y$ represent the number of $\$10$ bills.

Step 4:

Translate into a system of equations.

Abdul has $16$ bills in his pocket:

\begin{equation*} x+y=16 \end{equation*}

He has a total of $\$135$ in his pocket:

\begin{equation*} 5x+10y=135 \end{equation*}

Thus, the system is:

\begin{equation*} \left\{ \begin{alignedat}{4} x\amp {}+{} \amp y\amp {}={} \amp 16 \\ 5x\amp {}+{} \amp 10y \amp {}={} \amp 135 \end{alignedat} \right. \end{equation*}

Step 5:

Solve the system.

We'll use elimination since we can easily eliminate the $x$'s by multiplying each side of the first equation by $-5\text{.}$

Multiply each side of the first equation by $-5$ and simplify.

\begin{gather*} -5(x+y)=-5(16)\\ -5x-5y=-80 \end{gather*}

Add the new first equation to the second equation. Then, solve for $y\text{.}$

\begin{align*} \begin{aligned}-5x-5y\\{}+5x+10y\end{aligned}\amp=\begin{aligned}-80\\{}+135\end{aligned} \end{align*}

So we have

\begin{gather*} 5y=55\\ y=11 \end{gather*}

Substitute $y=11$ into the first equation and then solve for $x\text{.}$

\begin{gather*} x+\substitute{11}=16\\ x=5 \end{gather*}

Step 6:

Check the answer in the problem.

Is the total number of bills 16? Yes, $11$ plus $5$ is $16\text{.}$ Is the total value of the bills $\$135\text{?}$ Yes, $5$ times $\$5$ gives us $\$25\text{,}$ $11$ times $\$10$ equals $\$110\text{,}$ and $\$25+\$110=\$135\text{.}$

Step 7:

Answer the question.

Abdul has $5$ $\$5$ bills and $11$ $\$10$ bills in his pocket.

Try a similar exercise.

Checkpoint 5.4.8.

Let's look at a couple more examples

Example 5.4.9.

A college used to have a north campus with $6000$ students and a south campus with $15{,}000$ students. The percentage of students at the north campus who self-identify as LGBTQ was three times the percentage at the south campus. After the merge, $5.5\%$ of students identify as LGBTQ. What percentage of students on each campus identified as LGBTQ before the merge?

Explanation

We will define $N$ as the percentage (as a decimal) of students at the north campus and $S$ as the percentage (as a decimal) of students at the south campus that identified as LGBTQ. Since the percentage of students at the north campus was three times the percentage at the south campus, we have:

\begin{equation*} N=3S \end{equation*}

For our second equation, we will count LGBTQ students at the various campuses. At the north campus, multiply the population, $6000\text{,}$ by the percentage $N$ to get $6000N\text{.}$ This must be the actual number of LGBTQ students. Similarly, the south campus has $15000S$ LGBTQ students, and the combined school has $21000(0.055)=1155\text{.}$ When we combine the two campuses, we have:

\begin{equation*} 6000N+15000S=1155 \end{equation*}

We write the system as:

\begin{equation*} \left\{ \begin{aligned} N\amp=3S \\ 6000N+15000S\amp=1155 \end{aligned} \right. \end{equation*}

Because the first equation is already solved for $N\text{,}$ this is a good time to use the subsitution method. We can substitute $N$ in our second equation with $3S$ and solve for $S\text{:}$

\begin{align*} 6000N+15000S\amp=1155\\ 6000(\substitute{3S})+15000S\amp=1155\\ 18000S+15000S\amp=1155\\ 33000S\amp=1155\\ \divideunder{33000S}{33000}\amp=\divideunder{1155}{33000}\\ S\amp=0.035 \end{align*}

We can determine $N$ using the first equation:

\begin{align*} N\amp=3S\\ N\amp=3(0.035)\\ N\amp=0.105 \end{align*}

Before the merge, $10.5\%$ of the north campus students self-identified as LGBTQ, and $3.5\%$ of the south campus students self-identified as LGBTQ.

Example 5.4.10. Meal Planning.

Javed is on a meal plan and needs to consume $600$ calories and $20$ grams of fat for breakfast. A small avocado contains $300$ calories and $30$ grams of fat. He has bagels that contain $400$ calories and $8$ grams of fat. Write and solve a system of equations to determine how much bagel and avocado would combine to make his target calories and fat.

Explanation

To write this system of equations, we first need to define our variables. Let $A$ be the number of avocados consumed and let $B$ be the number of bagels consumed. Both $A$ and $B$ might be fractions. For our first equation, we will count calories from the avocados and bagels:

\begin{equation*} \left(300\,\tfrac{\text{calories}}{\text{avocado}}\right)(A\,\text{avocados})+\left(400\,\tfrac{\text{calories}}{\text{bagel}}\right)(B\,\text{bagel})=600\,\text{calories} \end{equation*}

Or, without the units:

\begin{equation*} 300A+400B=600 \end{equation*}

Similarly, for our second equation, we will count the grams of fat:

\begin{equation*} \left(30\,\tfrac{\text{g fat}}{\text{avocado}}\right)(A\,\text{avocados})+\left(8\,\tfrac{\text{g fat}}{\text{bagel}}\right)(B\,\text{bagel})=20\,\text{g fat} \end{equation*}

Or, without the units:

\begin{equation*} 30A+8B=20 \end{equation*}

So the system of equations is:

\begin{align*} \left\{ \begin{alignedat}{4} 300A \amp {}+{} \amp 400B \amp {}={} \amp 600 \\ 30A \amp {}+{} \amp 8B \amp {}={} \amp 20 \end{alignedat} \right. \end{align*}

Since none of the coefficients are equal to $1\text{,}$ it will be easier to use the elimination method to solve this system. Looking at the terms $300A$ and $30A\text{,}$ we can eliminate the $A$ variable if we multiply the second equation by $-10$ to get $-300A\text{:}$

\begin{align*} \amp\left\{ \begin{alignedat}{4} 300A \amp {}+{} \amp 400B \amp {}={} 600 \\ \multiplyleft{-10}(30A \amp {}+{} \amp 8B) \amp {}={} \multiplyleft{-10}(20) \end{alignedat} \right.\\ \amp\left\{ \begin{alignedat}{4} 300A \amp {}+{} \amp 400B \amp {}={}\amp 600 \\ -300A \amp {}+{} \amp (-80B) \amp {}={}\amp {-200} \end{alignedat} \right. \end{align*}

When we add the corresponding sides from the two equations together we have:

\begin{align*} \begin{aligned}300A+400B\\{}-300A-80B\end{aligned}\amp=\begin{aligned}600\\{}-200\end{aligned}\\ \end{align*}

So we have:

\begin{align*} 320B\amp=400\\ \divideunder{320B}{320}\amp=\divideunder{400}{320}\\ B\amp=\frac{5}{4} \end{align*}

We now know that Javed should eat $\frac{5}{4}$ bagels (or one and one-quarter bagels). To determine the number of avocados, we will substitute $B$ with $\frac{5}{4}$ in either of our original equations.

\begin{align*} 300A+400B\amp=600\\ 300A+400\left(\substitute{\frac{5}{4}}\right)\amp=600\\ 300A+500\amp=600\\ 300A\amp=100\\ \divideunder{300A}{300}\amp=\divideunder{100}{300}\\ A\amp=\frac{1}{3} \end{align*}

To check this result, try using $B=\frac{5}{4}$ and $A=\frac{1}{3}$ in each of the original equations:

\begin{align*} 300A+400B\amp=600\amp 30A+8B\amp=20\\ 300\left(\substitute{\frac{1}{3}}\right)+400\left(\substitute{\frac{5}{4}}\right)\amp\stackrel{?}{=}600\amp30\left(\substitute{\frac{1}{3}}\right)+8\left(\substitute{\frac{5}{4}}\right)\amp\stackrel{?}{=}20\\ 100+500\amp\stackrel{\checkmark}{=}600\amp10+10\amp\stackrel{\checkmark}{=}20 \end{align*}

In summary, Javed can eat $\frac{5}{4}$ of a bagel (so one and one-quarter bagel) and $\frac{1}{3}$ of an avocado in order to consume exactly $600$ calories and $20$ grams of fat.

Subsection 5.4.4 Geometry Applications

For geometry applications, you will often use a geometry formula, which can be found in Section 2.2, to write at least one of the equations for your system. Here we will also use some new geometric concepts, which are not found in that section.

Definition 5.4.11. Complementary and Supplementary Angles.

Two angles are complementary if the sum of the measures of their angles is $90$ degrees. Two angles are supplementary if the sum of the measures of their angles is $180$ degrees. If two angles are complementary, we say that one angle is the complement of the other. If two angles are supplementary, we say that one angle is the supplement of the other.

Example 5.4.12.

Translate to a system of equations and then solve: The difference of two complementary angles is $26$ degrees. Find the measures of the angles.

Here we'll use our 7-step strategy for solving application problems using a system of linear equations:

Step 1:

Read the problem.

The difference of two complementary angles is $26$ degrees. Find the measures of the angles.

Step 2:

Identify what we are looking for.

We are looking for the measure of each of the two angles.

Step 3:

Name what we are looking for.

Let $x$ represent the measure of the larger angle, in degrees, and $y$ represent the measure of the smaller angle, in degrees.

Step 4:

Translate into a system of equations.

The two angles are complementary angles, which means the sum of the measures of their angles is $90$ degrees:

\begin{equation*} x+y=90 \end{equation*}

The difference of the two angles is $26$ degrees:

\begin{equation*} x-y=26 \end{equation*}

Thus, the system is:

\begin{equation*} \left\{ \begin{alignedat}{4} x\amp {}+{} \amp y\amp {}={} \amp 90 \\ x\amp {}-{} \amp y \amp {}={} \amp 26 \end{alignedat} \right. \end{equation*}

Step 5:

Solve the system.

We'll use elimination since we can see that adding these equations together, as they are, will eliminate the $y$'s.

Add the first equation to the second equation. Then, solve for $x\text{.}$

\begin{align*} \begin{aligned}x+y\\{}+x-y\end{aligned}\amp=\begin{aligned}90\\{}+26\end{aligned} \end{align*}

So we have

\begin{gather*} 2x=116\\ x=58 \end{gather*}

Substitute $x=58$ into the first equation and then solve for $y\text{.}$

\begin{gather*} \substitute{58}+y=90\\ y=32 \end{gather*}

Step 6:

Check the answer in the problem.

Do their measures add to $90$ degrees? Yes, $58$ plus $32$ is $90\text{.}$ Is their difference $26\text{?}$ Yes, $58$ minus $32$ is $26\text{.}$

Step 7:

Answer the question.

The measures of the two complementary angles are $58$ degrees and $32$ degrees.

Try a similar exercise.

Checkpoint 5.4.13.

Example 5.4.14.

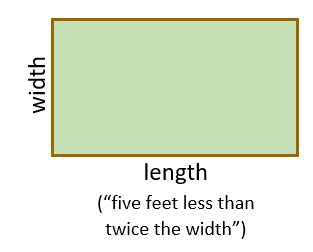
Translate to a system of equations and then solve: Hyosun wants to fence a rectangular garden, using $260$ feet of fencing. She'd like the length of the garden to be five feet less than twice the width. Find the dimensions of the garden.

Explanation

Here we'll use our 7-step strategy for solving application problems using a system of linear equations:

Step 1:

Read the problem. Draw a picture or diagram, if applicable.

Hyosun wants to fence a rectangular garden, using $260$ feet of fencing. She'd like the length of the garden to be five feet less than twice the width.

Find the dimensions of the garden. Draw a diagram:

A drawing of a rectangular garden, from above, with one short side marked as "width" and a long side marked as "length (five feet less than twice the width)".

Step 2:

Identify what we are looking for.

We are looking for the length and width of the rectangular garden.

Step 3:

Name what we are looking for.

Let $L$ represent the length, in feet, and $W$ represent the width, in feet, of the rectangular garden.

Step 4:

Translate into a system of equations.

She'd like the length of the garden to be five feet less than twice the width:

\begin{equation*} L=2W-5 \end{equation*}

She has a total of $260$ feet of fencing to use to fence the rectangular garden. Since the fencing will be used to outline the perimeter of the garden,

we need to use the perimeter formula for a rectangle, $P=2L+2W\text{,}$ and plug in $260$ for $P\text{.}$ This gives us our second equation:

\begin{equation*} 260=2L+2W \end{equation*}

Thus, the system is:

\begin{equation*} \begin{cases} L=2W-5 \\ 260=2L+2W \end{cases} \end{equation*}

Step 5:

Solve the system.

We'll use substitution since the first equation is already solved for $L\text{.}$

Substitute the expression $2W-5$ in place of $L$ in the second equation. Then, solve for $W\text{.}$

\begin{gather*} 260=2(\substitute{2W-5})+2W \end{gather*}

So we have

\begin{gather*} 260=4W-10+2W\\ 260=6W-10\\ 270=6W\\ W=45 \end{gather*}

Substitute $W=45$ into the first equation and then solve for $L\text{.}$

\begin{gather*} L=2(\substitute{45})-5\\ L=90-5\\ L=85 \end{gather*}

Step 6:

Check the answer in the problem.

Do the four sides add to $260$ feet? Yes, $45+85+45+85=260\text{.}$ Is the length five feet less than twice the width? Yes, twice $45$ feet is $90$ feet and $90$ feet minus $5$ feet is $85$ feet.

Step 7:

Answer the question.

The length of the rectangular garden is $85$ feet and its width is $45$ feet.

Try a similar exercise.

Checkpoint 5.4.15.

Subsection 5.4.5 Uniform Motion Applications

The basic equation we use in uniform motion problems is $d=rt$ where $d$ is the distance traveled, $r$ is the rate or speed at which the person or object is traveling, and $t$ is the time the person or object has traveled. For these problems, we will learn how to use a table to organize our information, which will help us to translate the situation into a system of equations.

Example 5.4.16.

Translate to a system of equations and then solve: Joni left St. Louis on the interstate, driving west toward Denver at a speed of 65 miles per hour. Half an hour later, Kelly left St. Louis on the same route as Joni, driving 78 miles per hour. How long will it take Kelly to catch up to Joni?

A diagram is useful in helping us visualize the situation.

A diagram with "Denver" on the left and "St. Louis" on the right. Then, two arrows pointing from St. Louis to Denver, one Labeled with "Joni" and the other with "Kelly (1/2 hour later)" and speeds of 65 mph and 78 mph labeled on each arrow respectively. — Figure 5.4.17.

Identify and name what we are looking for. A table will help us organize the information. We know the rates of both Joni and Kelly, and so we enter them in the table. We don't know how long they have been driving at those rates, so we will let $j$ represent Joni's time, in hours, and let $k$ represent Kelly's time, in hours, and enter that information into the table as well. Then, we can multiply the rates and times together to obtain an expression for each person's distance.

A table with column headings of type, rate, time, and distance. The types are Joni and Kelly. The rates are 65 and 78. The times are variables j and k. The distances are 65j and 78j. — Figure 5.4.18.

Translate into a system of equations. To make the system of equations, we must recognize that Kelly and Joni will drive the same distance. So, $65j=78k\text{.}$

Also, since Kelly left later, her time will be $\frac{1}{2}$ hour less than Joni's time. So, $k=j-\frac{1}{2}\text{.}$ Now we have a system:

\begin{align*} \left\{ \begin{alignedat}{4} 65j\amp {}={} \amp 78k \\ k\amp {}={} j \amp {}-{} \amp \frac{1}{2} \end{alignedat} \right. \end{align*}

Solve the system of equations, either by substitution or elimination. This system, lends itself easily to substitution since $k$ is already isolated in the second equation. Thus, we can substitute the expression $j-\frac{1}{2}$ in place of $k$ in the first equation:

\begin{gather*} 65j=78\left(\substitute{j-\frac{1}{2}}\right)\\ 65j=78j-39\\ -13j=-39\\ j=3 \end{gather*}

Substitute $3$ for $j$ in the second equation and solve for $k\text{:}$

\begin{gather*} k=\substitute{3}-\frac{1}{2}\\ k=2.5 \end{gather*}

Therefore, it will take Kelly $2.5$ hours to catch up to Joni. The check is left to the reader.

Try a similar exercise.

Checkpoint 5.4.19.

Many real-world applications of uniform motion arise because of the effects of currents - of water or air - on the actual speed of a vehicle. For example, cross-country airplane flights in the United States generally take longer going west than going east because of the prevailing wind currents.

Let's take a look at a boat traveling on a river. Depending on which way the boat is going, the curent of the water is either slowing it down or speeding it up.

Figure 5.4.20 and Figure 5.4.21 show how a river current affects the speed at which a boat is actually traveling. We'll call the speed of the boat in still water $b$ and the speed of the river current $c\text{.}$

In Figure 5.4.20 the boat is going downstream, in the same direction as the river current. The current helps push the boat, so the boat's actual speed is faster than its speed in still water. The actual speed at which the boat is moving is $b+c\text{.}$

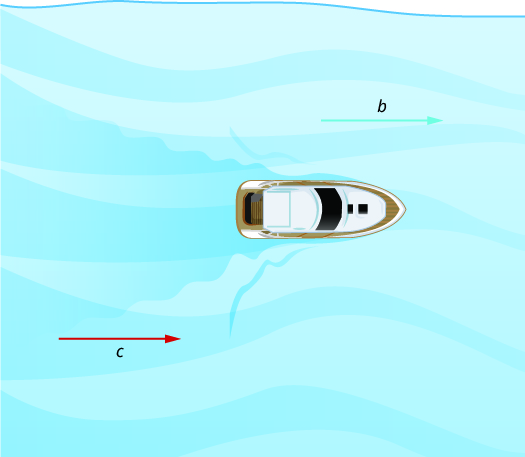
A picture of a boat traveling downstream, with the current. — Figure 5.4.20.

In Figure 5.4.21 the boat is going upstream, opposite the river current. The current is going against the boat, so the boat's actual speed is slower than its speed in still water. The actual speed of the boat is $b-c\text{.}$

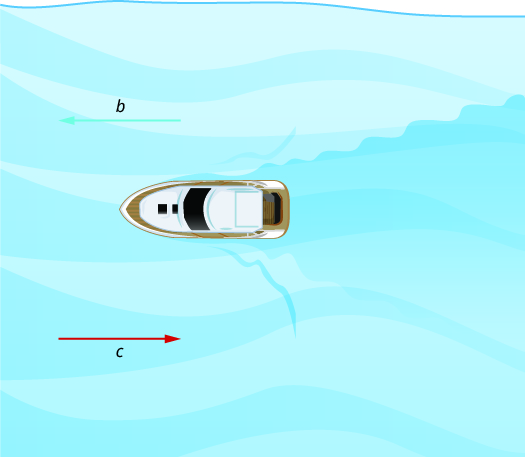
A picture of a boat traveling upstream, against the current. — Figure 5.4.21.

We'll put some numbers to this situation in the next example.

Example 5.4.22.

Translate to a system of equations and then solve: A river cruise ship sailed $60$ miles downstream for $4$ hours and then took $5$ hours sailing upstream to return to the dock. Find the speed of the ship in still water and the speed of the current.

A diagram is useful in helping us visualize the situation.

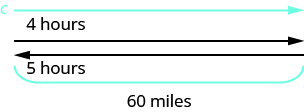
A diagram showing two arrows pointing in opposite directions, to represent a boat traveling one direction and then traveling back in the opposite direction the same distance. Then one blue arrow represents the direction of the current of the river. — Figure 5.4.23.

Identify and name what we are looking for. A table will help us organize the information, including the use of the formula $d=rt\text{.}$ We know the times of both trips downstream and upstream, and so we enter those times in the table. We also know that the distance for both trips is $60$ miles, so we can also enter that information into the table. We don't know the ship's speed in still water or the speed of the current, so we will let $s$ represent the ship's speed, in miles per hour, in still water and let $c$ represent the speed of the current, in miles per hour.

As explained previously, when the ship is going downstream, the current will push the ship faster, so the rate at which the ship is traveling can be represented by $s+c\text{.}$ When the ship is going upstream, the current will slow the ship down, so the rate at which the ship will be traveling can be represented by $s-c\text{.}$ We can now enter that information into the table as well.

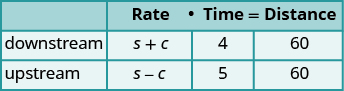
A table with column headings of rate, time, and distance, as well as row headings of downstream and upstream. The rates are s+c and s-c. The times are 4 and 5. The distances are both 60. — Figure 5.4.24.

Translate into a system of equations. To make the system of equations, we use the fact that the product of the rate and the time is equal to the distance for each trip. This will give us our two equations:

\begin{equation*} \begin{cases} 4(s+c)=60\\5(s-c)=60 \end{cases} \end{equation*}

Solve the system of equations, either by substitution or elimination. The first thing to do is simplify each equation by using the distributive property to get rid of the parentheses:

\begin{equation*} \begin{cases} 4s+4c=60\\5s-5c=60 \end{cases} \end{equation*}

Since all the variable terms have a coefficient (not equal to one), the best method to use to solve this system is the elimination method.

Notice that the $c$ terms already have opposite signs, so we'll work to eliminate the variable $c\text{.}$ The least common mutiple of $4$ and $5$ is $20\text{,}$ so if we multiply both sides of the first equation by $5$ and both sides of the second equation by $4\text{,}$ then the new $c$ terms will be $20c$ and $-20c$ respectively, which eliminate the $c$ terms when the new equations are added together.

Multiply both sides of the first equation by $5$ and both sides of the second equation by $4\text{:}$

\begin{gather*} 5(4s+4c)=5(60)\\ 4(5s-5c)=4(60) \end{gather*}

Now, our new system is:

\begin{equation*} \begin{cases} 20s+20c=300\\20s-20c=240 \end{cases} \end{equation*}

Add the first equation to the second equation. Then, solve for $s\text{.}$

\begin{align*} \begin{aligned}20s+20c\\{}+20s-20c\end{aligned}\amp=\begin{aligned}300\\{}+240\end{aligned} \end{align*}

So we have

\begin{gather*} 40s=540\\ s=13.5 \end{gather*}

Substitute $13.5$ for $s$ in the first original equation and solve for $c\text{:}$

\begin{gather*} 4(\substitute{13.5}+c)=60\\ 54+4c=60\\ 4c=6\\ c=1.5 \end{gather*}

Therefore, the ship's speed in still water is $13.5$ miles per hour and the speed of the current is $1.5$ miles per hour. The check is left to the reader.

Try a similar exercise

Checkpoint 5.4.25.

Example 5.4.26.

Translate to a system of equations and then solve: A private jet can fly $1095$ miles in three hours with a tailwind, but only $987$ miles into a headwind in the same amount of time. Find the speed of the jet in still air and the speed of the wind.

Explanation

A diagram is useful in helping us visualize the situation.

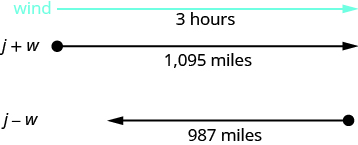
A diagram showing two arrows pointing in opposite directions, to represent a jet traveling one direction for a distance of 1095 miles and then traveling back in the opposite direction for a distance of 987 miles. Then one blue arrow represents the direction of the wind, with the time of 3 hours labeled on that arrow, representing the time traveled by the jet in both directions. There are also expressions of "j+w" labeling the arrow that represents the 1095-mile trip and "j-w" labeling the arrow that represents the 987-mile trip.

Identify and name what we are looking for. A table will help us organize the information, including the use of the formula $d=rt\text{.}$ The time of both trips is given to be three hours and so we enter that time in the table, in the appropriate spots. We also know the distances for each trip, which is $1095$ miles with a tailwind and $987$ miles into a headwind, so we can also enter that information into the table. We don't know the jet's speed in still air or the speed of the wind, so we will let $j$ represent the jet's speed in still air and let $w$ represent the speed of the wind, both in miles per hour.

Note that when the jet is flying with the tailwind, that means the wind will be pushing the jet faster than it would be going in still air, so we can represent its rate with the tailwind as $j+w\text{.}$ In contrast, when the jet is flying into the tailwind, the wind will slow the jet down, making it go slower than it would be traveling in still air, so we can represent its rate into the tailwind as $j-w\text{.}$ These expressions can then be entered into the table for each rate.

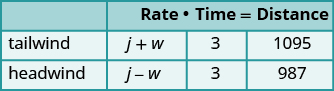
A table with column headings of rate, time, and distance, as well as row headings of tailwind and headwind. The rates are j+w and j-w. The times are both 3. The distances are 1095 for tailwind and 987 for headwind.

\begin{equation*} \begin{cases} \multiplyleft{3}(j+w)=1095\\\multiplyleft{3}(j-w)=987 \end{cases} \end{equation*}

Solve the system of equations, either by substitution or elimination. The first thing to do is simplify each equation by using the distributive property to get rid of the parentheses:

\begin{equation*} \begin{cases} 3j+3w=1095\\3j-3w=987 \end{cases} \end{equation*}

The best method to use to solve this system is the elimination method since the $w$ terms of the two equations add to zero.

Add the first equation to the second equation. Then, solve for $j\text{.}$

\begin{align*} \begin{aligned}3j+3w\\{}+3j-3w\end{aligned}\amp=\begin{aligned}1095\\{}+987\end{aligned} \end{align*}

So we have

\begin{gather*} 6j=2082\\ j=347 \end{gather*}

Substitute $347$ for $j$ in the first original equation and solve for $w\text{:}$

\begin{gather*} 3(\substitute{347}+w)=1095\\ 1041+3w=1095\\ 3w=54\\ w=18 \end{gather*}

Therefore, the jet's speed in still air is $347$ miles per hour and the speed of the wind is $18$ miles per hour. The check is left to the reader.

Try a similar exercise

Checkpoint 5.4.27.

Subsection 5.4.6 Mixture Applications

Some mixture applications involve combining foods or drinks. Example situations might include combining raisins and nuts to make a trail mix or using two types of coffee beans to make a blend.

Example 5.4.28. Combining Foods with Different Costs.

Translate to a system of equations and solve: Carson wants to make $20$ pounds of trail mix using nuts and chocolate chips. His budget requires that the trail mix costs him $\$7.60$ per pound. Nuts cost $\$9.00$ per pound and chocolate chips cost $\$2.00$ per pound. How many pounds of nuts and how many pounds of chocolate chips should he use?

Explanation

Read the problem. We will create a table to organize the information. Note that with mixture problems, when mixing two ingredients, we will have one row for each ingredient and one total row for the final mixture, giving us three rows in our table.

Identify what we are looking for. We are looking for the number of pounds of nuts and the number of pounds of chocolate chips.

Name what we are looking for. Let $n$ represent the number of pounds of nuts he needs and $c$ represent the number of pounds of chocolate chips he needs.

Carson will mix nuts and chocolate chips to get trail mix. Write in $n$ and $c$ in the table for the number of pounds of nuts and chocolate chips. There will be $20$ pounds of trail mix.

Put the price per pound of each item in the Value column. Fill in the last column using $\text{Number of Pounds}\cdot\text{Value}=\text{Total Value}\text{:}$

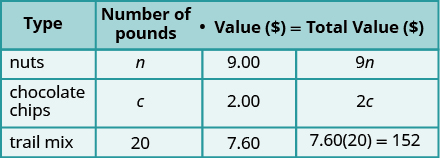
A table with column headings type, number of pounds, value, and total value. The types are nuts, chocolate chips, and trail mix. The number of pounds are n, c, and 20. The values are 9.00, 2.00, and 7.60. The total values are 9n, 2c, and 7.60(20)=152.

Translate into a system of equations. Note that an advantage of setting up the table this way, in mixture problems, is that the first and last columns will always give us the two equations we need for our system, where the cells in the first two rows must always add to the last cell in the total row. So we get the two equations for our system from the Number of Pounds column and the Total Value column:

\begin{equation*} \begin{cases}n+c=20\\9n+2c=152 \end{cases} \end{equation*}

Solve the system of equations. We will use elimination to solve the system.

Multiply the first equation by $-2$ to eliminate $c\text{.}$

\begin{gather*} \multiplyleft{-2}(n+c)=\multiplyleft{-2}(20)\\ 9n+2c=152 \end{gather*}

Simplify and add. Then solve for n.

\begin{align*} \begin{aligned}-2n-2c\\{}+9n+2c\end{aligned}\amp=\begin{aligned}-40\\{}+152\end{aligned} \end{align*}

So we have

\begin{gather*} 7n=112\\ n=16 \end{gather*}

To find the number of pounds of chocolate chips, substitute $n=16$ into the first equation, then solve for $c\text{.}$

\begin{gather*} n+c=20\\ \substitute{16}+c=20\\ c=4 \end{gather*}

Check the answer in the problem.

\begin{equation*} 16+4=20\text{? Yes!} \end{equation*}

\begin{gather*} 9(16)+2(4)=152\text{?}\\ 144+8=152\text{? Yes!} \end{gather*}

Answer the question. Carson should mix $16$ pounds of nuts with $4$ pounds of chocolate chips to create the trail mix.

Try a similar exercise.

Checkpoint 5.4.29.

Example 5.4.30. Mixing Solutions with Two Different Concentrations.

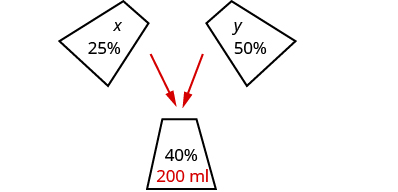
Sasheena is a lab assistant at her community college. She needs to make $200$ milliliters of a $40\%$ solution of sulfuric acid for a lab experiment. The lab has only $25\%$ and $50\%$ solutions in the storeroom. How much should she mix of the $25\%$ and the $50\%$ solutions to make the $40\%$ solution?

Read the problem. A figure may help us visualize the situation, then we will create a table to organize the information.

Sasheena must mix some of the $25\%$ solution and some of the $50\%$ solution together to create $200$mL of the $40\%$ solution.

Diagram of a container marked with x and 25%, plus a container marked with y and 50%, both with arrows point down toward a third container marked with 40% and 200 ml.

Name what we are looking for.

The two unknowns are the amount of each type of solution being mixed together. Let $x$ represent the amount of $25\%$ solution (in mL) and let $y$ represent the amount of $50\%$ solution (in mL). One quantity given to us in the problem is 200 mL, which is the amount of the $40\%$ solution that needs to be created.

These three amounts, as well as the concentrations for each type of solution, can be entered into the table and then the amount of sulfuric acid in each type of solution can be calculated by multiplying the number of milliters of solution times the concentration (in decimal form).

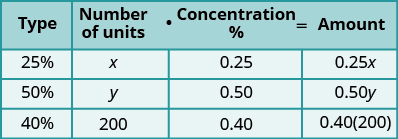
$A table with column headings of type, number of units, concentration(\%), and amount. For the types, there are 25\%, 50\%, and 40\%. The number of units are x, y, and 200. The amounts are 0.25x, 0.50y, and 0.40(200).$

Translate into a system of equations. Since $200$mL is the total volume of the $40\%$ solution, we must have for one of the equations in the system:

\begin{equation*} (x\,\text{mL})+(y\,\text{mL})=200\,\text{mL} \end{equation*}

Or without units:

\begin{equation*} x+y=200 \end{equation*}

To build the second equation, we have to think about the amount (in mL) of sulfuric acid being mixed. If we have $x$ milliliters of solution that is $25\%$ sulfuric acid, then $0.25x$ is the actual amount (in mL) of sulfuric acid in that solution. Similarly, $0.50y$ is the amount of sulfuric acid in the $50\%$ solution. The final solution is 200 mL of solution that is $40\%$ sulfuric acid, so it has $0.40(200)=80$mL of sulfuric acid. All of this together means:

\begin{equation*} 0.25(x\,\text{mL})+0.50(y\,\text{mL})=80\,\text{mL} \end{equation*}

Or without units:

\begin{equation*} 0.25x+0.50y=80 \end{equation*}

So our system is:

\begin{equation*} \left\{ \begin{alignedat}{3} x\amp+{}\amp y\amp=200 \\ 0.25x\amp+{}\amp0.50y\amp=80 \end{alignedat} \right. \end{equation*}

Solve the system of equations. To solve this system, we'll solve for $x$ in the first equation:

\begin{align*} x+y\amp=200\\ x\amp=200-y \end{align*}

And then substitute $x$ in the second equation with $200-y\text{:}$

\begin{align*} 0.25x+0.50y\amp=80\\ 0.25(\substitute{200-y})+0.50y\amp=80\\ 50-0.25y+0.50y\amp=80\\ 50+0.25y\amp=80\\ 0.25y\amp=30\\ \divideunder{0.25y}{0.25}\amp=\divideunder{30}{0.25}\\ y\amp=120 \end{align*}

As a last step, we will determine $x$ using the equation where we had isolated $x\text{:}$

\begin{align*} x\amp=200-y\\ x\amp=200-\substitute{120}\\ x\amp=80 \end{align*}

Check the answer in the problem.

\begin{equation*} 80+120=200\text{? Yes!} \end{equation*}

\begin{gather*} 0.25(80)+0.50(120)=80\text{?}\\ 20+60=80\text{? Yes!} \end{gather*}

Answer the question. In summary, Sasheena needs to combine 80 mL of $25\%$ sulfuric acid solution with 120 mL of $50\%$ sulfuric acid solution to create 200 mL of solution that is $40\%$ sulfuric acid by volume.

Try a similar exercise.

Checkpoint 5.4.31.

Subsection 5.4.7 Interest Applications

The formula to model interest applications is $I=Prt\text{.}$ Interest earned or owed, $I\text{,}$ is the product of the principal, $P\text{,}$ the rate, $r\text{,}$ and the time (in years), $t\text{.}$

In these interest application problems, we'll use a table to organize the information, similar to uniform motion and mixture applications, as you'll see in Example 5.4.32.

Example 5.4.32. Investing at Two Different Interest Rates.

Adrian invested $\$40{,}000$ last year. He put some of the money into a stock fund that earns $8\%$ per year and the rest into bonds that earns $3\%$ per year. If he earned a total of $\$2840$ in interest that year, how much money did he put into each fund?

Read the problem. A table will help us organize the information.

Identify what we are looking for. We are looking for the amount to invest in each fund.

Name what we are looking for. Let $s$ represent the amount, in dollars, invested in a stock fund and let $b$ represent the amount, in dollars, invested in bonds. Write these in the table under Principal for each account.

Write the interest rate (in decimal form) for each fund. We're interested in the amount of interest earned per year, so the time will be $1$ year for both the stock fund and the bonds. Multiply: Principal $\cdot$ Rate $\cdot$ Time to get the Interest for each account as well as the total.

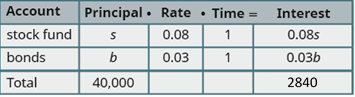
A table with column headings of Account, Principal, Rate, Time, and Interest, and row headings of Stock fund, Bonds, and Total. Under Principal are entries s, b, and 40,000. Under Rate are entries 0.08 and 0.03 (the last cell is blank). Under Time are entries 1 and 1 (the last cell is blank). Under Interest are entries 0.08s, 0.03b, and 2840.

Translate into a system of equations. We get our system of equations from the Principal column and the Interest column, since the amounts invested in each account should add together to equal the total amount invested and the amounts of interest earned in each account added together should equal the total amount of interest earned. So here is our system:

\begin{gather*} \begin{cases} s+b=40{,}000 \\ 0.08s+0.03b=2840 \end{cases} \end{gather*}

Solve the system of equations. We'll solve this by substitution.

Solve the first equation for $b\text{:}$ $b=40{,}000-s\text{.}$

Substitute $40{,}000-s$ in for $b$ in the second equation and solve for $s\text{:}$

\begin{gather*} 0.08s+0.03(\substitute{40{,}000-s})=2840\\ 0.08s+1200-0.03s=2840\\ 0.05s=1640\\ s=32{,}800 \end{gather*}

To find $b\text{,}$ substitute $32{,}800$ in for $s$ in the first equation and solve for $b\text{:}$

\begin{gather*} \substitute{32{,}800}+b=40{,}000\\ b=7200 \end{gather*}

Check the answer in the problem. Do the two amounts invested add to $\$40{,}000\text{?}$ Yes! Will he earn a total of $7.1\%$ interest in one year?

\begin{gather*} 0.08(\substitute{32{,}800})+0.03(\substitute{7200})=0.071(40{,}000)\text{ ?}\\ 2624+216=2840\text{ ? Yes!} \end{gather*}

Answer the question. Adrian invested $\$32{,}800$ in the stock fund and $\$7200$ in bonds.

Example 5.4.33. Owing at Two Different Rates.

Notah made some large purchases with his two credit cards one month and took on a total of $\$8{,}400$ in debt from the two cards. He didn't make any payments the first month, so the two credit card debts each started to accrue interest. That month, his Visa card charged $2\%$ interest and his Mastercard charged $2.5\%$ interest. Because of this, Notah's total debt grew by $\$178\text{.}$ How much money did Notah charge to each card?

Explanation

To start, we will define two variables based on our two unknowns. Let $v$ be the amount charged to the Visa card (in dollars) and let $m$ be the amount charged to the Mastercard (in dollars).

To determine our equations, notice that we are given two different totals. We will use these to form our two equations. The total amount charged is $\$8{,}400$ so we have:

\begin{equation*} (v\,\text{dollars})+(m\,\text{dollars})=\$8400 \end{equation*}

Or without units:

\begin{equation*} v+m=8400 \end{equation*}

The other total we were given is the total amount of interest, $\$178\text{,}$ which is also in dollars. The Visa had $v$ dollars charged to it and accrues $2\%$ interest. So $0.02v$ is the dollar amount of interest that comes from using this card. Similarly, $0.025m$ is the dollar amount of interest from using the Mastercard. Together:

\begin{equation*} 0.02(v\,\text{dollars})+0.025(m\,\text{dollars})=\$178 \end{equation*}

Or without units:

\begin{equation*} 0.02v+0.025m=178 \end{equation*}

As a system, we write:

\begin{equation*} \left\{ \begin{alignedat}{3} v\amp+{}\amp m\amp={}8400 \\ 0.02v\amp+{}\amp 0.025m\amp{}=178 \\ \end{alignedat} \right. \end{equation*}

To solve this system by substitution, notice that it will be easier to solve for one of the variables in the first equation. We'll solve that equation for $v\text{:}$

\begin{align*} v+m\amp=8400\\ v\amp=8400-m \end{align*}

Now we will substitute $8400-m$ for $v$ in the second equation:

\begin{align*} 0.02v+0.025m\amp=178\\ 0.02(\substitute{8400-m})+0.025m\amp=178\\ 168-0.02m+0.025m\amp=178\\ 168+0.005m\amp=178\\ 0.005m\amp=10\\ m\amp=2000 \end{align*}

Lastly, we can determine the value of $v$ by using the earlier equation where we isolated $v\text{:}$

\begin{align*} v\amp=8400-m\\ v\amp=8400-\substitute{2000}\\ v\amp=6400 \end{align*}

In summary, Notah charged $\$6400$ to the Visa and $\$2000$ to the Mastercard. We should check that these numbers work as solutions to our original system and that they make sense in context. (For instance, if one of these numbers were negative, or was something small like $\$0.50\text{,}$ they wouldn't make sense as credit card debt.)

Try a similar exercise

Checkpoint 5.4.34.

Exercises 5.4.8 Exercises

1.

A jar of pennies and nickels has 400 coins. In total, the value of all this money is $12.00. If there are $p$ pennies and $n$ nickels, write two equations that this situation suggests.

2.

A school fund raising event sold a total of $175$ tickets and generated a total revenue of ${\$717.50}\text{.}$ There are two types of tickets: adult tickets and child tickets. Each adult ticket costs ${\$6.35}\text{,}$ and each child ticket costs ${\$3.20}\text{.}$ Write and solve a system of equations to answer the following questions.

adult tickets and child tickets were sold.

3.

Phone Company A charges a monthly fee of ${\$25.60}$, and ${\$0.05}$ for each minute of talk time. Phone Company B charges a monthly fee of ${\$20.00}$, and ${\$0.07}$ for each minute of talk time. Write and solve a system equation to answer the following question.

These two companies would charge the same amount on a monthly bill when the talk time was minutes.

4.

Company A’s revenue this fiscal year is ${\$946{,}000}\text{,}$ but its revenue is decreasing by ${\$12{,}000}$ each year. Company B’s revenue this fiscal year is ${\$414{,}000}\text{,}$ and its revenue is increasing by ${\$16{,}000}$ each year. Write and solve a system of equations to answer the following question.

After years, Company B will catch up with Company A in revenue.

5.

A test has $18$ problems, which are worth a total of $64$ points. There are two types of problems in the test. Each multiple-choice problem is worth $2$ points, and each short-answer problem is worth $6$ points. Write and solve a system equation to answer the following questions.

This test has multiple-choice problems and short-answer problems.

6.

A test has $21$ problems, which are worth a total of $84$ points. There are two types of problems in the test. Each multiple-choice problem is worth $2$ points, and each short-answer problem is worth $9$ points. Write and solve a system of equations to answer the following questions.

This test has multiple-choice problems and short-answer problems.

7.

You will purchase some CDs and DVDs. If you purchase $9$ CDs and $10$ DVDs, it will cost you ${\$121.05}\text{;}$ if you purchase $10$ CDs and $9$ DVDs, it will cost you ${\$113.60}\text{.}$ Write and solve a system of equations to answer the following questions.

Each CD costs and each DVD costs .

8.

A school fund raising event sold a total of $211$ tickets and generated a total revenue of ${\$762.60}\text{.}$ There are two types of tickets: adult tickets and child tickets. Each adult ticket costs ${\$5.65}\text{,}$ and each child ticket costs ${\$2.10}\text{.}$ Write and solve a system of equations to answer the following questions.

adult tickets and child tickets were sold.

9.

Phone Company A charges a monthly fee of ${\$37.50}$, and ${\$0.04}$ for each minute of talk time. Phone Company B charges a monthly fee of ${\$25.00}$, and ${\$0.09}$ for each minute of talk time. Write and solve a system equation to answer the following question.

These two companies would charge the same amount on a monthly bill when the talk time was minutes.

10.

Company A’s revenue this fiscal year is ${\$819{,}000}\text{,}$ but its revenue is decreasing by ${\$10{,}000}$ each year. Company B’s revenue this fiscal year is ${\$531{,}000}\text{,}$ and its revenue is increasing by ${\$8{,}000}$ each year. Write and solve a system of equations to answer the following question.

After years, Company B will catch up with Company A in revenue.

11.

A small fair charges different admission for adults and children. It charges ${\$4}$ for adults, and ${\$1.75}$ for children. On a certain day, the total revenue is ${\$8{,}105}$ and the fair admits ${3500}$ people. How many adults and children were admitted?

There were adults and children at the fair.

12.

A rectangle’s length is $10$ feet shorter than four times its width. The rectangle’s perimeter is $430$ feet. Find the rectangle’s length and width.

The rectangle’s length is feet, and its width is feet.

13.

A rectangle’s length is $10$ feet shorter than twice its width. The rectangle’s perimeter is $100$ feet. Find the rectangle’s length and width.

The rectangle’s length is feet, and its width is feet.

14.

Two angles are complementary. The measure of the larger angle is $6$ degrees more than twice the smaller angle. Find the measures of the angles.

The measure of the larger angle is degrees and the measure of the smaller angle is degrees.

15.

One angle is $70^{\circ}$ more than three times its complement. The measures, in degrees, of the two complementary angles are and .

16.

One angle is $30^{\circ}$ more than four times its supplement. The measures, in degrees, of the two supplementary angles are and .

17.

One angle is $60^{\circ}$ less than seven times its supplement. The measures, in degrees, of the two supplementary angles are and .

18.

Justin's boat travels 92 km downstream in 4 hours and it travels 90 km upstream in 6 hours. Find the speed of the boat in still water and the speed of the stream's current.

Boat Speed: km/h

Current Speed: km/h

19.

If a boat travels from Town A to Town B, it has to travel ${1330\ {\rm mi}}$ along a river. A boat traveled from Town A to Town B along the river’s current with its engine running at full speed. This trip took ${47.5\ {\rm hr}}\text{.}$ Then the boat traveled back from Town B to Town A, again with the engine at full speed, but this time against the river’s current. This trip took ${66.5\ {\rm hr}}\text{.}$ Write and solve a system of equations to answer the following questions.

The boat’s speed in still water with the engine running at full speed is .

The river current’s speed was .

20.

Justin's boat travels 150 km downstream in 5 hours and it travels 176 km upstream in 8 hours. Find the speed of the boat in still water and the speed of the stream's current.

Boat Speed: km/h

Current Speed: km/h

21.

If a boat travels from Town A to Town B, it has to travel ${1963.5\ {\rm mi}}$ along a river. A boat traveled from Town A to Town B along the river’s current with its engine running at full speed. This trip took ${59.5\ {\rm hr}}\text{.}$ Then the boat traveled back from Town B to Town A, again with the engine at full speed, but this time against the river’s current. This trip took ${93.5\ {\rm hr}}\text{.}$ Write and solve a system of equations to answer the following questions.

The boat’s speed in still water with the engine running at full speed is .

The river current’s speed was .

22.

You poured some $8\%$ alcohol solution and some $6\%$ alcohol solution into a mixing container. Now you have $560$ grams of $6.5 \%$ alcohol solution. How many grams of $8\%$ solution and how many grams of $6 \%$ solution did you pour into the mixing container?

Write and solve a system equation to answer the following questions.

You mixed grams of $8\%$ solution with grams of $6\%$ solution.

23.

A store has some beans selling for ${\$2.50}$ per pound, and some vegetables selling for ${\$3.70}$ per pound. The store plans to use them to produce $12$ pounds of mixture and sell for ${\$3.05}$ per pound. How many pounds of beans and how many pounds of vegetables should be used?

To produce $12$ pounds of mixture, the store should use pounds of beans and pounds of vegetables.

24.

You’ve poured some $12\%$ (by mass) alcohol solution and some $10\%$ alcohol solution into a large glass mixing container. Now you have $500$ grams of $10.72\%$ alcohol solution. How many grams of $12\%$ solution and how many grams of $10\%$ solution did you pour into the mixing container?

You poured grams of $12\%$ solution and grams of $10\%$ solution into the mixing container.

25.

You’ve poured some $8\%$ (by mass) alcohol solution and some $10\%$ alcohol solution into a large glass mixing container. Now you have $600$ grams of $9.4\%$ alcohol solution. How many grams of $8\%$ solution and how many grams of $10\%$ solution did you pour into the mixing container?

You poured grams of $8\%$ solution and grams of $10\%$ solution into the mixing container.

26.

A store has some beans selling for ${\$1.00}$ per pound, and some vegetables selling for ${\$4.90}$ per pound. The store plans to use them to produce $13$ pounds of mixture and sell for ${\$3.04}$ per pound. How many pounds of beans and how many pounds of vegetables should be used?

To produce $13$ pounds of mixture, the store should use pounds of beans and pounds of vegetables.

27.

You poured some $6\%$ alcohol solution and some $12\%$ alcohol solution into a mixing container. Now you have $720$ grams of $9 \%$ alcohol solution. Write and solve a system of equations to find how many grams of $6\%$ solution and how many grams of $12 \%$ solution you poured into the mixing container.

You mixed grams of $6\%$ solution with grams of $12\%$ solution.

28.

Thanh invested a total of ${\$8{,}000}$ in two accounts. One account pays $3\%$ interest annually; the other pays $6\%$ interest annually. At the end of the year, Thanh earned a total of ${\$420}$ in interest. How much money did Thanh invest in each account?

Thanh invested in the $3\%$ account and in the $6\%$ account.

29.

Jerry invested a total of ${\$70{,}000}$ in two accounts. One account pays $7.2\%$ interest annually; the other pays $6.2\%$ interest annually. At the end of the year, Jerry earned a total interest of ${\$4{,}670}\text{.}$ How much money did Jerry invest in each account?

Jerry invested in the $7.2\%$ account and in the $6.2\%$ account.

30.

Carly invested a total of ${\$9{,}000}$ in two accounts. One account pays $5\%$ interest annually; the other pays $4\%$ interest annually. At the end of the year, Carly earned the same amount of interest from both accounts. How much money did Carly invest in each account?

Carly invested in the $5\%$ account and in the $4\%$ account.

31.

Emily invested a total of ${\$83{,}000}$ in two accounts. One account pays ${2.3}\%$ interest annually; the other pays ${7.7}\%$ interest annually. At the end of the year, Emily earned the same amount of interest from both accounts. How much money did Emily invest in each account?

Emily invested in the ${2.3}\%$ account in the ${7.7}\%$ account.

32.

Rebecca invested a total of ${\$10{,}000}$ in two accounts. After a year, one account had earned $13.4\%\text{,}$ while the other account had lost $5.2\%\text{.}$ In total, Rebecca had a net gain of ${\$1{,}247}\text{.}$ How much money did Rebecca invest in each account?

Rebecca invested in the account that grew by $13.4\%$ and in the account that fell by $5.2\%\text{.}$

33.

Gustav invested a total of ${\$5{,}500}$ in two accounts. One account pays $5\%$ interest annually; the other pays $6\%$ interest annually. At the end of the year, Gustav earned a total of ${\$290}$ in interest. Write and solve a system of equations to find how much money Gustav invested in each account.

Gustav invested in the $5\%$ account and in the $6\%$ account.

Some of this section is adapted from Solve Applications with Systems of Equations¹ and Solve Mixture Applications with Systems of Equations² by Wendy Lightheart, OpenStax CNX, which is licensed under CC BY 4.0³

https://cnx.org/contents/8xG8nd5x@1.1:a81syPh0@1/Solve-Applications-with-Systems-of-Equations

https://cnx.org/contents/8xG8nd5x@1.1:jjvYxwLr@1/Solve-Mixture-Applications-with-Systems-of-Equations

http://creativecommons.org/licenses/by/4.0