ORCCA Graphs and Vertex Form

Section 11.1 Graphs and Vertex Form

In this section, we will explore quadratic functions and, in particular, their vertex and factored forms.

Example 11.1.1.

Maia has a remote-controlled airplane and she is going to do a stunt dive where the plane dives toward the ground and back up along a parabolic path. The altitude or height of the plane is given by the function \(H\) where \(H(t)=0.7t^2-23t+200\text{,}\) for \(0 \le t \le 30\text{.}\) The height is measured in feet and the time, \(t\text{,}\) is measured in seconds since the stunt began.

Determine the starting height of the plane as the dive begins.
Determine the height of the plane after \(5\) seconds.
Will the plane hit the ground, and if so, at what time?
If the plane does not hit the ground, what is the closest it gets to the ground, and at what time?
At what time(s) will the plane have an altitude of \(50\) feet?
State the domain and the range of the function (in context).

Explanation

We have graphed the function (see Figure 11.1.2) and we will find the key information and put it in context.

The starting altitude can be read from the vertical intercept, which is \((0,200)\text{.}\) When the stunt begins, the plane has a altitude of \(200\) feet.
When \(t=5\text{,}\) the \(y\)-value is \(102.5\text{.}\) So \(H(5)=102.5\text{.}\) This means that after \(5\) seconds, the plane is \(102.5\) feet above the ground.
From the graph we can see that the parabola does not touch or cross the \(x\)-axis, which represents the ground. This means the plane does not hit the ground and there are no real solutions to the equation \(H(t)=0\text{.}\)

Figure 11.1.2. Graph of \(H(t)=0.7t^2-23t+200\)
The lowest point is the vertex, which is approximately \((16.43, 11.07)\text{.}\) The minimum altitude of the plane is about \(11\) feet, which occurs after about \(16.4\) seconds.
We graph the horizontal line \(y=50\) and look for the points of intersection. The plane will be \(50\) feet above the ground about \(9\) seconds after the plane begins the stunt, and again at about \(24\) seconds.
The domain for this function is given in the problem statement because only part of the parabola represents the path of the plane. The domain is \([0,30]\text{.}\) For the range we look at the possible altitudes of the plane and see that it is \([11.07\ldots,200]\text{.}\) The plane is doing this stunt from \(0\) to \(30\) seconds and its height ranges from about \(11\) to \(200\) feet above the ground.

Subsection 11.1.1 The Vertex Form of a Parabola

We have learned the standard form of a quadratic function's formula, which is \(f(x)=ax^2+bx+c\text{.}\) In this subsection, we will learn another form called the vertex form.

Consider the graphs of \(f(x)=x^2-6x+7\) and \(g(x)=(x-3)^2-2\) on the same axes, shown in Figure 11.1.3.

We see only one parabola because these are two different forms of the same function. Indeed, if we convert \(g(x)\) into standard form:

\begin{align*} g(x)\amp=(x-3)^2-2\\ g(x)\amp=x^2-6x+9-2\\ g(x)\amp=x^2-6x+7 \end{align*}

it is clear that \(f\) and \(g\) are the same function.

the graphs of the two parabolas overlap each other completely — Figure 11.1.3. Graph of \(f(x)=x^2-6x+7\) and \(g(x)=(x-3)^2-2\)

The formula given for \(g\) is written in vertex form, which is very useful because it allows us to read the vertex without doing any calculations. The vertex of the parabola is \((3,-2)\text{.}\) We can see those numbers in \(g(x)=(x-3)^2-2\text{.}\) The \(x\)-value is the solution to \((x-3)=0\text{,}\) and the \(y\)-value is the constant added at the end.

Here are the graphs of three more functions with formulas in vertex form. Compare each function with the vertex of its graph.

the graph of a parabola that opens upward and has a vertex at (2,1) — Figure 11.1.4. \(r(x)=(x-2)^2+1\)

the graph of a wide parabola that opens downward and has a vertex at (-1,3) — Figure 11.1.5. \(s(x)=-\frac{1}{4}(x+1)^2+3\)

the graph of a narrow parabola that opens upward and has a vertex at (-3,-3.5) — Figure 11.1.6. \(t(x)=4(x+3)^2-3.5\)

Notice that the \(x\)-coordinate of the vertex has the opposite sign as the value in the function formula. On the other hand, the \(y\)-coordinate of the vertex has the same sign as the value in the function formula. Let's look at an example to understand why. We will evaluate \(r(2)\text{.}\) \(r(\substitute{2})=(\substitute{2}-2)^2+1=1\text{.}\) The \(x\)-value is the solution to \((x-2)=0\text{,}\) which is positive \(2\text{.}\) When we substitute \(\substitute{2}\) for \(x\) we get the value \(y=1\text{.}\) Note that these coordinates create the vertex at \((2,1)\text{.}\) Now we can define the vertex form of a quadratic function.

Fact 11.1.7. Vertex Form of a Quadratic Function.

A quadratic function with the vertex at the point \((h,k)\) is given by \(f(x)=a(x-h)^2+k\text{.}\)

Checkpoint 11.1.8.

Now let's do the reverse. When given the vertex and the value of \(a\text{,}\) we can write the function in vertex form.

Example 11.1.9.

Write a formula for the quadratic function \(f\) with the given vertex and value of \(a\text{.}\)

Vertex \((-2,8)\text{,}\) \(a=1\)
Vertex \((4,-9)\text{,}\) \(a=-4\)
Vertex \((-3,-1)\text{,}\) \(a=2\)
Vertex \((5,12)\text{,}\) \(a=-3\)

Explanation

The vertex form is \(f(x)=(x+2)^2+8\text{.}\)
The vertex form is \(f(x)=-4(x-4)^2-9\text{.}\)
The vertex form is \(f(x)=2(x+3)^2-1\text{.}\)
The vertex form is \(f(x)=-3(x-5)^2+12\text{.}\)

Subsection 11.1.2 The Domain and Range of a Quadratic Function

Once we read the vertex we can also state the domain and range. All quadratic functions have a domain of \((-\infty,\infty)\) because we can put any value into a quadratic function and get a valid output.

The range, however, depends on the \(y\)-value of the vertex and whether the parabola opens upward or downward. When we have a quadratic function in vertex form we can read the range from the formula. Let's look at the graph of \(f\text{,}\) where \(f(x)=2(x-3)^2-5\text{,}\) as an example.

the graph of a parabola that opens upward with a vertex of (3,-5) — Figure 11.1.10. The graph of \(f(x)=2(x-3)^2-5\)

The domain is \((-\infty,\infty)\text{.}\) The graph of \(f\) opens upward (which we know because \(a=2\gt0\)) so the vertex is the minimum point. The \(y\)-value of \(-5\) is the minimum. Therefore, the range is \([-5,\infty)\text{.}\)

Example 11.1.11.

Identify the domain and range of \(g\text{,}\) where \(g(x)=-3(x+1)^2+6\text{.}\)

Explanation

the graph of a parabola that opens downward with a vertex of (-1,6) — Figure 11.1.12. The graph of \(g(x)=-3(x+1)^2+6\)

The domain is \((-\infty,\infty)\text{.}\) The graph of \(g\) opens downward (which we know because \(a=-3\lt0\)) so the vertex is the maximum point. The \(y\)-value of \(6\) is the maximum. Therefore, the range is \((-\infty,6]\text{.}\)

Checkpoint 11.1.13.

Subsection 11.1.3 The Factored Form of a Parabola

There is another form of a quadratic function's formula, called factored form, which we will explore next. Let's consider the two functions \(q(x)=-x^2+3x+4\) and \(s(x)=-(x-4)(x+1)\text{.}\) We will graph \(y=q(x)\) and \(y=s(x)\) on the same axes, as shown in Figure 11.1.14.

These graphs coincide because the functions are actually the same. We can tell by multiplying out the formula for \(g\) to get back to the formula for \(f\text{.}\)

\begin{align*} g(x)\amp=-(x-4)(x+1)\\ g(x)\amp=-(x^2-3x-4)\\ g(x)\amp=-x^2+3x+4 \end{align*}

Now we can see that \(f\) and \(g\) are really the same function.

the graph of two identical parabolas that open downward and overlap each other completely — Figure 11.1.14. Graph of \(q\) and \(s\)

Factored form is very useful because we can read the \(x\)-intercepts directly from the function, which in this case are \((4,0)\) and \((-1,0)\text{.}\) We find these by looking for the values that make the factors equal to \(0\text{,}\) so the \(x\)-values have the opposite signs as are shown in the formula. To demonstrate this, we will find the \(x\)-intercepts by solving \(g(x)=0\text{.}\)

\begin{align*} g(x)\amp=-(x-4)(x+1)\\ \substitute{0}\amp=-(x-4)(x+1) \end{align*}

\begin{align*} x-4\amp=0\amp\text{or}\amp\amp x+1\amp=0\\ x\amp=4\amp\text{or}\amp\amp x\amp=-1 \end{align*}

This shows us that the \(x\)-intercepts are \((4,0)\) and \((-1,0)\text{.}\)

The \(x\)-values of the \(x\)-intercepts are also called zeros or roots. The zeros or roots of the function \(g\) are \(-1\) and \(4\text{.}\)

Fact 11.1.15. Factored Form of a Quadratic Function.

A quadratic function with horizontal intercepts at \((r,0)\) and \((s,0)\) has the formula \(f(x)=a(x-r)(x-s)\text{.}\)

Checkpoint 11.1.16.

Let's summarize the three forms of a quadratic function's formula:

Standard Form: \(f(x)=ax^2+bx+c\text{,}\) with \(y\)-intercept \((0,c)\text{.}\)
Vertex Form: \(f(x)=a(x-h)^2+k\text{,}\) with vertex \((h,k)\text{.}\)
Factored Form: \(f(x)=a(x-r)(x-s)\text{,}\) with \(x\)-intercepts \((r,0)\) and \((s,0)\text{.}\)

Exercises 11.1.4 Exercises

1.

Let \(f(x)={x^{2}-3x-1}\text{.}\) Evaluate the function for several values of \(x\) to make a table of values \(f\text{.}\)

\(x\)	\(f(x)\)

2.

Let \(g(x)={-x^{2}+3x+2}\text{.}\) Evaluate the function for several values of \(x\) to make a table of values \(g\text{.}\)

\(x\)	\(g(x)\)

3.

Let \(h(x)={-x^{2}-2x+3}\text{.}\) Evaluate the function for several values of \(x\) to make a table of values \(h\text{.}\)

\(x\)	\(h(x)\)

4.

Let \(F(x)={2x^{2}+3x-3}\text{.}\) Evaluate the function for several values of \(x\) to make a table of values \(F\text{.}\)

\(x\)	\(F(x)\)

5.

Let \(F(x)={-3x^{2}-4x+3}\text{.}\) Evaluate the function for several values of \(x\) to make a table of values \(F\text{.}\)

\(x\)	\(F(x)\)

6.

Let \(G(x)={3x^{2}-5x+25}\text{.}\) Evaluate the function for several values of \(x\) to make a table of values \(G\text{.}\)

\(x\)	\(G(x)\)

Graphs

7.

Use point plotting to make a graph of \(f\) where \(f(x)=x^2+3x-2\text{.}\)

8.

Use point plotting to make a graph of \(f\) where \(f(x)=x^2-2x-1\text{.}\)

9.

Use point plotting to make a graph of \(f\) where \(f(x)=-x^2+3x+2\text{.}\)

10.

Use point plotting to make a graph of \(f\) where \(f(x)=-x^2+x+2\text{.}\)

11.

Use point plotting to make a graph of \(f\) where \(f(x)=3x^2-6x-5\text{.}\)

12.

Use point plotting to make a graph of \(f\) where \(f(x)=-3x^2-8x+3\text{.}\)

13.

Use point plotting to make a graph of \(f\) where \(f(x)=-3x^2+4x+49\text{.}\)

14.

Use point plotting to make a graph of \(f\) where \(f(x)=2x^2-2x+41\text{.}\)

Quadratic Functions in Vertex Form

15.

Find the vertex of the graph of \(y=6\!\left(x+8\right)^{2}+8\text{.}\)

16.

Find the vertex of the graph of \(y=8\!\left(x-6\right)^{2}-4\text{.}\)

17.

Find the vertex of the graph of \(y=-10\!\left(x+1\right)^{2}+5\text{.}\)

18.

Find the vertex of the graph of \(y=-8\!\left(x+9\right)^{2}-7\text{.}\)

19.

Find the vertex of the graph of \(y=-5.6\!\left(x-4.9\right)^{2}+1.2\text{.}\)

20.

Find the vertex of the graph of \(y=-3.3\!\left(x+2.1\right)^{2}+9.6\text{.}\)

21.

A graph of a function \(f\) is given. Use the graph to write a formula for \(f\) in vertex form. You will need to identify the vertex and also one more point on the graph to find the leading coefficient \(a\text{.}\)

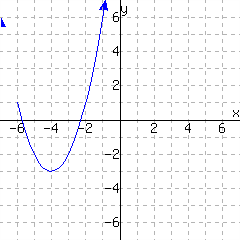
\(\displaystyle{ f(x) =}\)

22.

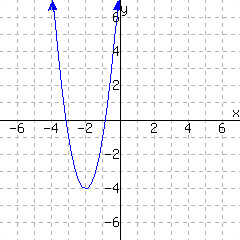
\(\displaystyle{ f(x) =}\)

23.

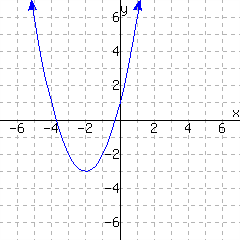
\(\displaystyle{ f(x) =}\)

24.

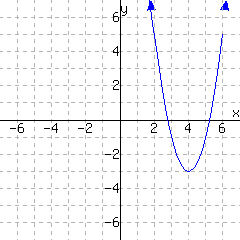
\(\displaystyle{ f(x) =}\)

25.

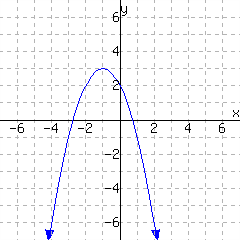
\(\displaystyle{ f(x) =}\)

26.

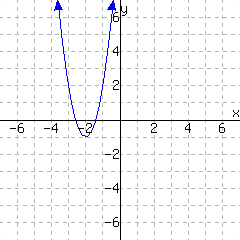
\(\displaystyle{ f(x) =}\)

27.

Write the vertex form for the quadratic function \(f\text{,}\) whose vertex is \((9,8)\) and has leading coefficient \(a=-7\text{.}\)

28.

Write the vertex form for the quadratic function \(f\text{,}\) whose vertex is \((2,-4)\) and has leading coefficient \(a=-5\text{.}\)

29.

Write the vertex form for the quadratic function \(f\text{,}\) whose vertex is \((-4,8)\) and has leading coefficient \(a=-3\text{.}\)

30.

Write the vertex form for the quadratic function \(f\text{,}\) whose vertex is \((8,-7)\) and has leading coefficient \(a=-1\text{.}\)

31.

Let \(F\) be defined by \(F(x)={\left(x-1\right)^{2}+1}\text{.}\)

What is the domain of \(F\text{?}\)
What is the range of \(F\text{?}\)

32.

Let \(G\) be defined by \(G(x)={\left(x+5\right)^{2}+9}\text{.}\)

What is the domain of \(G\text{?}\)
What is the range of \(G\text{?}\)

33.

Let \(H\) be defined by \(H(x)={8.7\!\left(x+2\right)^{2}+6}\text{.}\)

What is the domain of \(H\text{?}\)
What is the range of \(H\text{?}\)

34.

Let \(K\) be defined by \(K(x)={5.3\!\left(x-6\right)^{2}+1}\text{.}\)

What is the domain of \(K\text{?}\)
What is the range of \(K\text{?}\)

35.

Let \(K\) be defined by \(K(x)={-6\!\left(x+5\right)^{2}-4}\text{.}\)

What is the domain of \(K\text{?}\)
What is the range of \(K\text{?}\)

36.

Let \(f\) be defined by \(f(x)={6\!\left(x-3\right)^{2}-9}\text{.}\)

What is the domain of \(f\text{?}\)
What is the range of \(f\text{?}\)

37.

Let \(g\) be defined by \(g(x)={-5\!\left(x-{\frac{1}{2}}\right)^{2} - {\frac{9}{4}}}\text{.}\)

What is the domain of \(g\text{?}\)
What is the range of \(g\text{?}\)

38.

Let \(h\) be defined by \(h(x)={-3\!\left(x + {\frac{1}{8}}\right)^{2}+{\frac{5}{8}}}\text{.}\)

What is the domain of \(h\text{?}\)
What is the range of \(h\text{?}\)

39.

Let \(F\) be defined by \(F(x)={8\!\left(x + {\frac{3}{4}}\right)^{2} - {\frac{9}{7}}}\text{.}\)

What is the domain of \(F\text{?}\)
What is the range of \(F\text{?}\)

40.

Let \(F\) be defined by \(F(x)={-5\!\left(x-1\right)^{2}+{\frac{9}{5}}}\text{.}\)

What is the domain of \(F\text{?}\)
What is the range of \(F\text{?}\)

Three Forms of Quadratic Functions

41.

The quadratic expression \({\left(x-3\right)^{2}-1}\) is written in vertex form.

Write the expression in standard form.
Write the expression in factored form.

42.

The quadratic expression \({\left(x-4\right)^{2}-49}\) is written in vertex form.

Write the expression in standard form.
Write the expression in factored form.

43.

The quadratic expression \({\left(x-4\right)^{2}-9}\) is written in vertex form.

Write the expression in standard form.
Write the expression in factored form.

44.

The quadratic expression \({\left(x-4\right)^{2}-1}\) is written in vertex form.

Write the expression in standard form.
Write the expression in factored form.

Factored Form and Intercepts

45.

The formula for a quadratic function \(h\) is \(h(x)={\left(x+8\right)\!\left(x-4\right)}\text{.}\)

The \(y\)-intercept is .
The \(x\)-intercept(s) is/are .

If there are no \(x\)-intercepts, enter NONE. If there are more than one, use commas to separate the points.

46.

The formula for a quadratic function \(H\) is \(H(x)={\left(x+5\right)\!\left(x+3\right)}\text{.}\)

The \(y\)-intercept is .
The \(x\)-intercept(s) is/are .

If there are no \(x\)-intercepts, enter NONE. If there are more than one, use commas to separate the points.

47.

The formula for a quadratic function \(K\) is \(K(x)={-3\!\left(x+9\right)\!\left(x+5\right)}\text{.}\)

The \(y\)-intercept is .
The \(x\)-intercept(s) is/are .

If there are no \(x\)-intercepts, enter NONE. If there are more than one, use commas to separate the points.

48.

The formula for a quadratic function \(F\) is \(F(x)={-\left(x-3\right)\!\left(x-6\right)}\text{.}\)

The \(y\)-intercept is .
The \(x\)-intercept(s) is/are .

If there are no \(x\)-intercepts, enter NONE. If there are more than one, use commas to separate the points.

49.

The formula for a quadratic function \(f\) is \(f(x)={x\!\left(x+4\right)}\text{.}\)

The \(y\)-intercept is .
The \(x\)-intercept(s) is/are .

If there are no \(x\)-intercepts, enter NONE. If there are more than one, use commas to separate the points.

50.

The formula for a quadratic function \(F\) is \(F(x)={3\!\left(x-9\right)x}\text{.}\)

The \(y\)-intercept is .
The \(x\)-intercept(s) is/are .

If there are no \(x\)-intercepts, enter NONE. If there are more than one, use commas to separate the points.

51.

The formula for a quadratic function \(K\) is \(K(x)={5\!\left(x-2\right)\!\left(x-2\right)}\text{.}\)

The \(y\)-intercept is .
The \(x\)-intercept(s) is/are .

If there are no \(x\)-intercepts, enter NONE. If there are more than one, use commas to separate the points.

52.

The formula for a quadratic function \(h\) is \(h(x)={7\!\left(x+4\right)\!\left(x+4\right)}\text{.}\)

The \(y\)-intercept is .
The \(x\)-intercept(s) is/are .

If there are no \(x\)-intercepts, enter NONE. If there are more than one, use commas to separate the points.

53.

The formula for a quadratic function \(h\) is \(h(x)={9\!\left(2x+7\right)\!\left(9x-1\right)}\text{.}\)

The \(y\)-intercept is .
The \(x\)-intercept(s) is/are .

If there are no \(x\)-intercepts, enter NONE. If there are more than one, use commas to separate the points.

54.

The formula for a quadratic function \(F\) is \(F(x)={-8\!\left(6x+7\right)\!\left(5x+6\right)}\text{.}\)

The \(y\)-intercept is .
The \(x\)-intercept(s) is/are .

If there are no \(x\)-intercepts, enter NONE. If there are more than one, use commas to separate the points.