Section 7.8 Factoring Chapter Review
Subsection 7.8.1 Review of Factoring out the GCF
In Section 7.1 we covered how to factor out the greatest common factor. Recall that the greatest common factor between two expressions is the largest factor that goes in evenly to both expressions.
Example 7.8.1. Finding the Greatest Common Factor.
What is the greatest common factor between \(12x^3y\) and \(42x^2y^2\text{?}\)
Break down each of these into its factors:
Identify the common factors:
\begin{align*} 12x^3y \amp =\attention{2}\cdot 2\cdot \attention{3}\cdot \attention{x}\cdot \attention{x}\cdot x \cdot \attention{y} \amp 42x^2y^2 \amp =\attention{2}\cdot \attention{3}\cdot 7\cdot \attention{x}\cdot \attention{x}\cdot \attention{y} \cdot y \end{align*}With \(2\text{,}\) \(3\text{,}\) two \(x\)'s and a \(y\) in common, the greatest common factor is \(6x^2y\text{.}\)
Example 7.8.2.
What is the greatest common factor between \(18c^3y^2\) and \(27y^3c\text{?}\)
Break down each into factors. You can definitely do this mentally with practice.
And take note of the common factors.
\begin{align*} 18c^3y^2\amp=2\cdot \attention{3}\cdot \attention{3}\cdot \attention{c}\cdot c\cdot c\cdot \attention{y}\cdot \attention{y} \amp 27y^3c\amp= \attention{3}\cdot \attention{3}\cdot 3\cdot \attention{y}\cdot \attention{y}\cdot y\cdot \attention{c} \end{align*}And so the GCF is \(9y^2c\)
Example 7.8.3. Factoring out the Greatest Common Factor.
Factor out the GCF from the expression \(32mn^2-24m^2n-12mn\text{.}\)
To factor out the GCF from the expression \(32mn^2-24m^2n-12mn\text{,}\) first note that the GCF to all three terms is \(4mn\text{.}\) Begin by writing that in front of a blank pair of parentheses and fill in the missing pieces.
Example 7.8.4.
Factor out the GCF from the expression \(14x^3-35x^2\text{.}\)
First, note that the GCF of the terms in \(14x^3-35x^2\) is \(7x^2\text{.}\) Factoring this out, we have:
Example 7.8.5.
Factor out the GCF from the expression \(36m^3n^2-18m^2n^5+24mn^3\text{.}\)
First, note that the GCF of the terms in \(36m^3n^2-18m^2n^5+24mn^3\) is \(6mn^2\text{.}\) Factoring this out, we have:
Example 7.8.6.
Factor out the GCF from the expression \(42f^3w^2-8w^2+9f^3\text{.}\)
First, note that the GCF of the terms in \(42f^3w^2-8w^2+9f^3\) is \(1\text{.}\) The only way to factor the GCF out of this expression is:
Subsection 7.8.2 Review of Factoring by Grouping
In Section 7.2 we covered how to factor by grouping. Recall that factoring using grouping is used on four-term polynomials and also later in the AC method in Section 7.4. Begin by grouping two pairs of terms and factoring out their respective GCF; if all is well, we should be left with two matching pieces in parentheses that can be factored out in their own right.
Example 7.8.7.
Factor the expression \(2x^3+5x^2+6x+15\) using grouping.
Example 7.8.8.
Factor the expression \(2xy-3x-8y+12\) using grouping.
Example 7.8.9.
Factor the expression \(xy-2-2x+y\) using grouping.
This is a special example because if we try to simply follow the algorithm without considering the bigger context, we will fail:
Note that there is no common factor in either grouping, besides \(1\text{,}\) but the groupings themselves don't match. We should now recognize that whatever we are doing isn't working and try something else. It turns out that this polynomial isn't prime; all we need to do is rearrange the polynomial into standard form where the degrees decrease from left to right before grouping.
Example 7.8.10.
Factor the expression \(15m^2-3m-10mn+2n\) using grouping.
Subsection 7.8.3 Review of Factoring Trinomials with Leading Coefficient \(1\)
In Section 7.3 we covered factoring expressions that look like \(x^2+bx+c\text{.}\) The trick was to look for two numbers whose product was \(c\) and whose sum was \(b\text{.}\) Always remember to look for a greatest common factor first, before looking for factor pairs.
Example 7.8.11.
Answer the questions to practice for the factor pairs method.
What two numbers multiply to be \(6\) and add to be \(5\text{?}\)
What two numbers multiply to be \(-6\) and add to be \(5\text{?}\)
What two numbers multiply to be \(-6\) and add to be \(-1\text{?}\)
What two numbers multiply to be \(24\) and add to be \(-10\text{?}\)
What two numbers multiply to be \(-24\) and add to be \(2\text{?}\)
What two numbers multiply to be \(-24\) and add to be \(-5\text{?}\)
What two numbers multiply to be \(420\) and add to be \(44\text{?}\)
What two numbers multiply to be \(-420\) and add to be \(-23\text{?}\)
What two numbers multiply to be \(420\) and add to be \(-41\text{?}\)
What two numbers multiply to be \(6\) and add to be \(5\text{?}\) The numbers are \(2\) and \(3\text{.}\)
What two numbers multiply to be \(-6\) and add to be \(5\text{?}\) The numbers are \(6\) and \(-1\text{.}\)
What two numbers multiply to be \(-6\) and add to be \(-1\text{?}\) The numbers are \(-3\) and \(2\text{.}\)
What two numbers multiply to be \(24\) and add to be \(-10\text{?}\) The numbers are \(-6\) and \(-4\text{.}\)
What two numbers multiply to be \(-24\) and add to be \(2\text{?}\) The numbers are \(6\) and \(-4\text{.}\)
What two numbers multiply to be \(-24\) and add to be \(-5\text{?}\) The numbers are \(-8\) and \(3\text{.}\)
What two numbers multiply to be \(420\) and add to be \(44\text{?}\) The numbers are \(30\) and \(14\text{.}\)
What two numbers multiply to be \(-420\) and add to be \(-23\text{?}\) The numbers are \(-35\) and \(12\text{.}\)
What two numbers multiply to be \(420\) and add to be \(-41\text{?}\) The numbers are \(-20\) and \(-21\text{.}\)
Note that for parts g–i, the factors of 420 are important. Below is a table of factors of 420, which will make it much clearer how the answers were found. To generate a table like this, we start with \(1\) and we work our way up the factors of 420.
| Factor Pair |
| \(1\cdot420\) |
| \(2\cdot210\) |
| \(3\cdot140\) |
| \(4\cdot105\) |
| Factor Pair |
| \(5\cdot84\) |
| \(6\cdot70\) |
| \(7\cdot60\) |
| \(10\cdot42\) |
| Factor Pair |
| \(12\cdot35\) |
| \(14\cdot30\) |
| \(15\cdot28\) |
| \(20\cdot21\) |
It is now much easier to see how to find the numbers in question. For example, to find two numbers that multiply to be \(-420\) and add to be \(-23\text{,}\) simply look in the table for two factors that are \(23\) apart and assign a negative sign appropriately. As we found earlier, the numbers that are \(23\) apart are \(12\) and \(35\text{,}\) and making the larger one negative, we have our answer: \(12\) and \(-35\text{.}\)
Example 7.8.12.
Factor the expression \(x^2-3x-28\)
To factor the expression \(x^2-3x-28\text{,}\) think of two numbers that multiply to be \(-28\) and add to be \(-3\text{.}\) In the Section 7.3, we created a table of all possibilities of factors, like the one shown, to be sure that we never missed the right numbers; however, we encourage you to try this mentally for most problems.
| Factor Pair | Sum of the Pair |
| \(-1\cdot28\) | \(27\) |
| \(-2\cdot14\) | \(12\) |
| \(-4\cdot7\) | \(3\) (close; wrong sign) |
| Factor Pair | Sum of the Pair |
| \(1\cdot(-28)\) | \(-27\) |
| \(2\cdot(-14)\) | \(-12\) |
| \(4\cdot(-7)\) | \(-3\) (what we wanted) |
Since the two numbers in question are \(4\) and \(-7\) that means simply that
Remember that you can always multiply out your factored expression to verify that you have the correct answer. We will use the FOIL expansion.
Example 7.8.13. Factoring in Stages.
Completely factor the expression \(4x^3-4x^2-120x\text{.}\)
Remember that some expressions require more than one step to completely factor. To factor \(4x^3-4x^2-120x\text{,}\) first, always look for any GCF; after that is done, consider other options. Since the GCF is \(4x\text{,}\) we have that
Now the factor inside parentheses might factor further. The key here is to consider what two numbers multiply to be \(-30\) and add to be \(-1\text{.}\) In this case, the answer is \(-6\) and \(5\text{.}\) So, to completely write the factorization, we have:
Example 7.8.14. Factoring Expressions with Higher Powers.
Completely factor the expression \(p^{10}-6p^5-72\text{.}\)
If we have a trinomial with an even exponent on the leading term and the middle term has an exponent that is half the leading term exponent, we can still use the factor pairs method. To factor \(p^{10}-6p^5-72\text{,}\) we note that the middle term exponent \(5\) is half of the leading term exponent \(10\text{,}\) and that two numbers that multiply to be \(-72\) and add to be \(-6\) are \(-12\) and \(6\text{.}\) So the factorization of the expression is
Example 7.8.15. Factoring Expressions with Two Variables.
Completely factor the expression \(x^2-3xy-70y^2\text{.}\)
If an expression has two variables, like \(x^2-3xy-70y^2\text{,}\) we pretend for a moment that the expression is \(x^2-3x-70\text{.}\) To factor this expression we ask ourselves “what two numbers multiply to be \(-70\) and add to be \(-3\text{?}\)” The two numbers in question are \(7\) and \(-10\text{.}\) So \(x^2-3x-70\) factors as \((x+7)(x-10)\text{.}\)
To go back to the original problem now, simply make the two numbers \(7y\) and \(-10y\text{.}\) So, the full factorization is
With problems like this, it is important to verify your answer to be sure that all of the variables ended up where they were supposed to. So, to verify, simply FOIL your answer.
Note that when two or more variables are multiplied together in a term, it is common practice to list the variables in alphabetical order, which is why we rewrote \(7yx\) as \(7xy\text{.}\) This makes it easier to identify like terms.
Example 7.8.16.
Completely factor the expressions.
\(\displaystyle x^2-11x+30\)
\(\displaystyle -s^2+3s+28\)
\(\displaystyle g^2-3g-24\)
\(\displaystyle w^2-wr-30r^2\)
\(\displaystyle z^8+2z^4-63\)
\(\displaystyle x^2-11x+30=(x-6)(x-5)\)
\(\displaystyle -s^2+3s+28=-\left(s^2-3s-28\right)=-(s-7)(s+4)\)
\(g^2-3g-24\) is prime. No two integers multiply to be \(-24\) and add to be \(-3\text{.}\)
\(\displaystyle w^2-wr-30r^2=(w-6r)(w+5r)\)
\(\displaystyle z^8+2z^4-63=\left(z^4-7\right)\left(z^4+9\right)\)
Subsection 7.8.4 Review of Factoring Trinomials with Non-Trivial Leading Coefficient
In Section 7.4 we covered factoring trinomials of the form \(ax^2+bx+c\) when \(a\neq1\) using the AC method.
Example 7.8.17. Using the AC Method.
Completely factor the expression \(9x^2-6x-8\text{.}\)
To factor the expression \(9x^2-6x-8\text{,}\) we first find \(ac\text{:}\)
\(9\cdot(-8)=-72\text{.}\)
-
Examine factor pairs that multiply to \(-72\text{,}\) looking for a pair that sums to \(-6\text{:}\)
Factor Pair Sum of the Pair \(1\cdot-72\) \(-71\) \(2\cdot-36\) \(-34\) \(3\cdot-24\) \(-21\) \(4\cdot-18\) \(-14\) \(6\cdot-12\) \(-6\) \(8\cdot-9\) (no need to go this far) Factor Pair Sum of the Pair \(-1\cdot72\) (no need to go this far) \(-2\cdot36\) (no need to go this far) \(-3\cdot24\) (no need to go this far) \(-4\cdot18\) (no need to go this far) \(-6\cdot12\) (no need to go this far) \(-8\cdot9\) (no need to go this far) -
Intentionally break up the \(-6\) as \(6+(-12)\) and then factor using grouping:
\begin{align*} 9x^2\overbrace{{}-6x}-8\amp=9x^2\overbrace{{}+6x-12x}-8\\ \amp=\left(9x^2+6x\right)+(-12x-8)\\ \amp=3x\highlight{(3x+2)}-4\highlight{(3x+2)}\\ \amp=\highlight{(3x+2)}(3x-4) \end{align*}
Example 7.8.18.
Completely factor the expression \(3x^2+5x-6\text{.}\)
First, note that there is no GCF besides \(1\) and that \(ac=-18\text{.}\) To look for two factors of \(-18\) that add up to \(5\text{,}\) we will make a factor pair table.
| Factor Pair | Sum of the Pair |
| \(1\cdot-18\) | \(-17\) |
| \(2\cdot-9\) | \(-7\) |
| \(3\cdot-6\) | \(-3\) |
| Factor Pair | Sum of the Pair |
| \(-1\cdot18\) | \(17\) |
| \(-2\cdot9\) | \(7\) |
| \(-3\cdot6\) | \(3\) |
Since none of the factor pairs of \(-18\) sum to \(5\text{,}\) we must conclude that this trinomial is prime.
Example 7.8.19.
Completely factor the expression \(3y^2+20y-63\text{.}\)
First, note that \(ac=-189\text{.}\) Looking for two factors of \(-189\) that add up to \(20\text{,}\) we find \(27\) and \(-7\text{.}\) Breaking up the \(+20\) into \(+27-7\text{,}\) we can factor using grouping.
Example 7.8.20. Factoring in Stages with the AC Method.
Completely factor the expression \(8y^3+54y^2+36y\text{.}\)
Recall that some trinomials need to be factored in stages: the first stage is always to factor out the GCF. To factor \(8y^3+54y^2+36y\text{,}\) first note that the GCF of the three terms in the expression is \(2y\text{.}\) Then apply the AC method:
Now we find \(ac=4\cdot18=72\text{.}\) What two factors of \(72\) add up to 27? After checking a few numbers, we find that \(3\) and \(24\) fit the requirements. So:
\begin{align*} \phantom{8y^3+54y^2+36y}\amp=2y\left(4y^2\overbrace{+27y}+18\right)\\ \amp=2y\left(4y^2\overbrace{+3y+24y}+18\right)\\ \amp=2y\left(\left(4y^2+3y\right)+\left(24y+18\right)\right)\\ \amp=2y\left(y\highlight{\left(4y+3\right)}+6\highlight{\left(4y+3\right)}\right)\\ \amp=2y\highlight{\left(4y+3\right)}\left(y+6\right) \end{align*}Example 7.8.21.
Completely factor the expression \(18x^3+26x^2+8x\text{.}\)
First, note that there is a GCF of \(2x\text{,}\) which should be factored out first. Doing this leaves us with \(18x^3+26x^2+8x=2x\left(9x^2+13x+4\right)\text{.}\) Now we apply the AC method on the factor in the parentheses. So, \(ac=36\) and we must find two factors of \(36\) that sum to be \(13\text{.}\) These two factors are \(9\) and \(4\text{.}\) Now we can use grouping.
Subsection 7.8.5 Review of Factoring Special Forms
In Section 7.5 we covered how to factor binomials and trinomials using formulas. Using these formulas, when appropriate, often drastically increased the speed of factoring. Below is a summary of the formulas covered. For each, consider that \(A\) and \(B\) could be any algebraic expressions.
- Difference of Squares
- Perfect Square Sum
- Perfect Square Difference
- Difference of Cubes
- Sum of Cubes
Example 7.8.22. Factoring the Form \(A^2-2AB+B^2\).
Completely factor the expression \(16y^2-24y+9\text{.}\)
To factor \(16y^2-24y+9\) we notice that the expression might be of the form \(A^2-2AB+B^2\text{.}\) To find \(A\) and \(B\text{,}\) we mentally find what needs to be squared to obtain both the first and last terms of the original expression. We determine that \(A=4y\) since \((4y)^2=4^2y^2=16y^2\) and \(B=3\) since \(3^2=9\) . Recall that we now need to check that the \(24y\) matches our \(2AB\text{.}\) Using our values for \(A\) and \(B\text{,}\) we indeed see that \(2AB=-2(4y)(3)=24y\text{.}\) So, we conclude that
Example 7.8.23. Mixed Special Forms Factoring.
Completely factor the expression \(v^3-27\text{.}\)
Completely factor the expression \(9w^2+12w+4\text{.}\)
Completely factor the expression \(4q^2-81\text{.}\)
Completely factor the expression \(9p^2+25\text{.}\)
Completely factor the expression \(121b^2-36\text{.}\)
Completely factor the expression \(25u^2-70u+49\text{.}\)
Completely factor the expression \(64q^3-27y^3\text{.}\)
The first step for each problem is to try to fit the expression to one of the special factoring forms.
-
To factor \(v^3-27\) we notice that the expression is of the form \(A^3-B^3\text{.}\) To find values for \(A\) and \(B\text{,}\) mentally determine what needs to be cubed to obtain the first and last terms. So, \(A=v\) and \(B=3\text{,}\) and using the form \(A^3-B^3=(A-B)(A^2+AB+B^2)\text{,}\) we have that
\begin{align*} v^3-27\amp=(v-3)\left(v^2+(v)(3)+3^2\right)\\ \amp=(v-3)\left(v^2+3v+9\right) \end{align*} -
To factor \(9w^2+12w+4\) we notice that the expression might be of the form \(A^2+2AB+B^2\) where \(A=3w\) and \(B=2\text{.}\) With this formula we need to check the value of \(2AB\text{,}\) which in this case is \(2AB=2(3w)(2)=12w\text{.}\) Since the value of \(2AB\) is correct, the expression must factor as
\begin{equation*} 9w^2+12w+4=(3w+2)^2 \end{equation*} -
To factor \(4q^2-81\) we notice that the expression is of the form \(A^2-B^2\) where \(A=2q\) and \(B=9\text{.}\) Thus, the expression must factor as
\begin{equation*} 4q^2-81=(2q-9)(2q+9) \end{equation*} To factor \(9p^2+25\) we notice that the expression is of the form \(A^2+B^2\text{.}\) This is called a sum of squares. If you recall from the section, the sum of squares is always prime. So \(9p^2+25\) is prime.
-
To completely factor the expression \(121b^2-36\) first note that the expression is of the form \(A^2-B^2\) where \(A=11b\) and \(B=6\text{.}\) So, the expression factors as
\begin{equation*} 121b^2-36=(11b+6)(11b-6)\text{.} \end{equation*} -
To completely factor the expression \(25u^2-70u+49\) first note that the expression might be of the form \(A^2-2AB+B^2\) where \(A=5u\) and \(B=7\text{.}\) Now, we check that \(2AB\) matches the middle term: \(2AB=2(5u)(7)=70u\text{.}\) So, the expression factors as
\begin{equation*} 25u^2-70u+49=(5u-7)^2\text{.} \end{equation*} -
To completely factor the expression \(64q^3-27y^3\) first note that the expression is of the form \(A^3-B^3\) where \(A=4q\) and \(B=3y\text{.}\) So, the expression factors as
\begin{align*} 64q^3-27y^3\amp=(4q-3y)\left((4q)^2+(4q)(3y)+(3y)^2\right)\\ \amp=(4q-3y)\left(16q^2+12qy+9y^2\right) \end{align*}
Subsection 7.8.6 Review of Factoring Strategies
In Section 7.6 we covered a factoring decision tree to help us decide what methods to try when factoring a given expression. Remember to always factor out the GCF first.
Example 7.8.24.
Factor the expressions using an effective method.
\(24xy-20x-18y+15\text{.}\)
\(12t^2+36t+27\text{.}\)
\(8u^2+14u-9\text{.}\)
\(18c^2-98p^2\text{.}\)
-
To factor the expression \(24xy-20x-18y+15\text{,}\) we first look for a GCF. Since the GCF is \(1\text{,}\) we can move further on the flowchart. Since this is a four-term polynomial, we will try grouping.
\begin{align*} 24xy-20x-18y+15\amp=24xy+(-20x)+(-18y)+15\\ \amp=(24xy-20x)+(-18y+15)\\ \amp=4x\highlight{\overbrace{(6x-5)}}-3\highlight{\overbrace{(6x-5)}}\\ \amp=\highlight{(6x-5)}(4x-3) \end{align*} -
To factor the expression \(12t^2+36t+27\text{,}\) we first look for a GCF. Since the GCF is \(\highlight{3}\text{,}\) first we will factor that out.
\begin{align*} 12t^2+36t+27\amp=\highlight{3}\left(4t^2+12t+9\right)\\ \end{align*}Next, we can note that the first and last terms are perfect squares where \(A^2=4t^2\) and \(B=9\text{;}\) so \(A=2t\) and \(B=3\text{.}\) To check the middle term, \(2AB=12t\text{.}\) So the expression factors as a perfect square.
\begin{align*} 12t^2+36t+27\amp=\highlight{3}\left(4t^2+12t+9\right)\\ \amp=\highlight{3}(2t+3)^2 \end{align*} -
To factor the expression \(8u^2+14u-9\text{,}\) we first look for a GCF. Since the GCF is \(1\text{,}\) we can move further on the flowchart. Since the expression is a trinomial with leading coefficient other than \(1\text{,}\) we should try the AC method. Note that \(AC=-72\) and factor pairs of \(-72\) that add up to \(14\) are \(\highlight{18}\) and \(\highlight{-4}\text{.}\)
\begin{align*} 8u^2+\lighthigh{14u}-9\amp=8u^2+\lighthigh{18u-4u}-9\\ \amp=\left(8u^2+18\right)+(-4u-9)\\ \amp=2u\highlight{(4u+9)}-1\highlight{(4u+9)}\\ \amp=\highlight{(4u+9)}(2u-1) \end{align*} -
To factor the expression \(18c^2-98p^2\text{,}\) we first look for a GCF. Since the GCF is \(\highlight{2}\text{,}\) first we will factor that out.
\begin{align*} 18c^2-98p^2\amp=\highlight{2}\left(9c^2-49p^2\right)\\ \end{align*}Now we notice that we have a binomial where both the first and second terms can be written as squares: \(9c^2=(3c)^2\) and \(49p^2=(7p)^2\text{.}\)
\begin{align*} 18c^2-98p^2\amp=\highlight{2}\left(9c^2-49p^2\right)\\ \amp=\highlight{2}(3c-7p)(3c+7p) \end{align*}
Subsection 7.8.7 Solving Quadratic Equations by Factoring
In Section 7.7 we covered the zero product property and learned an algorithm for solving quadratic equations by factoring.
Example 7.8.25. Solving Using Factoring.
Solve the quadratic equations using factoring.
\(\displaystyle x^2-2x-15=0\)
\(\displaystyle 4x^2-40x=-96\)
\(\displaystyle 6x^2+x-12=0\)
\(\displaystyle (x-3)(x+2)=14\)
\(\displaystyle x^3-64x=0\)
-
Use factor pairs.
\begin{align*} x^2-2x-15\amp=0\\ (x-5)(x+3)\amp=0 \end{align*}\begin{align*} x-5\amp=0 \amp\text{ or }\amp\amp x+3\amp=0\\ x\amp=5 \amp\text{ or }\amp\amp x\amp=-3 \end{align*}So the solution set is \(\{5,-3\}\text{.}\)
-
Start by putting the equation in standard form and factoring out the greatest common factor.
\begin{align*} 4x^2-40x\amp=-96\\ 4x^2-40x+96\amp=0\\ 4\left(x^2-10x+24\right)\amp=0\\ 4(x-6)(x-4)\amp=0 \end{align*}\begin{align*} x-6\amp=0 \amp\text{ or }\amp\amp x-4\amp=0\\ x\amp=6 \amp\text{ or }\amp\amp x\amp=4 \end{align*}So the solution set is \(\{4,6\}\text{.}\)
-
Use the AC method.
\begin{align*} 6x^2+x-12\amp=0\\ \end{align*}Note that \(a\cdot c=-72\) and that \(\highlight{9\cdot-8}=-72\) and \(\highlight{9-8}=1\)
\begin{align*} 6x^2\substitute{+9x-8x}-12\amp=0\\ \left(6x^2+9x\right)+\left(-8x-12\right)\amp=0\\ \highlight{3x}\left(2x+3\right)\mathbin{\highlight{-4}}\left(2x+3\right)\amp=0\\ \left(2x+3\right)\highlight{\left(3x-4\right)}\amp=0 \end{align*}\begin{align*} 2x+3\amp=0 \amp\text{ or }\amp\amp \highlight{3x-4}\amp=0\\ x\amp=-\frac{3}{2} \amp\text{ or }\amp\amp x\amp=\highlight{\frac{4}{3}} \end{align*}So the solution set is \(\left\{-\frac{3}{2},\frac{4}{3}\right\}\text{.}\)
-
Start by putting the equation in standard form.
\begin{align*} (x-3)(x+2)\amp=14\\ x^2-x-6\amp=14\\ x^2-x-20\amp=0\\ (x-5)(x+4)\amp=0 \end{align*}\begin{align*} x-5\amp=0 \amp\text{ or }\amp\amp x+4\amp=0\\ x\amp=5 \amp\text{ or }\amp\amp x\amp=-4 \end{align*}So the solution set is \(\{5,-4\}\text{.}\)
-
Even though this equation has a power higher than \(2\text{,}\) we can still find all of its solutions by following the algorithm. Start by factoring out the greatest common factor.
\begin{align*} x^3-64x\amp=0\\ x\left(x^2-64\right)\amp=0\\ x(x-8)(x+8)\amp=0 \end{align*}\begin{align*} x\amp=0 \amp\text{ or }\amp\amp x-8\amp=0 \amp\text{ or }\amp\amp x+8\amp=0\\ x\amp=0 \amp\text{ or }\amp\amp x\amp=8 \amp\text{ or }\amp\amp x\amp=-8 \end{align*}So the solution set is \(\{0,8,-8\}\text{.}\)
Exercises 7.8.8 Exercises
1.
Find the greatest common factor of the following terms.
\({9y}\) and \({54y^{2}}\)
2.
Find the greatest common factor of the following terms.
\({6y}\) and \({30y^{2}}\)
3.
Find the greatest common factor of the following terms.
\({3r^{17}}\) and \({-9r^{10}}\)
4.
Find the greatest common factor of the following terms.
\({9r^{11}}\) and \({-45r^{9}}\)
5.
Find the greatest common factor of the following terms.
\({4x^{12}y^{7}}\text{,}\) \({-32x^{9}y^{12}}\text{,}\) \({8x^{6}y^{17}}\)
6.
Find the greatest common factor of the following terms.
\({2x^{11}y^{8}}\text{,}\) \({-8x^{9}y^{9}}\text{,}\) \({12x^{8}y^{19}}\)
Greatest Common Factor
7.
Factor the given polynomial.
\(8t-8=\)
8.
Factor the given polynomial.
\(5x-5=\)
9.
Factor the given polynomial.
\(2x - 6=\)
10.
Factor the given polynomial.
\(8y+56=\)
11.
Factor the given polynomial.
\({12y^{2}-8y+12}=\)
12.
Factor the given polynomial.
\({90r^{2}+45r+9}=\)
13.
Factor the given polynomial.
\(21r^2 - 26=\)
14.
Factor the given polynomial.
\(11r^2+9=\)
15.
Factor the given polynomial.
\({t\!\left(t+10\right)-7\!\left(t+10\right)}=\)
16.
Factor the given polynomial.
\({t\!\left(t-7\right)-4\!\left(t-7\right)}=\)
17.
Factor the given polynomial.
\({2x\!\left(x+y\right)-3\!\left(x+y\right)}=\)
18.
Factor the given polynomial.
\({3x\!\left(x+y\right)+10\!\left(x+y\right)}=\)
Factor by Grouping
19.
Factor the given polynomial.
\({y^{2}-7y-6y+42}=\)
20.
Factor the given polynomial.
\({y^{2}+4y+3y+12}=\)
21.
Factor the given polynomial.
\({y^{3}-10y^{2}-3y+30}=\)
22.
Factor the given polynomial.
\({r^{3}+6r^{2}+7r+42}=\)
23.
Factor the given polynomial.
\({xy-8x-2y+16}=\)
24.
Factor the given polynomial.
\({xy+9x-5y-45}=\)
25.
Factor the given polynomial.
\({10x^{2}+70xy+3xy+21y^{2}}=\)
26.
Factor the given polynomial.
\({2x^{2}+16xy+7xy+56y^{2}}=\)
One-variable Polynomials
27.
Factor the given polynomial.
\({x^{2}+15x+56}=\)
28.
Factor the given polynomial.
\({y^{2}+6y+5}=\)
29.
Factor the given polynomial.
\({y^{2}-6y-7}=\)
30.
Factor the given polynomial.
\({y^{2}+3y-40}=\)
31.
Factor the given polynomial.
\({r^{2}-9r+20}=\)
32.
Factor the given polynomial.
\({r^{2}-9r+8}=\)
33.
Factor the given polynomial.
\({t^{2}+2t+7}=\)
34.
Factor the given polynomial.
\({t^{2}-4t+7}=\)
35.
Factor the given polynomial.
\({x^{2}-2x+1}=\)
36.
Factor the given polynomial.
\({x^{2}-16x+64}=\)
37.
Factor the given polynomial.
\({5y^{2}+5y-10}=\)
38.
Factor the given polynomial.
\({4y^{2}+20y-24}=\)
39.
Factor the given polynomial.
\({2y^{2}-20y+18}=\)
40.
Factor the given polynomial.
\({3r^{2}-9r+6}=\)
41.
Factor the given polynomial.
\({3r^{10}-9r^{9}-30r^{8}}=\)
42.
Factor the given polynomial.
\({2t^{9}-12t^{8}-14t^{7}}=\)
43.
Factor the given polynomial.
\({-t^{2}-6t+27}=\)
44.
Factor the given polynomial.
\({-x^{2}-2x+35}=\)
Multivariable Polynomials
45.
Factor the given polynomial.
\({x^{2}+5xr-14r^{2}}=\)
46.
Factor the given polynomial.
\({y^{2}-2yx-3x^{2}}=\)
47.
Factor the given polynomial.
\({y^{2}-12yt+27t^{2}}=\)
48.
Factor the given polynomial.
\({y^{2}-6yr+8r^{2}}=\)
49.
Factor the given polynomial.
\({2a^{2}b+2ab-24b}=\)
50.
Factor the given polynomial.
\({2a^{2}b+6ab-8b}=\)
51.
Factor the given polynomial.
\({2x^{3}y+14x^{2}y+12xy}=\)
52.
Factor the given polynomial.
\({6x^{3}y+18x^{2}y+12xy}=\)
Non-trivial Leading Coefficient
53.
Factor the given polynomial.
\({2x^{2}-3x-9}=\)
54.
Factor the given polynomial.
\({3x^{2}-14x-24}=\)
55.
Factor the given polynomial.
\({5y^{2}-2y+5}=\)
56.
Factor the given polynomial.
\({3y^{2}+2y+1}=\)
57.
Factor the given polynomial.
\({15y^{2}+28y+12}=\)
58.
Factor the given polynomial.
\({9r^{2}+21r+10}=\)
59.
Factor the given polynomial.
\({12r^{2}-23r+5}=\)
60.
Factor the given polynomial.
\({12t^{2}-19t+5}=\)
61.
Factor the given polynomial.
\({6t^{2}+38t+12}=\)
62.
Factor the given polynomial.
\({30x^{2}+36x+6}=\)
63.
Factor the given polynomial.
\({4x^{2}-10x+6}=\)
64.
Factor the given polynomial.
\({12y^{2}-16y+4}=\)
65.
Factor the given polynomial.
\({8y^{8}-12y^{7}+4y^{6}}=\)
66.
Factor the given polynomial.
\({6y^{9}-22y^{8}+20y^{7}}=\)
67.
Factor the given polynomial.
\({3r^{2}t^{2}+14rt+8}=\)
68.
Factor the given polynomial.
\({5r^{2}t^{2}+12rt+4}=\)
69.
Factor the given polynomial.
\({2t^{2}-13tx+21x^{2}}=\)
70.
Factor the given polynomial.
\({2t^{2}-11tr+14r^{2}}=\)
71.
Factor the given polynomial.
\({8x^{2}-11xy+3y^{2}}=\)
72.
Factor the given polynomial.
\({8x^{2}-25xy+3y^{2}}=\)
73.
Factor the given polynomial.
\({10y^{2}t^{2}+18yt+8}=\)
74.
Factor the given polynomial.
\({10y^{2}x^{2}+22yx+4}=\)
75.
Factor the given polynomial.
\({14y^{2}x^{2}+7yx-21}=\)
76.
Factor the given polynomial.
\({35r^{2}t^{2}+7rt-42}=\)
77.
Factor the given polynomial.
\({6x^{2}+26xy+24y^{2}}=\)
78.
Factor the given polynomial.
\({4x^{2}+18xy+8y^{2}}=\)
Factor Special Forms
79.
Factor the given polynomial.
\({t^{2}-81}=\)
80.
Factor the given polynomial.
\({x^{2}-25}=\)
81.
Factor the given polynomial.
\({x^{2}-9}=\)
82.
Factor the given polynomial.
\({81y^{2}-64}=\)
83.
Factor the given polynomial.
\({1-16y^{2}}=\)
84.
Factor the given polynomial.
\({49-144y^{2}}=\)
85.
Factor the given polynomial.
\({r^{14}-64}=\)
86.
Factor the given polynomial.
\({r^{10}-25}=\)
87.
Factor the given polynomial.
\({x^{14}-100y^{12}}=\)
88.
Factor the given polynomial.
\({x^{12}-144y^{10}}=\)
89.
Factor the given polynomial.
\({16x^{2}-8x+1}=\)
90.
Factor the given polynomial.
\({121x^{2}-22x+1}=\)
91.
Factor the given polynomial.
\({25x^{2}-70xr+49r^{2}}=\)
92.
Factor the given polynomial.
\({4y^{2}-20yx+25x^{2}}=\)
93.
Factor the given polynomial.
\({x^{3}-343y^{3}}=\)
Hint: \(-343=-7^3\text{.}\)
94.
Factor the given polynomial.
\({x^{3}-512y^{3}}=\)
Hint: \(-512=-8^3\text{.}\)
95.
Factor the given polynomial.
\({r^{4}-16}=\)
96.
Factor the given polynomial.
\({81t^{4}-16}=\)
97.
Factor the given polynomial.
\({6t^{3}-6t}=\)
98.
Factor the given polynomial.
\({5x^{3}-20x}=\)
99.
Factor the given polynomial.
\({10x^{4}t^{3}-90x^{2}t}=\)
100.
Factor the given polynomial.
\({10x^{3}y^{3}-10xy}=\)
101.
Factor the given polynomial.
\({7-7y^{2}}=\)
102.
Factor the given polynomial.
\({72-2y^{2}}=\)
103.
Factor the given polynomial.
\({90r^{10}+60r^{9}+10r^{8}}=\)
104.
Factor the given polynomial.
\({36r^{10}+36r^{9}+9r^{8}}=\)
105.
Factor the given polynomial.
\({t^{6}+729t^{3}}=\)
Hint: \(729=9^3\text{.}\)
106.
Factor the given polynomial.
\({t^{9}+125t^{6}}=\)
107.
Factor the given polynomial.
\({x^{2}+144}=\)
108.
Factor the given polynomial.
\({x^{2}+64}=\)
Solve Quadratic Equations by Factoring
109.
Solve the equation.
\((x - 6)(x - 5) = 0\)
110.
Solve the equation.
\({62\!\left(x-3\right)\!\left(19x+3\right)} = 0\)
111.
Solve the equation.
\({x^{2}+11x+30} = 0\)
112.
Solve the equation.
\({x^{2}-x-6} = 0\)
113.
Solve the equation.
\({x^{2}-6x+8} = 0\)
114.
Solve the equation.
\({x^{2}+14x} = {-48}\)
115.
Solve the equation.
\({x^{2}+7x} = {18}\)
116.
Solve the equation.
\({x^{2}-12x} = {-20}\)
117.
Solve the equation.
\({x^{2}} = {8x}\)
118.
Solve the equation.
\({4x^{2}} = {28x}\)
119.
Solve the equation.
\({5x^{2}} = {-6x}\)
120.
Solve the equation.
\({x^{2}-12x+36}=0\)
121.
Solve the equation.
\({x^{2}}={14x-49}\)
122.
Solve the equation.
\({9x^{2}}={-30x-25}\)
123.
Solve the equation.
\({5x^{2}}={-46x-48}\)
124.
Solve the equation.
\({x^{2}-64} = 0\)
125.
Solve the equation.
\({4x^{2}-81}=0\)
126.
Solve the equation.
\({9x^{2}}={25}\)
127.
Solve the equation.
\({x\!\left(x-6\right)} = {7}\)
128.
Solve the equation.
\({x\!\left(3x+34\right)}={-40}\)
129.
Solve the equation.
\({\left(x-4\right)\!\left(x+6\right)} = {-9}\)
130.
Solve the equation.
\({\left(x+1\right)\!\left(3x+2\right)} = {2x^{2}-2}\)
131.
Solve the equation.
\({x\!\left(x+20\right)}={5\!\left(2x-5\right)}\)
132.
Solve the equation.
\({81x^{2}+72x+16}=0\)
133.
Solve the equation.
\({\left(x+8\right)\!\left(x^{2}+19x+90\right)} = 0\)
134.
Solve the equation.
\({x\!\left(x^{2}-1\right)} = 0\)
135.
Solve the equation.
\({x^{3}-13x^{2}+40x} = 0\)
Application Problems
For the following application problems, write and then solve, by factoring, a quadratic equation, to answer the question.
136.
Two numbers’ sum is \(-17\text{,}\) and their product is \(70\text{.}\) Find these two numbers.
These two numbers are .
137.
Two numbers’ sum is \(2\text{,}\) and their product is \(-35\text{.}\) Find these two numbers.
These two numbers are .
138.
A rectangle’s base is \({7\ {\rm cm}}\) longer than its height. The rectangle’s area is \({78\ {\rm cm^{2}}}\text{.}\) Find this rectangle’s dimensions.
The rectangle’s height is .
The rectangle’s base is .
139.
A rectangle’s base is \({5\ {\rm cm}}\) longer than its height. The rectangle’s area is \({66\ {\rm cm^{2}}}\text{.}\) Find this rectangle’s dimensions.
The rectangle’s height is .
The rectangle’s base is .
140.
The debris from an explosion can be modeled by the equation \(h=112t-16t^2\text{,}\) where \(h\) represents the height, in feet, of the debris above the ground \(t\) seconds after the explosion. After how many seconds will the debris hit the ground?
seconds
141.
The base of a ladder is \(6\) feet from a wall. The ladder is \(2\) feet longer than the height it reaches on the wall. What is the length of the ladder? (Hint: Draw a picture.)
The ladder is feet long.
142.
There is a rectangular lot in the garden, with \({6\ {\rm ft}}\) in length and \({4\ {\rm ft}}\) in width. You plan to expand the lot by an equal length around its four sides, and make the area of the expanded rectangle \({80\ {\rm ft^{2}}}\text{.}\) How long should you expand the original lot in four directions?
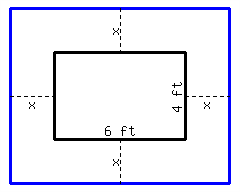
You should expand the original lot by in four directions.
143.
There is a rectangular lot in the garden, with \({9\ {\rm ft}}\) in length and \({7\ {\rm ft}}\) in width. You plan to expand the lot by an equal length around its four sides, and make the area of the expanded rectangle \({143\ {\rm ft^{2}}}\text{.}\) How long should you expand the original lot in four directions?
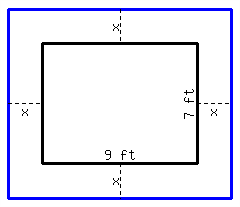
You should expand the original lot by in four directions.
Graphing Quadratic Equations
Graph each curve by algebraically determining its intercepts, vertex, and any other points necessary.
144.
\(y=x^2-6x+8\)
145.
\(y=-x^2+4x\)
146.
\(y=-x^2-10x-25\)
147.
\(y=x^2-36\)
148.
\(y=4x^2-12x+8\)
