Skip to main content

Section 9.3 The Quadratic Formula

We have learned how to solve quadratic equations using factoring and the square root property. In this section, we will learn a third method, the quadratic formula. We will also learn when to use each method and to distinguish between linear and quadratic equations.

Subsection 9.3.1 Solving Quadratic Equations with the Quadratic Formula

The standard form of a quadratic equation is

\begin{equation*} ax^2+bx+c=0 \end{equation*}

Let's look at two examples as a review of solving quadratic equations.

First, let's look at when \(b=0\) and the equation looks like \(ax^2+c=0\text{.}\) One way to solve this type of equation is with the square root property.

Example 9.3.1.

Solve for \(x\) in \(x^2-4=0\text{.}\)

Explanation
\begin{align*} x^2-4\amp=0\\ x^2\amp=4 \end{align*}
\begin{align*} x\amp=-2\amp\text{or}\amp\amp x\amp=2 \end{align*}

The solution set is \(\{-2,2\}\text{.}\)

Second, if we can factor the left side of the equation in \(ax^2+bx+c=0\text{,}\) then we can solve the equation by factoring.

Example 9.3.2.

Solve for \(x\) in \(x^2-4x-12=0\text{.}\)

Explanation
\begin{align*} x^2-4x-12\amp=0\\ (x-6)(x+2)\amp=0 \end{align*}
\begin{align*} x-6\amp=0\amp\text{or}\amp\amp x+2\amp=0\\ x\amp=6\amp\text{or}\amp\amp x\amp=-2 \end{align*}

The solution set is \(\{-2,6\}\text{.}\)

A third method for solving a quadratic equation is to use what is known as the quadratic formula.

As we have seen from solving quadratic equations, there can be at most two solutions. Both of the solutions are included in the quadratic formula with the \(\pm\) symbol. We could write the two solutions separately as

\begin{align*} x=\frac{-b-\sqrt{b^2-4ac}}{2a}\amp\amp\text{ or }\amp\amp x=\frac{-b+\sqrt{b^2-4ac}}{2a}\text{,} \end{align*}

but it is more efficient to simplify them together.

This method for solving quadratic equations will work to solve every quadratic equation. It is most helpful when \(b\ne0\) and when \(ax^2+bx+c\) cannot be factored. In this section, we will only focus on how to use the formula.

In Section 7.7, we saw an example where a physics class launched a tennis ball off the roof of a building. In that example, the numbers were simplified so we could solve it by factoring. Now we will solve a similar example with more realistic numbers.

Example 9.3.4.

Linh is in another physics class that launches a tennis ball from a rooftop that is \(90.2\) feet above the ground. They fire it directly upward at a speed of \(14.4\) feet per second and measure the time it takes for the ball to hit the ground below. We can model the height of the tennis ball, \(h\text{,}\) in feet, with the quadratic equation \(h=-16x^2+14.4x+90.2\text{,}\) where \(x\) represents the time in seconds after the launch. According to the model, when should the ball hit the ground? Round the time to one decimal place.

The ground has a height of \(0\) feet. Substituting \(0\) for \(h\) in the equation, we have this quadratic equation:

\begin{equation*} 0=-16x^2+14.4x+90.2 \end{equation*}

We cannot solve this equation with factoring or the square root property, so we will use the quadratic formula. First, we will identify that \(\highlight{a=-16}\text{,}\) \(\highlight{b=14.4}\) and \(\highlight{c=90.2}\text{,}\) and substitute them into the formula:

\begin{align*} x\amp=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ x\amp=\frac{-(\substitute{14.4})\pm\sqrt{(\substitute{14.4})^2-4(\substitute{-16})(\substitute{90.2})}}{2(\substitute{-16})}\\ x\amp=\frac{-14.4\pm\sqrt{207.36-(-5772.8)}}{-32}\\ x\amp=\frac{-14.4\pm\sqrt{207.36+5772.8}}{-32}\\ x\amp=\frac{-14.4\pm\sqrt{5980.16}}{-32}\\ \end{align*}

These are the exact solutions, but because we have a context we want to approximate the solutions with decimals.

\begin{align*} x\amp\approx-2.0\text{ or }x\approx2.9 \end{align*}

We don't use the negative solution because a negative time does not make sense in this context. The ball will hit the ground approximately \(2.9\) seconds after it is launched.

The quadratic formula can be used to solve any quadratic equation, but it requires that you don't make any slip-up with remembering the formula, that you correctly identify \(a\text{,}\) \(b\text{,}\) and \(c\text{,}\) and that you don't make any arithmetic mistakes when you calculate and simplify. We recommend that you always check whether you can factor or use the square root property before using the quadratic formula. Here is another example.

Example 9.3.5.

Solve for \(x\) in \(2x^2-9x+5=0\text{.}\)

Explanation

First, we check and see that we cannot factor the left side (because we can't find two numbers that multiply to \(10\) and add to \(-9\)) or use the square root property (because \(b\neq0\)) so we must use the quadratic formula. Next we identify that \(\highlight{a=2}\text{,}\) \(\highlight{b=-9}\) and \(\highlight{c=5}\text{.}\) We will substitute them into the quadratic formula:

\begin{align*} x\amp=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ x\amp=\frac{-(\substitute{-9})\pm\sqrt{(\substitute{-9})^2-4(\substitute{2})(\substitute{5})}}{2(\substitute{2})}\\ x\amp=\frac{9\pm\sqrt{81-40}}{4}\\ x\amp=\frac{9\pm\sqrt{41}}{4} \end{align*}

This is fully simplified because we cannot simplify \(\sqrt{41}\) or reduce the fraction. The solution set is \(\left\{\frac{9-\sqrt{41}}{4},\frac{9+\sqrt{41}}{4}\right\}\text{.}\) We do not have a context here so we leave the solutions in their exact form.

When a quadratic equation is not in standard form we must convert it before we can identify the values of \(a\text{,}\) \(b\) and \(c\text{.}\) We will show that in the next example.

Example 9.3.6.

Solve for \(x\) in \(x^2=-10x-3\text{.}\)

Explanation

First, we convert the equation into standard form by adding \(10x\) and \(3\) to each side of the equation:

\begin{equation*} x^2+10x+3=0 \end{equation*}

Next, we check and see that we cannot factor the left side or use the square root property so we must use the quadratic formula. We identify that \(\highlight{a=1}\text{,}\) \(\highlight{b=10}\) and \(\highlight{c=3}\text{.}\) We will substitute them into the quadratic formula:

\begin{align*} x\amp=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ x\amp=\frac{-\substitute{10}\pm\sqrt{(\substitute{10})^2-4(\substitute{1})(\substitute{3})}}{2(\substitute{1})}\\ x\amp=\frac{-10\pm\sqrt{100-12}}{2}\\ x\amp=\frac{-10\pm\sqrt{88}}{2} \end{align*}

Now we need to simplify the square root:

\begin{align*} x\amp=\frac{-10\pm2\sqrt{22}}{2}\\ \end{align*}

Lastly we need to reduce the fractions, which can be done by separating terms:

\begin{align*} x\amp=\frac{-10}{2}\pm\frac{2\sqrt{22}}{2}\\ x\amp=-5\pm\sqrt{22} \end{align*}

The solution set is \(\{-5-\sqrt{22}, -5+\sqrt{22}\}\text{.}\)

Sometimes, it may not be immediately apparent that you will need to solve a quadratic equation when first attempting a problem, as will be demonstrated in the next example.

Example 9.3.7.

Solve \(C(t)=0.35\text{,}\) where \(C(t)=\frac{3t}{t^2+8}\) gives a drug's concentration in milligrams per liter \(t\) hours since an injection. (This function was explored in the introduction of Section 8.2.)

Explanation

To solve \(C(t)=0.35\text{,}\) we'll begin by setting up \(\frac{3t}{t^2+8}=0.35\text{.}\) We'll begin by identifying that the LCD is \(t^2+8\text{,}\) and multiply each side of the equation by this:

\begin{align*} \frac{3t}{t^2+8}\amp=0.35\\ \frac{3t}{\highlight{\cancel{t^2+8}}}\multiplyright{\highlight{\cancel{\left(t^2+8\right)}}}\amp=0.35\multiplyright{\left(t^2+8\right)}\\ 3t\amp=0.35\left(t^2+8\right)\\ 3t\amp=0.35t^2+2.8 \end{align*}

This results in a quadratic equation so we will put it in standard form and use the quadratic formula:

\begin{align*} 0\amp=0.35t^2-3t+2.8\\ t\amp=\frac{-(-3)\pm \sqrt{(-3)^2-4(0.35)(2.8)}}{2(0.35)}\\ t\amp=\frac{3\pm \sqrt{5.08}}{0.7}\\ t\amp\approx 1.066 \text{ or } t\approx 7.506 \end{align*}

Each of these answers should be checked in the original equation; they both work. In context, this means that the drug concentration will reach \(0.35\) milligrams per liter about \(1.066\) hours after the injection was given, and again \(7.506\) hours after the injection was given.

Remark 9.3.8.

The irrational solutions to quadratic equations can be checked, although doing so can sometimes involve a lot of simplification and is not shown throughout this section. As an example, to check the solution of \(-5+\sqrt{22}\) from Example 9.3.6, we would replace \(x\) with \(-5+\sqrt{22}\) and check that the two sides of the equation are equal. This check is shown here:

\begin{align*} x^2\amp=-10x-3\\ (\substitute{-5+\sqrt{22}})^2\amp\stackrel{?}{=}-10(\substitute{-5+\sqrt{22}})-3\\ (-5)^2+2(-5)(\sqrt{22})+(\sqrt{22})^2\amp\stackrel{?}{=}-10(-5+\sqrt{22})-3\\ 25-10\sqrt{22}+22 \amp\stackrel{?}{=}50-10\sqrt{22}-3\\ 47-10\sqrt{22}\amp\stackrel{\checkmark}{=}47-10\sqrt{22} \end{align*}

When the radicand from the quadratic formula (which is called the discriminant ) is a negative number, the quadratic equation has no real solution. Example 9.3.9 shows what happens in this case.

Example 9.3.9.

Solve for \(y\) in \(y^2-4y+8=0\text{.}\)

Explanation

Identify that \(\highlight{a=1}\text{,}\) \(\highlight{b=-4}\) and \(\highlight{c=8}\text{.}\) We will substitute them into the quadratic formula:

\begin{align*} y\amp=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ \amp=\frac{-(\substitute{-4})\pm\sqrt{(\substitute{-4})^2-4(\substitute{1})(\substitute{8})}}{2(\substitute{1})}\\ \amp=\frac{4\pm\sqrt{16-32}}{2}\\ \amp=\frac{4\pm\sqrt{-16}}{2} \end{align*}

The square root of a negative number is not a real number, so we will simply state that this equation has no real solutions.

Subsection 9.3.2 Recognizing Linear and Quadratic Equations

Now that we have solved both linear and quadratic equations, it is important to identify each type of equation. Recall that a linear equation has a degree of one and a quadratic equation has a degree of two. If there is any other operation on the variable such as division or a square root then it is not linear or quadratic. We can have other operations on numbers, but not the variables. Let's look at an example.

Checkpoint 9.3.10.

Identify whether each equation is linear, quadratic or neither.

Subsection 9.3.3 Solving Linear and Quadratic Equations

When an equation is linear, we move all variable terms to one side of the equation and all constant terms to the other side. Then we use division if needed to solve for the variable. This is outlined in List 3.1.3.

When an equation is quadratic, we have three different methods we can use. Here is an outline of the general process for determining which method to use.

Here are some examples:

Example 9.3.12.

Solve for \(x\) in \(x^2=7x^2-12\text{.}\)

Explanation

This is a quadratic equation because there are \(x^2\) terms. There are no \(x\) terms so we will use the square root method. We start by combining the \(x^2\) terms on the left.

\begin{align*} x^2\amp=7x^2-12\\ -6x^2\amp=-12\\ x^2\amp=2 \end{align*}
\begin{align*} x\amp=-\sqrt{2}\amp\text{or}\amp\amp x=\sqrt{2} \end{align*}

The solution set is \(\{-\sqrt{2},\sqrt{2}\}\text{.}\)

Example 9.3.13.

Solve for \(p\) in \(p^2=-2p+2\text{.}\)

Explanation

This is a quadratic equation that also contains a linear term so we will put the equation in standard form. Then we see that the left side does not factor so we will use the quadratic formula.

\begin{align*} p^2+2p-2\amp=0\\ p\amp=\frac{-(2)\pm\sqrt{(2)^2-4(1)(-2)}}{2(1)}\\ p\amp=\frac{-2\pm\sqrt{4+8}}{2}\\ p\amp=\frac{-2\pm\sqrt{12}}{2}\\ p\amp=\frac{-2\pm2\sqrt{3}}{2}\\ p\amp=\frac{-2}{2}\pm\frac{2\sqrt{3}}{2}\\ p\amp=-1\pm \sqrt{3} \end{align*}

The solution set is \(\{-1-\sqrt{3},-1+\sqrt{3}\}\text{.}\)

Example 9.3.14.

Solve for \(t\) in \(7-t=9t+11\text{.}\)

Explanation

This is a linear equation so we will combine the linear terms on one side and the constant terms on the other side.

\begin{align*} -10t\amp=4\\ t\amp=\frac{4}{-10}\\ t\amp=-\frac{2}{5} \end{align*}

The solution set is \(\left\{-\frac{2}{5}\right\}\text{.}\)

Example 9.3.15.

Solve for \(z\) in \(z^2-10=3z+30\text{.}\)

Explanation

This is a quadratic equation with a linear term so we will put it in standard form. Then we see that the left side factors so we solve by factoring.

\begin{align*} z^2-10=3z+30\\ z^2-3z-40\amp=0\\ (z+5)(z-8)\amp=0 \end{align*}
\begin{align*} z+5\amp=0\amp\amp\text{ or }\amp z-8\amp=0\\ z\amp=-5\amp\amp\text{ or }\amp z\amp=8 \end{align*}

The solution set is \(\{-5, 8\}\text{.}\)

Exercises 9.3.4 Exercises

Review and Warmup
1.

Evaluate \(\displaystyle{{\frac{7B+9b-3}{2B+4b}}}\) for \(B=-9\) and \(b=-5\text{.}\)

2.

Evaluate \(\displaystyle{{\frac{-C-8A+8}{3C+9A}}}\) for \(C=8\) and \(A=-9\text{.}\)

3.

Evaluate the expression \(\displaystyle \frac{1}{4} \big( x + 4 \big)^2 - 6\) when \(x = -8\text{.}\)

4.

Evaluate the expression \(\displaystyle \frac{1}{4} \big( x + 4 \big)^2 - 4\) when \(x = -8\text{.}\)

5.

Evaluate the expression \(-16t^{2}+64t+128\) when \(t=-5\text{.}\)

6.

Evaluate the expression \(-16t^{2}+64t+128\) when \(t=-4\text{.}\)

7.

Evaluate the expression \({x^{2}}\text{:}\)

  1. For \(x=3\text{.}\)

  2. For \(x=-6\text{.}\)

8.

Evaluate the expression \({y^{2}}\text{:}\)

  1. For \(y=8\text{.}\)

  2. For \(y=-2\text{.}\)

9.

Evaluate each algebraic expression for the given value(s):

\(\displaystyle\frac{\sqrt{x}}{y}-\frac{y}{x}\text{,}\) for \(x = 36\) and \(y = 5\text{:}\)

10.

Evaluate each algebraic expression for the given value(s):

\(\displaystyle\frac{\sqrt{x}}{y}-\frac{y}{x}\text{,}\) for \(x = 49\) and \(y = -9\text{:}\)

Solve Quadratic Equations Using the Quadratic Formula
11.

Solve the equation.

\({x^{2}-2x-11}= 0\)

12.

Solve the equation.

\({x^{2}-10x+18}= 0\)

13.

Solve the equation.

\({15x^{2}+17x-4}=0\)

14.

Solve the equation.

\({4x^{2}-4x-15}=0\)

15.

Solve the equation.

\({x^{2}}= {-\left(5x+3\right)}\)

16.

Solve the equation.

\({x^{2}}= {9x-19}\)

17.

Solve the equation.

\({x^{2}-9x+9}= 0\)

18.

Solve the equation.

\({x^{2}+7x+1}= 0\)

19.

Solve the equation.

\({2x^{2}-3x-1}= 0\)

20.

Solve the equation.

\({4x^{2}-x-1}= 0\)

21.

Solve the equation.

\({4x^{2}-6x-9}= 0\)

22.

Solve the equation.

\({3x^{2}-4x-8}= 0\)

23.

Solve the equation.

\({5x^{2}+5x+5}= 0\)

24.

Solve the equation.

\({2x^{2}-4x+4}= 0\)

Solve Quadratic Equations Using an Appropriate Method
25.

Solve the equation.

\(4x^2 - 100 = 0\)

26.

Solve the equation.

\(5x^2 - 80 = 0\)

27.

Solve the equation.

\({7c+10} = {c+34}\)

28.

Solve the equation.

\({10A+5} = {A+23}\)

29.

Solve the equation.

\({64x^{2}-49}=0\)

30.

Solve the equation.

\({25x^{2}-36}=0\)

31.

Solve the equation.

\(-1-7t^2 = -6\)

32.

Solve the equation.

\(11-5x^2 = 9\)

33.

Solve the equation.

\(x^2 - 69x= 0\)

34.

Solve the equation.

\(x^2 - 49x= 0\)

35.

Solve the equation.

\({6a+4} = {-2a+4-9a}\)

36.

Solve the equation.

\({3c+8} = {-9c+8-9c}\)

37.

Solve the equation.

\({x^{2}-7x} = {8}\)

38.

Solve the equation.

\({x^{2}-x} = {20}\)

39.

Solve the equation.

\(\left(x+6\right)^2 = 4\)

40.

Solve the equation.

\(\left(x+8\right)^2 = 100\)

41.

Solve the equation.

\({x^{2}}= {x+3}\)

42.

Solve the equation.

\({x^{2}}= {7x-9}\)

43.

Solve the equation.

\({3x^{2}}= {1-x}\)

44.

Solve the equation.

\({4x^{2}}= {-\left(7x+2\right)}\)

45.

Solve the equation.

\(20 - 6 ( y+4 )^2 = -4\)

46.

Solve the equation.

\(36 - 5 ( r+4 )^2 = -9\)

47.

Solve the equation.

\({-34}={-4C-4-C}\)

48.

Solve the equation.

\({-8}={-10m-8-m}\)

Quadratic Formula Applications
49.

Two numbers’ sum is \(15\text{,}\) and their product is \(54\text{.}\) Find these two numbers.

These two numbers are .

50.

Two numbers’ sum is \(3\text{,}\) and their product is \(-70\text{.}\) Find these two numbers.

These two numbers are .

51.

Two numbers’ sum is 2.5, and their product is -68.16. Find these two numbers.

52.

Two numbers’ sum is -8, and their product is 14.04. Find these two numbers.

53.

A rectangle’s base is \({6\ {\rm cm}}\) longer than its height. The rectangle’s area is \({72\ {\rm cm^{2}}}\text{.}\) Find this rectangle’s dimensions.

The rectangle’s height is .

The rectangle’s base is .

54.

A rectangle’s base is \({9\ {\rm cm}}\) longer than its height. The rectangle’s area is \({112\ {\rm cm^{2}}}\text{.}\) Find this rectangle’s dimensions.

The rectangle’s height is .

The rectangle’s base is .

55.

A rectangle’s base is \({5\ {\rm in}}\) shorter than four times its height. The rectangle’s area is \({44\ {\rm in^{2}}}\text{.}\) Find this rectangle’s dimensions.

The rectangle’s height is .

The rectangle’s base is .

56.

A rectangle’s base is \({1\ {\rm in}}\) shorter than twice its height. The rectangle’s area is \({28\ {\rm in^{2}}}\text{.}\) Find this rectangle’s dimensions.

The rectangle’s height is .

The rectangle’s base is .

57.

You will build a rectangular sheep pen next to a river. There is no need to build a fence along the river, so you only need to build three sides.

You have a total of \(570\) feet of fence to use, and the area of the pen must be \(40600\) square feet. Find the dimensions of the pen.

There should be two solutions:

When the width is feet, the length is feet.

When the width is feet, the length is feet.

58.

You will build a rectangular sheep pen next to a river. There is no need to build a fence along the river, so you only need to build three sides.

You have a total of \(550\) feet of fence to use, and the area of the pen must be \(37500\) square feet. Find the dimensions of the pen.

There should be two solutions:

When the width is feet, the length is feet.

When the width is feet, the length is feet.

59.

There is a rectangular lot in the garden, with \({10\ {\rm ft}}\) in length and \({4\ {\rm ft}}\) in width. You plan to expand the lot by an equal length around its four sides, and make the area of the expanded rectangle \({160\ {\rm ft^{2}}}\text{.}\) How long should you expand the original lot in four directions?

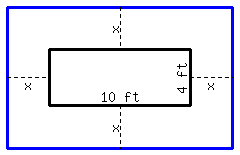
You should expand the original lot by in four directions.

60.

There is a rectangular lot in the garden, with \({5\ {\rm ft}}\) in length and \({3\ {\rm ft}}\) in width. You plan to expand the lot by an equal length around its four sides, and make the area of the expanded rectangle \({99\ {\rm ft^{2}}}\text{.}\) How long should you expand the original lot in four directions?

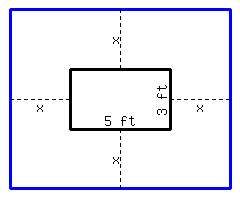
You should expand the original lot by in four directions.

61.

One car started at Town A, and traveled due north at \(45\) miles per hour. \(1\) hours later, another car started at the same spot and traveled due east at \(55\) miles per hour. Assume both cars don’t stop, after how many hours since the second car starts would the distance between them be \(324\) miles? Round your answer to two decimal places if needed.

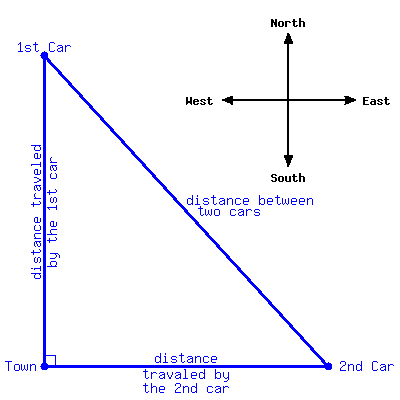
Approximately hours since the second car starts, the distance between those two cars would be \(324\) miles.

62.

One car started at Town A, and traveled due north at \(50\) miles per hour. \(2.5\) hours later, another car started at the same spot and traveled due east at \(40\) miles per hour. Assume both cars don’t stop, after how many hours since the second car starts would the distance between them be \(348\) miles? Round your answer to two decimal places if needed.

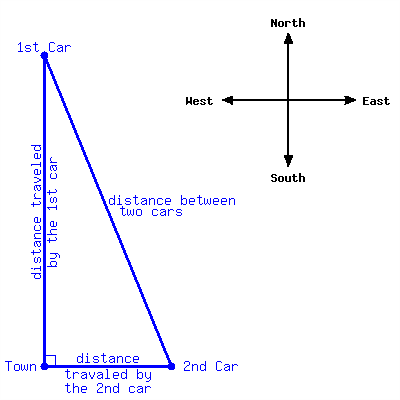
Approximately hours since the second car starts, the distance between those two cars would be \(348\) miles.

63.

An object is launched upward at the height of \(290\) meters. Its height can be modeled by

\begin{equation*} h=-4.9t^2+90t+290\text{,} \end{equation*}

where \(h\) stands for the object’s height in meters, and \(t\) stands for time passed in seconds since its launch. The object’s height will be \(340\) meters twice before it hits the ground. Find how many seconds since the launch would the object’s height be \(340\) meters. Round your answers to two decimal places if needed.

The object’s height would be \(340\) meters the first time at seconds, and then the second time at seconds.

64.

An object is launched upward at the height of \(310\) meters. Its height can be modeled by

\begin{equation*} h=-4.9t^2+70t+310\text{,} \end{equation*}

where \(h\) stands for the object’s height in meters, and \(t\) stands for time passed in seconds since its launch. The object’s height will be \(330\) meters twice before it hits the ground. Find how many seconds since the launch would the object’s height be \(330\) meters. Round your answers to two decimal places if needed.

The object’s height would be \(330\) meters the first time at seconds, and then the second time at seconds.

65.

Currently, an artist can sell \(270\) paintings every year at the price of \({\$50.00}\) per painting. Each time he raises the price per painting by \({\$20.00}\text{,}\) he sells \(20\) fewer paintings every year.

Assume he will raise the price per painting \(x\) times, then he will sell \(270-20x\) paintings every year at the price of \(50+20x\) dollars. His yearly income can be modeled by the equation:

\begin{equation*} i=(50+20x)(270-20x) \end{equation*}

where \(i\) stands for his yearly income in dollars. If the artist wants to earn \({\$20{,}700.00}\) per year from selling paintings, what new price should he set?

To earn \({\$20{,}700.00}\) per year, the artist could sell his paintings at two different prices. The lower price is per painting, and the higher price is per painting.

66.

Currently, an artist can sell \(210\) paintings every year at the price of \({\$120.00}\) per painting. Each time he raises the price per painting by \({\$20.00}\text{,}\) he sells \(10\) fewer paintings every year.

Assume he will raise the price per painting \(x\) times, then he will sell \(210-10x\) paintings every year at the price of \(120+20x\) dollars. His yearly income can be modeled by the equation:

\begin{equation*} i=(120+20x)(210-10x) \end{equation*}

where \(i\) stands for his yearly income in dollars. If the artist wants to earn \({\$28{,}000.00}\) per year from selling paintings, what new price should he set?

To earn \({\$28{,}000.00}\) per year, the artist could sell his paintings at two different prices. The lower price is per painting, and the higher price is per painting.

67.

Solve for \(x\) in the equation \(mx^{2}+nx+p=0\text{.}\)