Section 9.8 Solving Quadratic Equations Chapter Review
Subsection 9.8.1 Square Root Properties
In Section 9.1 we covered the definition of a square root, how to estimate and simplify square roots, multiplication and division properties of square roots, and rationalizing the denominator.
Example 9.8.1. Estimating Square Roots.
Estimate the value of \(\sqrt{28}\) without a calculator.
To estimate \(\sqrt{28}\text{,}\) we can find the nearest perfect squares that are whole numbers on either side of \(28\text{.}\) Recall that the perfect squares are \(1, 4, 9, 16, 25, 36, 49, 64,\dots\) The perfect square that is just below \(28\) is \(25\) and the perfect square just above \(28\) is \(36\text{.}\) This tells us that \(\sqrt{28}\) is between \(\sqrt{25}\) and \(\sqrt{36}\text{,}\) or between \(5\) and \(6\text{.}\) We can also say that \(\sqrt{28}\) is closer to \(5\) than \(6\) because \(28\) is closer to \(25\text{,}\) so we think \(5.2\) or \(5.3\) would be a good estimate.
On the calculator we can see that \(\sqrt{28}\approx5.29\text{,}\) so our guess was very close to reality.
Example 9.8.2. Multiplication and Division Properties of Square Roots.
Simplify the expressions using the multiplication and division properties of square roots.
\(\sqrt{18}\cdot\sqrt{2}\text{.}\)
\(\frac{\sqrt{18}}{\sqrt{2}}\text{.}\)
\(\displaystyle \begin{aligned}[t] \sqrt{18}\cdot\sqrt{2}\amp=\sqrt{18\cdot2}\\ \amp=\sqrt{36}\\ \amp=6\end{aligned} \)
\(\displaystyle \begin{aligned}[t] \frac{\sqrt{18}}{\sqrt{2}}\amp=\sqrt{\frac{18}{2}}\\ \amp=\sqrt{9}\\ \amp=3\end{aligned} \)
Example 9.8.3. Simplifying Square Roots.
Simplify the expression \(\sqrt{54}\text{.}\)
Recall that the perfect squares are \(1, 4, 9, 16, 25, 36, 49, 64,\dots\) To simplify the \(\sqrt{54}\text{,}\) we need to look at that list and find the largest perfect square the goes into \(54\) evenly. In this case, it is \(\highlight{9}\text{.}\) We then break up \(54\) into two factors \(\highlight{9}\) and \(6\text{,}\) and we have:
Since \(6\) has no perfect square factors, we can stop.
Example 9.8.4. Multiplying Square Root Expressions.
Simplify the expression \(\sqrt{50}\cdot\sqrt{27}\text{.}\)
Note that \(25\) is a perfect-square factor of \(50\) and that \(9\) is a perfect-square factor of \(27\text{.}\) Now we have:
Example 9.8.5. Adding and Subtracting Square Root Expressions.
Simplify the expression \(\sqrt{32}+\sqrt{50}\text{.}\)
Recall that radicals can only be added if the radicands match identically, so we cannot initially combine these two terms. However, if we simplify first, we may be able to add terms later. Note that \(16\) is a perfect-square factor of \(32\) and that \(25\) is a perfect-square factor of \(50\text{.}\)
Example 9.8.6. Rationalizing the Denominator.
Rationalize the denominator in the expression \(\frac{2}{\sqrt{6}}\text{.}\)
Example 9.8.7. More Complicated Square Roots.
Expand \(\left(\sqrt{5}+\sqrt{3}\right)^2\text{.}\)
We will use the FOIL method to expand this expression:
Subsection 9.8.2 Solving Quadratic Equations by Using a Square Root
In Section 9.2 we covered how to solve quadratic equations using the square root property and how to use the Pythagorean Theorem.
Example 9.8.8. Solving Quadratic Equations Using the Square Root Property.
Solve for \(w\) in \(3(2-w)^2-24=0\text{.}\)
It's important here to suppress any urge you may have to expand the squared binomial. We begin by isolating the squared expression.
Now that we have the squared expression isolated, we can use the square root property.
The solution set is \(\left\{2\sqrt{2}+2,-2\sqrt{2}+2\right\}\text{.}\)
Example 9.8.9. The Pythagorean Theorem.
Faven was doing some wood working in her garage. She needed to cut a triangular piece of wood for her project that had a hypotenuse of \(16\) inches, and the sides of the triangle should be equal in length. How long should she make her sides?
Let's start by representing the length of the triangle, measured in inches, by the letter \(x\text{.}\) That would also make the other side \(x\) inches long.
Faven should now set up the Pythagorean theorem regarding the picture. That would be
Solving this equation, we have:
Faven should make the sides of her triangle about \(11.3\) inches long to force the hypotenuse to be \(16\) inches long.
Subsection 9.8.3 The Quadratic Formula
In Section 9.3 we covered how to use the quadratic formula to solve any quadratic equation, as well as an Process 9.3.11 to help solve linear and quadratic equations.
Example 9.8.11. Solving Quadratic Equations with the Quadratic Formula.
Solve the equations using the quadratic formula.
\(\displaystyle x^2+4x=6\)
\(\displaystyle 5x^2-2x+1=0\)
-
First we should change the equation into standard form.
\begin{align*} x^2+4x\amp=6\\ x^2+4x-6\amp=0 \end{align*}Next, we check and see that we cannot factor the left side or use the square root property so we must use the quadratic formula. We identify that \(\substitute{a=1}\text{,}\) \(\substitute{b=4}\text{,}\) and \(\substitute{c=-6}\text{.}\) We will substitute them into the quadratic formula:
\begin{align*} x\amp=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ x\amp=\frac{-\substitute{4}\pm\sqrt{(\substitute{4})^2-4(\substitute{1})(\substitute{-6})}}{2(\substitute{1})}\\ \amp=\frac{-4\pm\sqrt{16+24}}{2}\\ \amp=\frac{-4\pm\sqrt{40}}{2}\\ \amp=\frac{-4\pm\sqrt{\highlight{4}\cdot10}}{2}\\ \amp=\frac{-4\pm\sqrt{\highlight{4}}\cdot\sqrt{10}}{2}\\ \amp=\frac{-4\pm\highlight{2}\sqrt{10}}{2}\\ \amp=-\frac{4}{2}\pm\frac{2\sqrt{10}}{2}\\ \amp=-2\pm\sqrt{10} \end{align*}So the solution set is \(\left\{-2+\sqrt{10},-2-\sqrt{10}\right\}\text{.}\)
-
Since the equation \(5x^2-2x+1=0\) is already in standard form, we check and see that we cannot factor the left side or use the square root property so we must use the quadratic formula. We identify that \(\substitute{a=5}\text{,}\) \(\substitute{b=-2}\text{,}\) and \(\substitute{c=1}\text{.}\) We will substitute them into the quadratic formula:
\begin{align*} x\amp=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ x\amp=\frac{-\substitute{(-2)}\pm\sqrt{\substitute{(-2)}^2-4(\substitute{5})(\substitute{1})}}{2(\substitute{5})}\\ \amp=\frac{2\pm\sqrt{4-20}}{10}\\ \amp=\frac{2\pm\sqrt{-16}}{10} \end{align*}Since the solutions have square roots of negative numbers, we must conclude that there are no real solutions.
Example 9.8.12. Recognizing Linear and Quadratic Equations.
Identify which equations are linear, which are quadratic, and which are neither.
\(\displaystyle 2(x-3)^2-5x=6\)
\(\displaystyle 2(x-3)-5x=6\)
\(\displaystyle 2x-6=7x^3\)
\(\displaystyle 2x^2-6=7x^2\)
\(\displaystyle 2\sqrt{x}-x-6=0\)
\(\displaystyle 2x-(x-6)=0\)
\(2(x-3)^2-5x=6\) is quadratic.
\(2(x-3)-5x=6\) is linear.
\(2x-6=7x^3\) is neither linear or quadratic.
\(2x^2-6=7x^2\) is quadratic.
\(2\sqrt{x}-x-6=0\) is neither linear or quadratic.
\(2x-(x-6)=0\) is linear.
Example 9.8.13. Solving Linear and Quadratic Equations.
Use Process 9.3.11 to help solve the equations after deciding if they are linear or quadratic.
\(\displaystyle 4x^2-11x+6=0\)
\(\displaystyle 2(x-6)^2-16=0\)
\(\displaystyle 2(x-6)-16=0\)
\(\displaystyle 3(x-4)^2-15x=0\)
-
To solve the equation \(4x^2-11x+6=0\) we first note that it is quadratic. Since there is a linear term (\(-11x\)), we must use either factoring or the quadratic formula, and we will try factoring first. Since the leading coefficient is \(4\text{,}\) we will try the AC method. In this case, \(ac=24\text{:}\) numbers that multiply to be \(24\) and add to be \(-11\) are \(-8\) and \(-3\text{.}\) So we split up th equation like this:
\begin{align*} 4x^2-11x+6\amp=0\\ 4x^2\mathbin{\highlight{-}}\mathbin{\highlight{8x-3x}}+6\amp=0\\ \left(4x^2\mathbin{\highlight{-}}\mathbin{\highlight{8x}}\right)+(\mathbin{\highlight{-}}\mathbin{\highlight{3x}}+6)\amp=0\\ 4x(x-2)-3(x-2)\amp=0\\ (x-2)(4x-3)\amp=0 \end{align*}\begin{align*} x-2\amp=0 \amp \text{ or } \amp\amp 4x-3\amp=0\\ x\amp=2 \amp \text{ or } \amp\amp x\amp=\frac{3}{4} \end{align*}So, the solution set is \(\left\{2,\frac{3}{4}\right\}\text{.}\)
-
To solve the equation \(2(x-6)^2-16=0\) we first note that it is quadratic. Since there is no linear term, we should try using the square root method.
\begin{align*} 2(x-6)^2-16\amp=0\\ 2(x-6)^2\amp=16\\ (x-6)^2\amp=8 \end{align*}\begin{align*} x-6\amp=\sqrt{8} \amp \text{ or } \amp\amp x-6\amp=-\sqrt{8}\\ x-6\amp=\sqrt{\highlight{4}\cdot2} \amp \text{ or } \amp\amp x-6\amp=-\sqrt{\highlight{4}\cdot2}\\ x-6\amp=\sqrt{\highlight{4}}\cdot\sqrt{2} \amp \text{ or } \amp\amp x-6\amp=-\sqrt{\highlight{4}}\cdot\sqrt{2}\\ x-6\amp=\highlight{2}\sqrt{2} \amp \text{ or } \amp\amp x-6\amp=-\highlight{2}\sqrt{2}\\ x\amp=6+\highlight{2}\sqrt{2} \amp \text{ or } \amp\amp x\amp=6-\highlight{2}\sqrt{2} \end{align*}So, the solution set is \(\left\{6+2\sqrt{2},6-2\sqrt{2}\right\}\text{.}\)
-
To solve the equation \(2(x-6)-16=0\) we first note that it is linear. Since it is linear, we just need to isolate the terms with the variable on one side and all the other terms on the other side of the equals sign.
\begin{gather*} 2(x-6)-16=0\\ 2x-12-16=0\\ 2x-28=0\\ 2x=28\\ x=14 \end{gather*}So, the solution set is \(\{14\}\text{.}\)
-
To solve the equation \(2(x-6)^2-15x=0\) we first note that it is quadratic. Since there is a linear term, we must use either factoring or the quadratic formula. Before we can decide which to use, we need to put the equation in standard form:
\begin{align*} 3(x-4)^2-15x=0\\ 3(x-4)(x-4)-15x=0\\ 3(x^2-8x+16)-15x=0\\ 3x^2-24x+48-15x=0\\ 3x^2-39x+48=0\\ \end{align*}Now we can see that the left hand side does not factor easily, so we will fall back on the quadratic formula. We identify that \(\substitute{a=3}\text{,}\) \(\substitute{b=-39}\text{,}\) and \(\substitute{c=48}\text{.}\)
\begin{align*} x\amp=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ x\amp=\frac{-\substitute{(-39)}\pm\sqrt{\substitute{(-39)}^2-4(\substitute{3})(\substitute{48})}}{2(\substitute{3})}\\ \amp=\frac{39\pm\sqrt{1521-576}}{6}\\ \amp=\frac{39\pm\sqrt{945}}{6}\\ \amp=\frac{39\pm\sqrt{\highlight{9}\cdot105}}{6}\\ \amp=\frac{39\pm\sqrt{\highlight{9}}\cdot\sqrt{105}}{6}\\ \amp=\frac{39\pm3\sqrt{105}}{6} \end{align*}So the solution set is \(\left\{\frac{39+3\sqrt{105}}{6},\frac{39-3\sqrt{105}}{6}\right\}\text{.}\)
Subsection 9.8.4 Complex Solutions to Quadratic Equations
In Section 9.4 we covered what both imaginary numbers and complex numbers are, as well as how to solve quadratic equations where the solutions are imaginary numbers or complex numbers.
Example 9.8.14. Imaginary Numbers.
Simplify the expression \(\sqrt{-12}\) using the imaginary number, \(i\text{.}\)
Start by splitting the \(-1\) from the \(12\) and by looking for the largest perfect-square factor of \(-12\text{,}\) which happens to be \(4\text{.}\)
Example 9.8.15. Solving Quadratic Equations with Imaginary Solutions.
Solve for \(m\) in \(2m^2+16=0\text{,}\) where \(p\) is an imaginary number.
There is no \(m\) term so we will use the square root method.
The solution set is \(\left\{-\highlight{2}\lighthigh{i}\sqrt{2},\highlight{2}\lighthigh{i}\sqrt{2}\right\}\text{.}\)
Example 9.8.16. Solving Quadratic Equations with Complex Solutions.
Solve the equation \(3(v-2)^2+54=0\text{,}\) where \(v\) is a complex number.
So, the solution set is \(\left\{2+\highlight{3}\lighthigh{i}\sqrt{2},2-\highlight{3}\lighthigh{i}\sqrt{2}\right\}\text{.}\)
Subsection 9.8.5 Strategies for Solving Quadratic Equations
In Section 9.5 we review all three methods for solving quadratic equations that we know. For the full explanation of solving using the factoring, visit Section 7.7, solving using the square root method, visit Section 9.2, and for more on the quadratic formula, visit Section 9.3.
Example 9.8.17. How to Choose a Method for Solving a Quadratic Equation.
Solve the quadratic equations using an effective method.
\(\displaystyle (x-4)^2-2=0\)
\(\displaystyle (x-4)^2-2x=0\)
\(\displaystyle (x-4)^2+2x=0\)
All three of the equations here are very similar, so we will need to examine them closely to choose the best method for solving them.
-
To solve the equation \((x-4)^2-2=0\text{,}\) first note that there is no linear term: there is only a square and a constant. This leads us to consider the square root method. Before doing that, isolate the square:
\begin{align*} (x-4)^2-2\amp=0\\ (x-4)^2\amp=2 \end{align*}Now we can apply the square root method to the equation.
\begin{align*} x-4\amp=\sqrt{2}\amp\text{ or }\amp\amp x-4\amp=-\sqrt{2}\\ x\amp=4+\sqrt{2}\amp\text{ or }\amp\amp x\amp=4-\sqrt{2} \end{align*}So the solution set is \(\left\{4+\sqrt{2},4-\sqrt{2}\right\}\)
-
To solve the equation \((x-4)^2-2x=0\text{,}\) first note that there is a linear term (\(-2x\)), so we must use either factoring or the quadratic formula. To use either, we must first put the equation in standard form.
\begin{align*} (x-4)^2-2x\amp=0\\ (x-4)(x-4)-2x\amp=0\\ x^2-8x+16-2x\amp=0\\ x^2-10x+16\amp=0 \end{align*}Now that the equation is in standard form, we can decide whether to use factoring or the quadratic formula. While the quadratic formula always works, it can take more time than factoring if factoring is possible. In this case, factoring entails answering the question “are there two integers that multiply to be \(16\) and add to be \(-10\text{?}\)” The answer is “yes” : \(-8\) and \(-2\) are such numbers.
\begin{align*} x^2-10x+16\amp=0\\ (x-8)(x-2)\amp=0 \end{align*}\begin{align*} x-8\amp=0\amp\text{ or }\amp\amp x-2\amp=0\\ x\amp=8\amp\text{ or }\amp\amp x\amp=2 \end{align*}So the solution set is \(\{2,8\}\text{.}\)
-
To solve the equation \((x-4)^2+2x=0\text{,}\) first note that there is a linear term (\(+2x\)), so we must use either factoring or the quadratic formula. To use either, we must first put the equation in standard form.
\begin{align*} (x-4)^2+2x\amp=0\\ (x-4)(x-4)+2x\amp=0\\ x^2-8x+16+2x\amp=0\\ x^2-6x+16\amp=0 \end{align*}Now that the equation is in standard form, we can decide whether to use factoring or the quadratic formula. In this case, factoring entails answering the question “are there two integers that multiply to be \(16\) and add to be \(-6\text{?}\)” The answer is “no,” so we must use the quadratic formula. First, identify that \(\substitute{a=1}\text{,}\) \(\substitute{b=-6}\text{,}\) and \(\substitute{c=16}\text{.}\)
\begin{align*} x\amp=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ x\amp=\frac{-(\substitute{-6})\pm\sqrt{(\substitute{-6})^2-4(\substitute{1})(\substitute{16})}}{2(\substitute{1})}\\ \amp=\frac{6\pm\sqrt{36-48}}{2}\\ \amp=\frac{6\pm\sqrt{-12}}{2}\\ \end{align*}At this point, we notice that the solutions are complex. Continue to simplify until they are completely reduced.
\begin{align*} x\amp=\frac{6\pm\sqrt{\highlight{4}\cdot\lighthigh{-1}\cdot3}}{2}\\ \amp=\frac{6\pm\sqrt{\highlight{4}}\cdot\sqrt{\lighthigh{-1}}\cdot\sqrt{3}}{2}\\ \amp=\frac{6\pm\highlight{2}\lighthigh{i}\sqrt{3}}{2}\\ \amp=\frac{6}{2}\pm\frac{2i\sqrt{3}}{2}\\ \amp=3\pm i\sqrt{3} \end{align*}So the solution set is \(\left\{3+i\sqrt{3},3-i\sqrt{3}\right\}\text{.}\)
Subsection 9.8.6 Properties of Quadratic Functions
In Section 9.6 we covered the definition of a quadratic function, and how to determine the direction, vertex, axis of symmetry, and vertical and horizontal intercepts. We then learned how to algebraically find the vertex, how to graph a parabola using a table, and how to find the domain and range of quadratic functions.
Example 9.8.18. Finding the Vertex and Axis of Symmetry.
Algebraically find the vertex of the parabola described by the quadratic function \(f(x)=3x^2+8x-7\text{.}\)
To find the vertex of a parabola algebraically, we use the formula \(h=-\frac{b}{2a}\) to find the axis of symmetry first. For our equation, \(\substitute{a=3}\) and \(\lighthigh{b=8}\text{,}\) so:
Next, we evaluate \(f\mathopen{}\left(\substitute{-\frac{4}{3}}\right)\mathclose{}\) to find the \(y\)-coordinate of the vertex.
So, the parabola has its axis of symmetry at \(x=-\frac{4}{3}\) and has its vertex at the point \(\left(-\frac{4}{3},-\frac{37}{3}\right)\text{.}\)
Example 9.8.19. Properties of Quadratic Functions.
Identify the key features of the quadratic function \(y=-2x^2-4x+6\) shown in Figure 9.8.20.
First, we see that this parabola opens downward because the leading coefficient is negative.
Then we locate the vertex which is the point \((-1,8)\text{.}\) The axis of symmetry is the vertical line \(x=-1\text{.}\)
The vertical intercept or \(y\)-intercept is the point \((0,6)\text{.}\)
The horizontal intercepts are the points \((-3,0)\) and \((1,0)\text{.}\)
Example 9.8.22. Graphing Quadratic Functions by Making a Table.
Determine the vertex and axis of symmetry for the quadratic function \(g(x)=2x^2+8x+2\text{.}\) Then make a table of values and sketch the graph of the function.
To determine the vertex of \(g(x)=2x^2+8x+2\text{,}\) we want to find the \(x\)-value of the vertex first. We will use \(h=-\frac{b}{2a}\) for \(\substitute{a=2}\) and \(\lighthigh{b=8}\text{:}\)
To find the vertex, we evaluate \(g(\substitute{-2})\text{.}\)
Now we know that our axis of symmetry is the line \(x=-2\) and the vertex is the point \((-2,-6)\text{.}\) We will set up our table with two values on each side of \(x=-2\text{.}\) We choose \(x= -4, -3, \highlight{-2}, -1\text{,}\) and \(0\text{.}\) Then, we'll determine the \(y\)-coordinates by replacing \(x\) with each value and we have the complete table as shown in Table 9.8.23. Notice that each pair of \(y\)-values on either side of the vertex match. This helps us to check that our vertex and \(y\)-values are correct.
| \(x\) | \(g(x)=2x^2+8x+2\) | Point |
| \(-4\) | \(g(\substitute{-4})=2(\substitute{-4})^2+8(\substitute{-4})+2=2\) | \((-4,2)\) |
| \(-3\) | \(g(\substitute{-3})=2(\substitute{-3})^2+8(\substitute{-3})+2=-4\) | \((-3,-4)\) |
| \(-2\) | \(g(\substitute{-2})=2(\substitute{-2})^2+8(\substitute{-2})+2=-6\) | \((-2,-6)\) |
| \(-1\) | \(g(\substitute{-1})=2(\substitute{-1})^2+8(\substitute{-1})+2=-4\) | \((-1,-4)\) |
| \(0\) | \(g(\substitute{0})=2(\substitute{0})^2+8(\substitute{0})+2=2\) | \((0,2)\) |
Now that we have our table, we will plot the points and draw in the axis of symmetry as shown in Figure 9.8.24. We complete the graph by drawing a smooth curve through the points and drawing an arrow on each end as shown in Figure 9.8.25
Subsection 9.8.7 Graphing Quadratic Functions
In Section 9.7 we covered how to find the vertical and horizontal intercepts of a quadratic function algebraically, how to make a graph of a parabola using key features, applications of quadratic functions and what their real world domains and ranges mean, and how to tell a quadratic function from other types of functions.
Example 9.8.26. Finding the Vertical and Horizontal Intercepts Algebraically.
Algebraically determine the vertical and horizontal intercepts of the quadratic function \(h(x)=6x^2-13x+6\text{.}\)
Algebraically determine the vertical and horizontal intercepts of the quadratic function \(k(x)=2x^2-2x-5\text{.}\)
-
To find the vertical intercept, we evaluate the function when \(x=0\text{.}\) \(h(\substitute{0})=6(\substitute{0})^2-13(\substitute{0})+6=6\text{.}\) So, the vertical intercept of \(h\) is \((0,6)\text{.}\)
Next, to find the horizontal intercepts, we set the function equal to zero. To solve that equation we will use Process 9.5.1. For this particular example, we will practice factoring using the AC method. Here, \(ac=36\) and factor pairs that add up to \(-13\) are \(-9\) and \(-4\text{,}\) as you will see.
\begin{align*} \substitute{h(x)}\amp=6x^2-13x+6\\ \substitute{0}\amp=6x^2\mathbin{\highlight{-}}\mathbin{\highlight{13x}}+6\\ 0\amp=6x^2\mathbin{\highlight{-}}\mathbin{\highlight{9x}}\mathbin{\highlight{-}}\mathbin{\highlight{4x}}+6\\ 0\amp=3x\highlight{(2x-3)}-2\highlight{(2x-3)}\\ 0\amp=(3x-2)\highlight{(2x-3)} \end{align*}\begin{align*} 0\amp=3x-2\amp\text{ or }\amp\amp0\amp=2x-3\\ x\amp=\frac{2}{3}\amp\text{ or }\amp\amp x\amp=\frac{3}{2} \end{align*}So, the horizontal intercepts are \(\left(\frac{2}{3},0\right)\) and \(\left(\frac{3}{2},0\right)\text{.}\)
-
To find the vertical intercept, we have to evaluate the function when \(x=0\text{.}\) \(k(\substitute{0})=2(\substitute{0})^2-2(\substitute{0})-5=-5\text{.}\) So, the vertical intercept of \(k\) is \((0,-5)\text{.}\)
Next, to find the horizontal intercepts, we set the function equal to zero. To solve that equation we will use Process 9.5.1. For this particular example, we will use the quadratic formula because the square root method will not work (because there is a linear term) and factoring fails.
\begin{align*} \substitute{k(x)}\amp=2x^2-2x-5\\ \substitute{0}\amp=2x^2-2x-5\\ \end{align*}We identify that \(\substitute{a=2}\text{,}\) \(\lighthigh{b=-2}\text{,}\) and \(c=-5\)
\begin{align*} x\amp=\frac{-\lighthigh{b}\pm\sqrt{\lighthigh{b}^2-4\substitute{a}c}}{2\substitute{a}}\\ x\amp=\frac{-(\lighthigh{-2})\pm\sqrt{(\lighthigh{-2})^2-4(\substitute{2})(-5)}}{2(\substitute{2})}\\ x\amp=\frac{2\pm\sqrt{4+40}}{4}\\ x\amp=\frac{2\pm\sqrt{44}}{4}\\ x\amp=\frac{2\pm\highlight{2}\sqrt{11}}{4}\\ x\amp=\frac{2}{4}\pm\frac{2\sqrt{11}}{4}\\ x\amp=\frac{1}{2}\pm\frac{\sqrt{11}}{2}\\ x\amp=\frac{1\pm\sqrt{11}}{2} \end{align*}So, the horizontal intercepts are \(\left(\frac{1+\sqrt{11}}{2},0\right)\) and \(\left(\frac{1-\sqrt{11}}{2},0\right)\text{.}\) If you wanted to graph these points, you would need to approximate them as \(\left(2.16,0\right)\) and \(\left(-1.16,0\right)\text{.}\)
Example 9.8.27. Graphing Quadratic Functions Using their Key Features.
Graph the function \(j(x)=-2x^2+6x+8\) by algebraically determining its key features.
To start, we'll note that this function will open downward, as the leading coefficient is negative.
To find the \(y\)-intercept, we'll evaluate \(j(0)\text{:}\) \(j(\substitute{0})=-2(\substitute{0})^2+6(\substitute{0})+8=8\text{.}\) The \(y\)-intercept is \((0,8)\text{.}\)
Next, we'll find the horizontal intercepts by setting \(j(x)=0\) and solving for \(x\text{:}\)
The \(x\)-intercepts are \((4,0)\) and \((-1,0)\text{.}\)
Lastly, we'll determine the vertex. Noting that \(\substitute{a=-2}\) and \(\lighthigh{b=6}\text{,}\) we have:
Using the \(x\)-value \(\substitute{1.5}\) to find the \(y\)-coordinate, we have: \(j(\substitute{1.5})=-2(\substitute{1.5})^2+6(\substitute{1.5})+8=12.5\text{.}\) The vertex is the point \((1.5,12.5)\text{,}\) and the axis of symmetry is the line \(x=1.5\text{.}\)
We're now ready to graph this function. We'll start by drawing and scaling the axes so all of our key features will be displayed as shown in Figure 9.8.28. Next, we'll plot these key points as shown in Figure 9.8.29. Finally, we'll note that this parabola opens downward and connect these points with a smooth curve, as shown in Figure 9.8.30.
Example 9.8.31. Applications of Quadratic Functions.
The Five-hundred-meter Aperture Spherical Telescope 1 (FAST) located in SW China is the worlds largest radio telescope. The name is actually incorrect because it is not spherical: it is parabolic! Parabolic telescopic dishes are very common because parabolas have the unique feature that they focus light coming in at a single point where a collecting instrument is placed.
If a scientist somehow managed to climb to the rim of the dish and roll a ball from the top down toward the center, her ball would travel along the parabola \(h(x)=0.0018x^2-0.9x\text{,}\) where \(x\) is the horizontal distance from the rim of the dish where the ball was released, in meters, and \(h(x)\) is the height of the ball above above the rim, in meters (so negative height would mean below the rim). Note that this is an approximation based on real data.
Find and interpret the vertical intercept of the graph.
Find and interpret the horizontal intercepts of the graph.
Find and interpret the vertex of the graph.
The vertical intercept is found when \(\substitute{x=0}\text{.}\) \(h(\substitute{0})=0.0018(\substitute{0})^2-0.9(\substitute{0})=0\text{.}\) So the vertical intercept is \((0,0)\) which means that the ball was released \(0\) meters from the rim (on the rim) at a height of \(0\) meters above the rim (again, on the rim).
-
The horizontal intercepts are found when \(h(x)=0\text{.}\) This will be a quadratic equation that we can solve using factoring.
\begin{align*} h(x)\amp=0\\ 0.0018x^2-0.9x\amp=0\\ x\left(0.0018x-0.9\right)\amp=0 \end{align*}\begin{align*} x\amp=0\amp\text{ or }\amp\amp 0.0018x-0.9\amp=0\\ x\amp=0\amp\text{ or }\amp\amp 0.0018x\amp=0.9\\ x\amp=0\amp\text{ or }\amp\amp x\amp=500 \end{align*}The horizontal intercepts are \((0,0)\) and \((500,0)\text{.}\) The interpretation of \((0,0)\) is the same as before. The interpretation of \((500,0)\) is that the other side of the rim of the dish is \(500\) meters away. If the ball were to somehow roll all the way down, and then back up the other side, it would pop up at the opposite rim exactly \(500\) meters horizontally away.
-
The vertex is found when the \(x\)-value is at the axis of symmetry. To find that, we use the formula \(x=-\frac{\lighthigh{b}}{2\substitute{a}}\) where \(\substitute{a=0.0018}\) and \(\lighthigh{b=-0.9}\)
\begin{align*} x\amp=-\frac{\lighthigh{b}}{2\substitute{a}}\\ x\amp=-\frac{\lighthigh{-0.9}}{2(\substitute{0.0018})}\\ \amp=250 \end{align*}Then, to find the \(y\)-value, we substitute that \(x\)-value, \(\substitute{250}\) into the original function.
\begin{align*} h(\substitute{250})\amp=0.0018(\substitute{250})^2-0.9(\substitute{250})\\ \amp=-112.5 \end{align*}The vertex is the point \((250,-112.5)\text{.}\) Since the vale of \(a\) is positive, we know that this parabola opens upward. This means that the vertex is the lowest point on the graph. So the lowest point of the telescope dish is \(250\) meters from the rim (horizontally) and \(112.5\) meters below the height of the rim.
Example 9.8.32. Distinguishing Quadratic Functions from Other Functions and Relations.
Decide if the equations represent quadratic functions or something else.
\(\displaystyle y-1=3(x-2)-5\)
\(\displaystyle y=3(x-2)^2-5\)
\(\displaystyle y=\sqrt{x-2}-5\)
\(\displaystyle y^2=x^2-5\)
Recall that Definition 9.6.1 says that a quadratic function has the form \(f(x)=ax^2+bx+c\) where \(a\text{,}\) \(b\text{,}\) and \(c\) are real numbers, and \(a \neq 0\text{.}\)
The equation \(y-1=3(x-2)-5\) is not quadratic. It is in fact a linear equation.
The equation \(y=3(x-2)^2-5\) is quadratic. We could simplify the right hand side and would have something of the form \(y=ax^2+bx+c\text{.}\)
The equation \(y=\sqrt{x-2}-5\) is not quadratic. The \(x\) is inside a radical, not squared, so it cannot be converted into the form \(y=ax^2+bx+c\text{.}\)
The equation \(y^2=x^2-5\) is not quadratic. It cannot be re-written in the form \(y=ax^2+bx+c\) (due to the \(y^2\) term).
Exercises 9.8.8 Exercises
1.
A rectangle’s base is \({9\ {\rm in}}\) shorter than four times its height. The rectangle’s area is \({28\ {\rm in^{2}}}\text{.}\) Find this rectangle’s dimensions.
The rectangle’s height is .
The rectangle’s base is .
2.
A rectangle’s base is \({7\ {\rm in}}\) shorter than twice its height. The rectangle’s area is \({15\ {\rm in^{2}}}\text{.}\) Find this rectangle’s dimensions.
The rectangle’s height is .
The rectangle’s base is .
Square Root Properties
3.
Without using a calculator, estimate the value of \(\sqrt{103}\text{:}\)
9.15
10.85
9.85
10.15
4.
Without using a calculator, estimate the value of \(\sqrt{14}\text{:}\)
3.74
4.26
3.26
4.74
5.
Evaluate the following.
\(\displaystyle{\sqrt{{{\frac{4}{25}}}}={}}\).
6.
Evaluate the following.
\(\displaystyle{\sqrt{{{\frac{9}{100}}}}={}}\).
7.
Evaluate the following.
\(\sqrt{-36}=\).
8.
Evaluate the following.
\(\sqrt{-49}=\).
9.
Simplify the radical expression or state that it is not a real number.
\(\displaystyle{ \frac{{\sqrt{5}}}{{\sqrt{80}}} =}\)
10.
Simplify the radical expression or state that it is not a real number.
\(\displaystyle{ \frac{{\sqrt{3}}}{{\sqrt{75}}} =}\)
11.
Simplify the radical expression or state that it is not a real number.
\(\displaystyle{ {\sqrt{44}} = }\)
12.
Simplify the radical expression or state that it is not a real number.
\(\displaystyle{ {\sqrt{325}} = }\)
13.
Simplify the expression.
\(\displaystyle{2\sqrt{5} \cdot 3\sqrt{90}=}\)
14.
Simplify the expression.
\(\displaystyle{2\sqrt{5} \cdot 5\sqrt{40}=}\)
15.
Simplify the expression.
\(\displaystyle{ {\sqrt{\frac{15}{19}}} \cdot {\sqrt{\frac{3}{19}}} =}\)
16.
Simplify the expression.
\(\displaystyle{ {\sqrt{\frac{21}{11}}} \cdot {\sqrt{\frac{3}{11}}} =}\)
17.
Simplify the expression.
\(\displaystyle{{\sqrt{108}} + {\sqrt{75}} =}\)
18.
Simplify the expression.
\(\displaystyle{{\sqrt{80}} + {\sqrt{20}} =}\)
19.
Simplify the expression.
\(\displaystyle{{\sqrt{63}} - {\sqrt{112}} =}\)
20.
Simplify the expression.
\(\displaystyle{{\sqrt{539}} - {\sqrt{99}} =}\)
21.
Rationalize the denominator and simplify the expression.
\(\displaystyle{ \frac{1}{\sqrt{10}} = }\)
22.
Rationalize the denominator and simplify the expression.
\(\displaystyle{ \frac{1}{\sqrt{2}} = }\)
23.
Rationalize the denominator and simplify the expression.
\(\displaystyle{ \frac{9}{2\sqrt{2}} = }\)
24.
Rationalize the denominator and simplify the expression.
\(\displaystyle{ \frac{7}{8\sqrt{3}} = }\)
25.
Rationalize the denominator and simplify the expression.
\(\displaystyle{ \frac{1}{{\sqrt{18}}} = }\)
26.
Rationalize the denominator and simplify the expression.
\(\displaystyle{ \frac{1}{{\sqrt{112}}} = }\)
27.
Expand and simplify the expression.
\(\displaystyle{\left(6 - {\sqrt{6}}\right)\left(10 - 5 {\sqrt{6}}\right) =}\)
28.
Expand and simplify the expression.
\(\displaystyle{\left(3 - {\sqrt{7}}\right)\left(8 - 2 {\sqrt{7}}\right) =}\)
29.
Expand and simplify the expression.
\(\displaystyle{\left({\sqrt{13}} + {\sqrt{11}}\right)\left({\sqrt{13}} - {\sqrt{11}}\right) =}\)
30.
Expand and simplify the expression.
\(\displaystyle{\left({\sqrt{13}} + {\sqrt{7}}\right)\left({\sqrt{13}} - {\sqrt{7}}\right) =}\)
Solving Quadratic Equations by Using a Square Root
31.
Solve the equation.
\(x^2 = 12\)
32.
Solve the equation.
\(x^2 = 44\)
33.
Solve the equation.
\(25x^2 = 36\)
34.
Solve the equation.
\(81x^2 = 4\)
35.
Solve the equation.
\(\left(x - 1\right)^2 = 81\)
36.
Solve the equation.
\(\left(x+2\right)^2 = 25\)
37.
Solve the equation.
\(46 - 6 ( r+9 )^2 = -8\)
38.
Solve the equation.
\(27 - 5 ( t+9 )^2 = 7\)
39.

Find the value of \(x\text{.}\)
\(x={}\)
40.
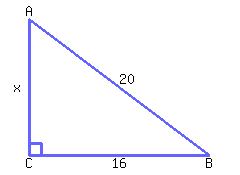
Find the value of \(x\text{.}\)
\(x={}\)
41.
Ken is designing a rectangular garden. The garden’s diagonal must be \(2.6\) feet, and the ratio between the garden’s base and height must be \(12:5\text{.}\) Find the length of the garden’s base and height.
The garden’s base is feet and its height is .
42.
Dennis is designing a rectangular garden. The garden’s diagonal must be \(15\) feet, and the ratio between the garden’s base and height must be \(4:3\text{.}\) Find the length of the garden’s base and height.
The garden’s base is feet and its height is .
The Quadratic Formula
43.
Solve the equation.
\({30x^{2}+43x-8}=0\)
44.
Solve the equation.
\({27x^{2}-12x-4}=0\)
45.
Solve the equation.
\({x^{2}}= {-\left(9x+16\right)}\)
46.
Solve the equation.
\({x^{2}}= {2-3x}\)
47.
Solve the equation.
\({3x^{2}+5x+4}= 0\)
48.
Solve the equation.
\({3x^{2}+3x+4}= 0\)
49.
Solve the equation.
\({10x+10} = {x+91}\)
50.
Solve the equation.
\({8y+5} = {y+47}\)
51.
Solve the equation.
\(2-2x^2 = -5\)
52.
Solve the equation.
\(12-7y^2 = 10\)
53.
Solve the equation.
\(x^2 - 6x= 0\)
54.
Solve the equation.
\(x^2+14x= 0\)
55.
Solve the equation.
\({x^{2}-4x} = {32}\)
56.
Solve the equation.
\({x^{2}+2x} = {24}\)
57.
Solve the equation.
\(\left(x+9\right)^2 = 4\)
58.
Solve the equation.
\(\left(x - 10\right)^2 = 81\)
59.
Solve the equation.
\({x^{2}}= {-\left(9x+17\right)}\)
60.
Solve the equation.
\({x^{2}}= {-\left(5x+3\right)}\)
61.
An object is launched upward at the height of \(270\) meters. Its height can be modeled by
where \(h\) stands for the object’s height in meters, and \(t\) stands for time passed in seconds since its launch. The object’s height will be \(320\) meters twice before it hits the ground. Find how many seconds since the launch would the object’s height be \(320\) meters. Round your answers to two decimal places if needed.
The object’s height would be \(320\) meters the first time at seconds, and then the second time at seconds.
62.
An object is launched upward at the height of \(290\) meters. Its height can be modeled by
where \(h\) stands for the object’s height in meters, and \(t\) stands for time passed in seconds since its launch. The object’s height will be \(310\) meters twice before it hits the ground. Find how many seconds since the launch would the object’s height be \(310\) meters. Round your answers to two decimal places if needed.
The object’s height would be \(310\) meters the first time at seconds, and then the second time at seconds.
Complex Solutions to Quadratic Equations
63.
Simplify the radical and write it as a complex number using \(i\text{.}\)
\(\displaystyle{ \sqrt{-27} =}\)
64.
Simplify the radical and write it as a complex number using \(i\text{.}\)
\(\displaystyle{ \sqrt{-48} =}\)
65.
Solve the quadratic equation. Solutions could be complex numbers.
\({-t^{2}} - 9 = -6\)
66.
Solve the quadratic equation. Solutions could be complex numbers.
\({-4t^{2}} - 4 = 8\)
67.
Solve the quadratic equation. Solutions could be complex numbers.
\(-9(x - 10)^2+1 = 442\)
68.
Solve the quadratic equation. Solutions could be complex numbers.
\(6(x - 4)^2+1 = -53\)
Strategies for Solving Quadratic Equations
69.
Solve the equation.
\(59x^2 + 11= 0\)
70.
Solve the equation.
\(29x^2 + 17= 0\)
71.
Solve the equation.
\({4x^{2}}={-13x-10}\)
72.
Solve the equation.
\({2x^{2}}={-13x-6}\)
73.
Solve the equation.
\({x^{2}-6x-11}= 0\)
74.
Solve the equation.
\({x^{2}-6x-8}= 0\)
75.
Solve the equation.
\(47 - 5 ( t - 1 )^2 = 2\)
76.
Solve the equation.
\(0 - 4 ( x - 1 )^2 = -4\)
77.
Solve the equation.
\({x^{2}+3x} = {-2}\)
78.
Solve the equation.
\({x^{2}+11x} = {-24}\)
Properties of Quadratic Functions
79.
Find the axis of symmetry and vertex of the quadratic function.
\({y}={-2x^{2}+4x-1}\)
Axis of symmetry:
Vertex:
80.
Find the axis of symmetry and vertex of the quadratic function.
\({y}={-5x^{2}-40x-3}\)
Axis of symmetry:
Vertex:
81.
Find the axis of symmetry and vertex of the quadratic function.
\({y}={x^{2}+3x-2}\)
Axis of symmetry:
Vertex:
82.
Find the axis of symmetry and vertex of the quadratic function.
\({y}={2x^{2}-2x+3}\)
Axis of symmetry:
Vertex:
83.
For \(y=4x^2-8x+5\text{,}\) determine the vertex, create a table of ordered pairs, and then graph the function.
84.
For \(y=2x^2+4x+7\text{,}\) determine the vertex, create a table of ordered pairs, and then graph the function.
85.
For \(y=-x^2+4x+2\text{,}\) determine the vertex, create a table of ordered pairs, and then graph the function.
86.
For \(y=-x^2+2x-5\text{,}\) determine the vertex, create a table of ordered pairs, and then graph the function.
87.
You will build a rectangular sheep enclosure next to a river. There is no need to build a fence along the river, so you only need to build on three sides. You have a total of 480 feet of fence to use. Find the dimensions of the pen such that you can enclose the maximum possible area. One approach is to let \(x\) represent the length of fencing that runs perpendicular to the river, and write an expression for the area of the enclosure. Then find its vertex and interpret it.
The length of the pen (parallel to the river) should be 240 ft, the width (perpendicular to the river) should be 120 ft, and the maximum possible area is .
88.
You will build a rectangular sheep enclosure next to a river. There is no need to build a fence along the river, so you only need to build on three sides. You have a total of 490 feet of fence to use. Find the dimensions of the pen such that you can enclose the maximum possible area. One approach is to let \(x\) represent the length of fencing that runs perpendicular to the river, and write an expression for the area of the enclosure. Then find its vertex and interpret it.
The length of the pen (parallel to the river) should be 245 ft, the width (perpendicular to the river) should be 122.5 ft, and the maximum possible area is .
Graphing Quadratic Functions
89.
Find the \(y\)-intercept and any \(x\)-intercept(s) of the quadratic curve.
\({y}={x^{2}+7x+10}\)
\(y\)-intercept:
\(x\)-intercept(s):
90.
Find the \(y\)-intercept and any \(x\)-intercept(s) of the quadratic curve.
\({y}={-x^{2}+x+20}\)
\(y\)-intercept:
\(x\)-intercept(s):
91.
Find the \(y\)-intercept and any \(x\)-intercept(s) of the quadratic curve.
\({y}={x^{2}+2x+4}\)
\(y\)-intercept:
\(x\)-intercept(s):
92.
Find the \(y\)-intercept and any \(x\)-intercept(s) of the quadratic curve.
\({y}={x^{2}-5x-3}\)
\(y\)-intercept:
\(x\)-intercept(s):
93.
Find the \(y\)-intercept and any \(x\)-intercept(s) of the quadratic curve.
\({y}={16x^{2}+56x+49}\)
\(y\)-intercept:
\(x\)-intercept(s):
94.
Find the \(y\)-intercept and any \(x\)-intercept(s) of the quadratic curve.
\({y}={16x^{2}-1}\)
\(y\)-intercept:
\(x\)-intercept(s):
Graph each curve by algebraically determining its key features.
95.
\(y=x^2-7x+12\)
96.
\(y=x^2+5x-14\)
97.
\(y=-x^2-x+20\)
98.
\(y=-x^2+4x+21\)
99.
\(y=x^2+6x\)
100.
\(y=x^2-8x\)
101.
\(y=x^2+4x+7\)
102.
\(y=x^2-2x+6\)
103.
\(y=2x^2-4x-30\)
104.
\(y=3x^2+21x+36\)
Applications of Quadratic Functions
105.
From an oceanside clifftop \({120\ {\rm m}}\) above sea level, an object was shot into the air with an initial vertical speed of \({235.2\ {\textstyle\frac{\rm\mathstrut m}{\rm\mathstrut s}}}\text{.}\) It fell into the ocean. Its height (above sea level) as time passes can be modeled by the quadratic equation \(y={-4.9t^{2}+235.2t+120}\text{.}\) Here \(t\) represents the number of seconds since the object’s release, and \(y\) represents the object’s height (above sea level) in meters.
After , this object reached its maximum height of .
This object flew for before it landed in the ocean.
This object was above sea level \({23\ {\rm s}}\) after its release.
This object was \({982.4\ {\rm m}}\) above sea level twice: once after its release, and again later after its release.
106.
From an oceanside clifftop \({190\ {\rm m}}\) above sea level, an object was shot into the air with an initial vertical speed of \({254.8\ {\textstyle\frac{\rm\mathstrut m}{\rm\mathstrut s}}}\text{.}\) It fell into the ocean. Its height (above sea level) as time passes can be modeled by the quadratic equation \(y={-4.9t^{2}+254.8t+190}\text{.}\) Here \(t\) represents the number of seconds since the object’s release, and \(y\) represents the object’s height (above sea level) in meters.
After , this object reached its maximum height of .
This object flew for before it landed in the ocean.
This object was above sea level \({47\ {\rm s}}\) after its release.
This object was \({3458.3\ {\rm m}}\) above sea level twice: once after its release, and again later after its release.
