Section 12.2 Compound Inequalities
On the newest version of the SAT (an exam that often qualifies students for colleges) the minimum score that you can earn is \(400\) and the maximum score that you can earn is \(1600\text{.}\) This means that only numbers between \(400\) and \(1600\text{,}\) including these endpoints, are possible scores. To plot all of these values on a number line would look something like:
Going back to the original statement, “the minimum score that you can earn is \(400\) and the maximum score that you can earn is \(1600\text{,}\)” this really says two things. First, it says that \((\text{a SAT score})\geq400\text{,}\) and second, that \((\text{a SAT score})\le1600\text{.}\) When we combine two inequalities like this into a single problem, it becomes a compound inequality.
Our lives are often constrained by the compound inequalities of reality: you need to buy enough materials to complete your project, but you can only fit so much into your vehicle; you would like to finish your degree early, but only have so much money and time to put toward your courses; you would like a vegetable garden big enough to supply you with veggies all summer long, but your yard or balcony only gets so much sun. In the rest of the section, we hope to illuminate how to think mathematically about problems like these.
Before continuing, a review on how notation for intervals works may be useful, and you may benefit from revisiting Section 1.7. Then a refresher on solving linear inequalities may also benefit you, which you can revisit in Section 3.2 and Section 3.3.
Subsection 12.2.1 Unions and Intersections of Intervals
Definition 12.2.2.
The union of two sets, \(A\) and \(B\text{,}\) is the set of all elements contained in either \(A\) or \(B\) (or both). We write \(A\cup B\) to indicate the union of the two sets.
In other words, the union of two sets is what you get if you toss every number in both sets into a bigger set.
Example 12.2.3.
The union of sets \(\{1,2,3,4\}\) and \(\{3,4,5,6\}\) is the set of all elements from either set. So \(\{\highlight{1,2,3,4}\}\cup\{3,4,\highlight{5,6}\}=\{\highlight{1,2,3,4,5,6}\}\text{.}\) Note that we don't write duplicates.
Definition 12.2.4.
The intersection of two sets, \(A\) and \(B\text{,}\) is the set of all elements that are in \(A\) and \(B\text{.}\) We write \(A\cap B\) to indicate the intersection of the two sets.
In other words, the intersection of two sets is where the two sets overlap.
Example 12.2.5.
The intersection of sets \(\{1,2,3,4\}\) and \(\{3,4,5,6\}\) is the set of all elements that are in common to both sets. So \(\{1,2,\highlight{3,4}\}\cap\{\highlight{3,4},5,6\}=\{\highlight{3,4}\}\text{.}\)
Example 12.2.6.
Find the union of the sets \([-3,5)\) and \([2,8)\text{.}\)
To find the union of the sets \([-3,5)\) and \([2,8)\text{,}\) first we draw a number line with both intervals drawn to visualize both sets.
Recall that the union of two sets is the set of the combination of numbers from both sets. Looking at the graph, we need to include all of the numbers from both colored lines. Imagine pressing these two colored lines together as if they were long strands of modeling clay. The new combined strand would go from \(-3\) all the way to \(8\text{.}\) Note that \(-3\) would be included on this new line because it was in \([-3,5)\text{,}\) but \(8\) wouldn't be on this new line because it wasn't on either of the lines.
In conclusion,
Example 12.2.9.
Find the intersection of the sets \([-3,5)\) and \([2,8)\text{.}\)
To find the intersection of the sets \([-3,5)\) and \([2,8)\text{,}\) first we draw a number line with both intervals drawn to visualize the overlap of the sets.
Recall that the intersection of two sets is the set of the numbers in common to both sets. The lines have numbers in common on a long stretch where they overlap. How would we describe all of the numbers where the two lines overlap? In English, we might say that the lines overlap at every number between \(2\) and \(5\text{.}\) Note that the number \(2\) is in both sets, but since \(5\) is not in the set \([-3,5)\text{,}\) we should exclude \(5\) from the intersection. The description we have come up with is the same as the interval \([2,5)\text{.}\)
In conclusion,
Example 12.2.12.
Let's visualize the union of the sets \((-\infty,4)\) and \([7,\infty)\text{.}\) First, we make a number line with both intervals drawn to understand what both sets mean.
The two intervals should be viewed as a single object when stating the union, so here is the picture of the union. It looks the same, but now it is a graph of a single set.
Example 12.2.15.
Find the intersection of the sets \((-\infty,-1)\) and \((-\infty,3)\text{.}\)
To find the intersection of the sets \((-\infty,-1)\) and \((-\infty,3)\text{,}\) first we draw a number line with both intervals drawn to visualize where the sets overlap.
Recall that the intersection of two sets is the set of the numbers in common to both sets. In English, we might say that the lines overlap at every number below \(-1\text{.}\) This description is the same as the interval \((-\infty,-1)\text{.}\)
In conclusion,
Remark 12.2.18.
Note that every intersection of two intervals can and should be simplified in some way. Even if the sets have nothing in common at all, as in \((-\infty,1]\) and \([5,\infty)\text{,}\) their intersection can be written as \((-\infty,1]\cap[5,\infty)=\emptyset\text{.}\) On the other hand, there are some unions which cannot be algebraically simplified. For example, if the two sets have nothing in common, as in \((-\infty,1]\) and \([5,\infty)\) again, then the union is simply \((-\infty,1]\cup[5,\infty)\text{,}\) which is our final simplification.
Example 12.2.19.
Simplify the intersections and unions.
\(\{2,4,6,8\}\cup\{1,2,3,4\}\text{.}\)
\(\{2,4,6,8\}\cap\{1,2,3,4\}\text{.}\)
\(\{2,4,6,8\}\cup\{1,3,5,7\}\text{.}\)
\(\{2,4,6,8\}\cap\{1,3,5,7\}\text{.}\)
\((-\infty,9]\cup[-\infty,-3]\text{.}\)
\((-\infty,9]\cap[-\infty,-3]\text{.}\)
\((-\infty,12)\cup[-3,\infty)\text{.}\)
\((-\infty,12)\cap[-3,\infty)\text{.}\)
\((-\infty,-2]\cup[4,\infty)\text{.}\)
\((-\infty,-2]\cap[4,\infty)\text{.}\)
\([-7,8)\cup(0,12]\text{.}\)
\([-7,8)\cap(0,12]\text{.}\)
\(\{2,4,6,8\}\cup\{1,2,3,4\}=\{1,2,3,4,6,8\}\text{.}\)
\(\{2,4,6,8\}\cap\{1,2,3,4\}=\{2,4\}\text{.}\)
\(\{2,4,6,8\}\cup\{1,3,5,7\}=\{1,2,3,4,5,6,7,8\}\text{.}\)
\(\{2,4,6,8\}\cap\{1,3,5,7\}=\emptyset\text{.}\)
\((-\infty,9]\cup(-\infty,-3]=(-\infty,9]\text{.}\)
\((-\infty,9]\cap(-\infty,-3]=(-\infty,-3]\text{.}\)
\((-\infty,12)\cup[-3,\infty)=\mathbb{R}\text{.}\)
\((-\infty,12)\cap[-3,\infty)=[-3,12)\text{.}\)
\((-\infty,-2]\cup[4,\infty)=(-\infty,-2]\cup[4,\infty)\text{.}\) This union cannot be simplified because the two sets have nothing in common.
\((-\infty,-2]\cap[4,\infty)=\emptyset\text{.}\)
\([-7,8)\cup(0,12]=[-7,12]\text{.}\)
\([-7,8)\cap(0,12]=(0,8)\text{.}\)
Subsection 12.2.2 “Or” Compound Inequalities
Definition 12.2.20.
A compound inequality is a grouping of two or more inequalities into a single inequality statement. These usually come in two flavors: “or” and “and” inequalities. For an example of an “or” compound inequality, you might get a discount at the movie theater if your age is less than \(13\) or greater than \(64\text{.}\) In general, compound inequalities of the “and” variety currently are beyond the scope of this book. However, a special type of the “and” variety is covered later in Subsection 12.2.3.
In math, the technical term or means “either or both.” So, mathematically, if we asked if you would like “chocolate cake or apple pie” for dessert, your choices are either “chocolate cake,” “apple pie,” or “both chocolate cake and apple pie.” This is slightly different than the English “or”, which usually means “one or the other, but not both.”
“Or” shows up in math between equations (as in when solving a quadratic equation, you might end up with “\(x=2\) or \(x=-3\)” ) or between inequalities (which is what we're about to discuss).
Remark 12.2.21.
The definition of “or” is very close to the definition of a union where you combine elements from either or both sets together. In fact, when you have an “or” between inequalities in a compound inequality, to find the solution set of the compound inequality, you find the union of the solutions sets of each of the pieces.
Example 12.2.22.
Solve the compound inequality.
Writing the solution set to this compound inequality doesn't require any algebra beforehand because each of the inequalities is already solved for \(x\text{.}\) The first thing we should do is understand what each inequality is saying using a graph.
An “or” statement becomes a union of solution sets, so the solution set to the compound inequality must be:
Example 12.2.24.
Solve the compound inequality.
First, we need to do some algebra to isolate \(x\) in each piece. Note that we are going to do algebra on both pieces simultaneously. Also note that the mathematical symbol “or” should be written on each line.
The solution set for the compound inequality \(x\lt2\) is \((-\infty,2)\) and the solution set to \(x\ge5\) is \([5,\infty)\text{.}\) To do the “or” portion of the problem, we need to take the union of these two sets. Let's first make a graph of the solution sets to visualize the problem.
The union combines both solution sets into one, and so
We have finished the problem, but for the sake of completeness, let's try to verify that our answer is reasonable.
-
First, let's choose a number that is not in our proposed solution set. We will arbitrarily choose \(\highlight{3}\text{.}\)
\begin{align*} 3-5x\amp\gt-7\amp\text{or}\amp\amp 2-x\amp\le-3\\ 3-5(\highlight{3})\amp\stackrel{?}{\gt}-7\amp\text{or}\amp\amp 2-(\highlight{3})\amp\stackrel{?}{\le}-3\\ -12\amp\stackrel{\text{no}}{\gt}-7\amp\text{or}\amp\amp -1\amp\stackrel{\text{no}}{\le}-3 \end{align*}This value made both inequalities false, which is why \(3\) isn't in our solution set.
-
Next, let's choose a number that is in our solution region. We will arbitrarily choose \(\highlight{1}\text{.}\)
\begin{align*} 3-5x\amp\gt-7\amp\text{or}\amp\amp 2-x\amp\le-3\\ 3-5(\highlight{1})\amp\stackrel{?}{\gt}-7\amp\text{or}\amp\amp 2-(\highlight{1})\amp\stackrel{?}{\le}-3\\ -2\amp\stackrel{\checkmark}{\lt}-7\amp\text{or}\amp\amp 1\amp\stackrel{\text{no}}{\leq}-3 \end{align*}This value made one of the inequalities true. Since this is an “or” statement, only one or the other piece has to be true to make the compound inequality true.
-
Last, what will happen if we choose a value that was in the other solution region in Figure 12.2.25, like the number \(\highlight{6}\text{?}\)
\begin{align*} 3-5x\amp\gt-7\amp\text{or}\amp\amp 2-x\amp\le-3\\ 3-5(\highlight{6})\amp\stackrel{?}{\gt}-7\amp\text{or}\amp\amp 2-(\highlight{6})\amp\stackrel{?}{\le}-3\\ -27\amp\stackrel{\text{no}}{\gt}-7\amp\text{or}\amp\amp -4\amp\stackrel{\checkmark}{\le}-3 \end{align*}This solution made the other inequality piece true.
This completes the check. Numbers from within the solution region make the compound inequality true and numbers outside the solution region make the compound inequality false.
Example 12.2.26.
Solve the compound inequality.
First, we will solve each inequality for \(t\text{.}\) Recall that we usually try to clear denominators by multiplying both sides by the least common denominator.
The solution set to \(t\le \frac{2}{3}\) is \(\left(-\infty,\frac{2}{3}\right]\) and the solution set to \(t\gt 7\) is \((7,\infty)\text{.}\) Figure 12.2.27 shows these two sets.
Note that the two sets do not overlap so there will be no way to simplify the union. Thus, the solution set to the compound inequality is:
Example 12.2.28.
Solve the compound inequality.
First, we solve each inequality for \(y\text{.}\)
The solution set to \(y\gt 7\) is \((7,\infty)\) and the solution set to \(y\le 2\) is \((-\infty,2]\text{.}\) Figure 12.2.29 shows these two sets.
So the solution set to the compound inequality is:
Subsection 12.2.3 Double and “And” Compound Inequalities
The inequality \(1\leq 2\lt 3\) says a lot more than you might think. It actually says four different single inequalities, which are highlighted for you to see.
This might seem trivial at first, but if you are presented with an inequality like \(-1\lt3\geq2\text{,}\) at first it might look sensible; however, in reality, you need to check that all four linear inequalities make sense. Those are highlighted here.
One of these inequalities is false: \(-1\ngeq2\text{.}\) This implies that the entire original inequality, \(-1\lt3\geq2\text{,}\) is nonsense.
Example 12.2.30.
Decide whether or not the following inequalities are true or false.
True or False: \(-5\lt7\le12\text{?}\)
True or False: \(-7\le-10\lt4\text{?}\)
True or False: \(-2\le0\geq1\text{?}\)
True or False: \(5\gt-3\geq-9\text{?}\)
True or False: \(3\lt3\le5\text{?}\)
True or False: \(9\gt1\lt5\text{?}\)
True or False: \(3\lt8\le-2\text{?}\)
True or False: \(-9\lt-4\le-2\text{?}\)
We need to go through all four single inequalities for each. If the inequality is false, for simplicity's sake, we will only highlight the one single inequality that makes the inequality false.
True: \(-5\lt7\le12\text{.}\)
False: \(\highlight{-7}\mathbin{\highlight{\nleq-10}}\mathbin{\lowlight{\lt}}\lowlight{4}\text{.}\)
False: \(\highlight{-2}\mathbin{\lowlight{\le}}\lowlight{0}\mathbin{\highlight{\ngeq}}\highlight{1}\text{.}\)
True: \(5\gt-3\geq-9\text{.}\)
False: \(\highlight{3}\mathbin{\highlight{\nless}}\highlight{3}\mathbin{\lowlight{\le}}\lowlight{5}\text{.}\)
False: \(\highlight{9}\mathbin{\lowlight{\gt}}\lowlight{1}\mathbin{\highlight{\nless}}\highlight{5}\text{.}\)
False: \(\lowlight{3}\mathbin{\lowlight{\lt}}\highlight{8}\mathbin{\highlight{\nleq}}\highlight{-2}\text{.}\)
True: \(-9\lt-4\le-2\text{.}\)
As a general hint, no (nontrivial) double (or three-part) inequality can ever be true if the inequality signs are not pointing in the same direction. So no matter what numbers \(a\text{,}\) \(b\text{,}\) and \(c\) are, both \(a\lt b\geq c\) and \(a\geq b \lt c\) cannot be true! Soon you will be writing inequalities like \(2\lt x \le 4\) and you need to be sure to check that your answer is feasible. You will know that if you get \(2\gt x \le 4\) or \(2\lt x \geq 4\) that something went wrong in the solving process. The only exception is that something like \(1\le1\geq1\) is true because \(1=1=1\text{,}\) although this shouldn't come up very often!
Next, there are two different kinds of “and” compound inequalities. One type has two inequalities joined by the word “and,” like
The other type has an expression that is “between” two values, as we have been discussing in the past examples, like
Remark 12.2.31.
The inequality “\(A \lt B \le C\)” is equivalent to “\(A \lt B\) and \(B\le C\text{,}\)” but we don't need to break it up into the two statements. It can also be read as “B is between A and C.”
Remark 12.2.32.
An “and” statement means that you need both inequalities to be true simultaneously. In English, if you say, “I need Khaleem and Freja to paint the fence,” then the only way you will be happy is if both people are working simultaneously on the fence. This statement that both things happen at the same time should be very reminiscent of our discussion of intersections earlier in this section. In fact, every “and” statement will result in the intersection of the solution sets of the pieces.
Example 12.2.33.
Solve the compound inequality.
The solution set to \(t\lt3\) is \((-\infty,3)\) and the solution set to \(t\geq-1\) is \([-1,\infty)\text{.}\) Shown is a graph of these solution sets.
Recall that an “and” problem finds the intersection of the solution sets. Intersection finds the \(t\)-values where the two lines overlap, so the solution to the compound inequality must be
We have finished the problem, but for the sake of completeness, let's try to “verify” that our answer is reasonable.
-
First, choose a number within our solution region and test that it makes both original inequalities true. We will arbitrarily choose \(\highlight{1}\text{.}\)
\begin{align*} 4-2t\amp\gt -2\amp\text{and}\amp\amp 3t+1\amp\geq -2\\ 4-2(\highlight{1})\amp\stackrel{?}{\gt} -2\amp\text{and}\amp\amp 3(\highlight{1})+1\amp\stackrel{?}{\geq} -2\\ 2\amp\stackrel{\checkmark}{\gt} -2\amp\text{and}\amp\amp 4\amp\stackrel{\checkmark}{\geq} -2 \end{align*} -
Next, choose a value outside the solution set and test that it makes at least one of the inequalities false. We will arbitrarily choose \(\highlight{4}\text{.}\)
\begin{align*} 4-2t\amp\gt -2\amp\text{and}\amp\amp 3t+1\amp\geq -2\\ 4-2(\highlight{4})\amp\stackrel{?}{\gt} -2\amp\text{and}\amp\amp 3(\highlight{4})+1\amp\stackrel{?}{\geq} -2\\ -4\amp\stackrel{\text{no}}{\gt} -2\amp\text{and}\amp\amp 13\amp\stackrel{\checkmark}{\geq} -2 \end{align*}Since one of the inequalities is false and this is an “and” statement, the compound inequality is false for this value, which is what is expected by picking a number outside the solution set.
-
Last, we should choose a number that is not a solution that is on the “other side” of the solution set. We will arbitrarily choose \(\highlight{-2}\text{.}\)
\begin{align*} 4-2t\amp\gt -2\amp\text{and}\amp\amp 3t+1\amp\geq -2\\ 4-2(\highlight{-2})\amp\stackrel{?}{\gt} -2\amp\text{and}\amp\amp 3(\highlight{-2})+1\amp\stackrel{?}{\geq} -2\\ 8\amp\stackrel{\checkmark}{\gt} -2\amp\text{and}\amp\amp -5\amp\stackrel{\text{no}}{\geq} -2 \end{align*}Again, since one of the inequalities is false and this is an “and” statement, the compound inequality is false for \(-2\text{.}\)
So, numbers outside the proposed solution region make the compound inequality false, and numbers inside the region make the compound inequality true. We have verified our solution set.
Example 12.2.35.
Write the solution set to the compound inequality.
The solutions to the double inequality \(-7\lt x\le 5\) are those numbers that are trapped between \(-7\) and \(5\text{,}\) including \(5\) but not \(-7\text{.}\) Keep in mind that there are infinitely many decimal numbers and irrational numbers that satisfy this inequality like \(-2.781828\) and \(\pi\text{.}\) We will write these numbers in interval notation as \((-7,5]\) or in set builder notation as \(\{x\mid -7\lt x\le 5\}\text{.}\)
Example 12.2.36.
Solve the compound inequality.
This is a double (or three-part) inequality, which we can treat just as a regular inequality, but with three “sides.” The goal is to isolate \(x\) in the middle and whatever you do to one “side” you have to do to the other two “sides.”
The solutions to the double inequality \(-1\le x\lt \frac{7}{9}\) are those numbers that are trapped between \(-1\) and \(\frac{7}{9}\text{,}\) including \(-1\) but not \(\frac{7}{9}\text{.}\) The solution set in interval notation is \(\left[-1,\frac{7}{9}\right)\text{.}\)
Example 12.2.37.
Solve the compound inequality.
This is a double inequality, which we can treat just as a regular inequality, but with three “sides.” The goal is to isolate \(x\) in the middle and whatever you do to one “side” you have to do to the other two “sides.” We will begin by canceling the fraction by multiplying each part by the least common denominator.
Notice that we had to reverse the direction of the inequality signs since we divided by a negative number.
Then, at the end, we reverse the entire statement to go from smallest to largest. The solution set is \([-6,15)\text{.}\)
Example 12.2.38.
Solve the compound inequality.
The solution set to \(x\geq -3\) is \([-3,\infty)\) and the solution set to \(x\lt-5\) is \((-\infty,-5)\text{.}\) Shown is a graph of these solution sets on a number line.
Recall that “and” statements of inequalities become intersections of the solution sets. Since intersections refer to where the sets overlap, and these sets never overlap, there must be no solution to the compound inequality. Mathematically, we would say
Subsection 12.2.4 Applications of Compound inequalities
Example 12.2.40.
Raphael's friend is getting married and he's decided to give them some dishes from their registry. Raphael doesn't want to seem cheap, but isn't a wealthy man either, so he wants to buy “enough”, but not “too many.” He's decided that he definitely wants to spend at least \(\$150\) on his friend, but less than \(\$250\text{.}\) Each dish is \(\$21.70\) and shipping on an order of any size is going to be \(\$19.99\text{.}\) Given his budget, set up and algebraically solve a compound inequality to find out what his different options are for the number of dishes that he can buy.
First, we should define our variable. Let \(x\) represent the number of dishes that Raphael can afford. Next we should write a compound inequality that describes this situation. In this case, Raphael wants to spend between \(\$150\) and \(\$250\) and, since he's buying \(x\) dishes, the price that he will pay is \(21.70x+19.99\text{.}\) All of this translates to a double inequality
Now we have to solve this inequality in the usual way.
The interpretation of this inequality is a little tricky. Remember that \(x\) represents the number of dishes Raphael can afford. Since you cannot buy \(5.991\) dishes (manufacturers will typically only ship whole number amounts of tableware) his minimum purchase must be \(6\) dishes. We have a similar problem with his maximum purchase: clearly he cannot buy \(10.6\) dishes. So, should we round up or down? If we rounded up, that would be \(11\) dishes and that would cost \(\$21.70\cdot\highlight{11}+\$19.99=\$258.69\text{,}\) which is outside his price range. Therefore, we should actually round down in this case.
In conclusion, Raphael should buy somewhere between 6 and 10 dishes for his friend to stay within his budget.
Example 12.2.41.
Oak Ridge National Laboratory, a renowned scientific research facility, compiled some data in table 4.28 1 on fuel efficiency of a mid-size hybrid car versus the speed that the car was driven. A model for the fuel efficiency \(e(x)\) (in miles per gallon, mpg) at a speed \(x\) (in miles per hour, mph) is \(e(x)=88-0.7x\text{.}\)
Evaluate and interpret \(e(60)\) in the context of the problem.
Note that this model only applies between certain speeds. The maximum fuel efficiency for which this formula applies is 55 mpg and the minimum fuel efficiency for which it applies is 33 mpg. Set up and algebraically solve a compound inequality to find the range of speeds for which this model applies.
-
Let's evaluate \(e(60)\) first.
\begin{align*} e(x)\amp=88-0.7x\\ e(\highlight{60})\amp=88-0.7(\highlight{60})\\ \amp=46 \end{align*}So, when the hybrid car travels at a speed of 60 mph, it has a fuel efficiency of 46 mpg.
-
In this case, the minimum efficiency is 33 mpg and the maximum efficiency is 55 mpg. We need to trap our formula between these two values to solve for the respective speeds.
\begin{align*} 33 \amp\lt 88-0.7x \lt 55\\ 33\subtractright{88} \amp\lt 88-0.7x\subtractright{88} \lt 55\subtractright{88}\\ -55 \amp\lt -0.7x \lt -33\\ \divideunder{-55}{-0.7} \amp\mathbin{\highlight{\gt}} \divideunder{-0.7x}{-0.7} \mathbin{\highlight{\gt}} \divideunder{-33}{-0.7}\\ 78.57 \amp\gt x \gt 47.14\amp\text{(note: these values are approximate)} \end{align*}
This inequality says that our model is applicable when the car's speed is between about 47 mph and about 79 mph.
Exercises 12.2.5 Exercises
Review and Warmup
1.
For the interval expressed in the number line, write it using set-builder notation and interval notation.
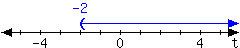
In set-builder notation:
In interval notation:
2.
For the interval expressed in the number line, write it using set-builder notation and interval notation.
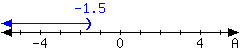
In set-builder notation:
In interval notation:
3.
For the interval expressed in the number line, write it using set-builder notation and interval notation.
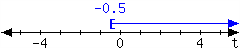
In set-builder notation:
In interval notation:
4.
For the interval expressed in the number line, write it using set-builder notation and interval notation.
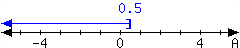
In set-builder notation:
In interval notation:
5.
\({x-4} \leq {8}\)
;
6.
\({x-4} \leq {6}\)
;
7.
\({-5x} \geq {20}\)
;
8.
\({-2x} \geq {6}\)
;
9.
\({2} \geq {-4x+2}\)
;
10.
\({5} \geq {-4x+5}\)
;
11.
\({7t+5} \lt {3t+21}\)
;
12.
\({8t+2} \lt {5t+8}\)
;
Check Solutions
13.
Decide whether the given value for the variable is a solution.
-
\(x \gt 6\quad\text{and}\quad x \leq 7 \qquad x = 2\)
The given value
is
is not
-
\(x \lt 8\quad\text{or}\quad x \geq 8 \qquad x = 3\)
The given value
is
is not
-
\(x \geq -2\quad\text{and}\quad x \leq 3 \qquad x = 1\)
The given value
is
is not
-
\(-2 \leq x \leq 2 \qquad x = -2\)
The given value
is
is not
14.
Decide whether the given value for the variable is a solution.
-
\(x \gt 7\quad\text{and}\quad x \leq 4 \qquad x = 7\)
The given value
is
is not
-
\(x \lt 5\quad\text{or}\quad x \geq 8 \qquad x = 8\)
The given value
is
is not
-
\(x \geq -1\quad\text{and}\quad x \leq 6 \qquad x = 6\)
The given value
is
is not
-
\(-1 \leq x \leq 1 \qquad x = -3\)
The given value
is
is not
Compound Inequalities and Interval Notation
15.
Solve the compound inequality. Write the solution set in interval notation.
\(\displaystyle{-3 \lt x \leq 1}\)
16.
Solve the compound inequality. Write the solution set in interval notation.
\(\displaystyle{-1 \lt x \leq 8}\)
17.
Solve the compound inequality. Write the solution set in interval notation.
\(\displaystyle{-10 > x\text{ or } x \geq 4}\)
18.
Solve the compound inequality. Write the solution set in interval notation.
\(\displaystyle{-9 > x\text{ or } x \geq 1}\)
19.
Express the following inequality using interval notation.
\(\displaystyle{x \lt -8 \text{ or } x \leq 7}\)
20.
Express the following inequality using interval notation.
\(\displaystyle{x \lt -7 \text{ or } x \leq 4}\)
21.
Express the following inequality using interval notation.
\(\displaystyle{-6 \lt x \text{ and } x\geq 10}\)
22.
Express the following inequality using interval notation.
\(\displaystyle{-5 \lt x \text{ and } x\geq 7}\)
23.
Express the following inequality using interval notation.
\(\displaystyle{-4 \leq x\text{ and } x \lt 3}\)
24.
Express the following inequality using interval notation.
\(\displaystyle{-3 \leq x\text{ and } x \lt 10}\)
Solving a Compound Inequality Algebraically
25.
Solve the compound inequality algebraically.
\(\displaystyle{-18 \lt 12 - x \leq -13}\)
26.
Solve the compound inequality algebraically.
\(\displaystyle{-1 \lt 5 - x \leq 4}\)
27.
Solve the compound inequality algebraically.
\(\displaystyle{3 \leq x+18 \lt 8}\)
28.
Solve the compound inequality algebraically.
\(\displaystyle{5 \leq x+11 \lt 10}\)
29.
Solve the compound inequality algebraically.
\(\displaystyle{ 11 \le \frac{5}{9}(F-32) \le 34 }\)
\(F\) is in
30.
Solve the compound inequality algebraically.
\(\displaystyle{ 14 \le \frac{5}{9}(F-32) \le 47 }\)
\(F\) is in
31.
Solve the compound inequality algebraically.
\(\displaystyle{-4x+5>9 \quad \text{or} \quad -18x-7\leq-5}\)
32.
Solve the compound inequality algebraically.
\(\displaystyle{-15x-2>18 \quad \text{or} \quad -20x+3\lt 15}\)
33.
Solve the compound inequality algebraically.
\(\displaystyle{3x-17>17 \quad \text{or} \quad -19x-13\geq12}\)
34.
Solve the compound inequality algebraically.
\(\displaystyle{-2x-19>19 \quad \text{or} \quad 11x+9\geq11}\)
35.
Solve the compound inequality algebraically.
\(\displaystyle{-x-6\leq16 \quad \text{and} \quad -15x-5\geq7}\)
36.
Solve the compound inequality algebraically.
\(\displaystyle{10x+15>-4 \quad \text{and} \quad 11x+16>3}\)
37.
Solve the compound inequality algebraically.
\(\displaystyle{-4x-9>-15 \quad \text{and} \quad -9x+20\geq20}\)
38.
Solve the compound inequality algebraically.
\(\displaystyle{-18x+9>14 \quad \text{and} \quad 11x-17\lt -5}\)
39.
Solve the compound inequality algebraically.
\({6} \lt \frac{2 }{7 }x \lt {16}\)
40.
Solve the compound inequality algebraically.
\({6} \lt \frac{3 }{7 }x \lt {21}\)
41.
Solve the compound inequality algebraically.
\({22} \gt -3 - \frac{5 }{2 }x \geq {-18}\)
42.
Solve the compound inequality algebraically.
\({9} \gt -1 - \frac{5 }{6 }x \geq {-21}\)
43.
Solve the compound inequality algebraically.
\(\displaystyle{ {18} \gt 3-\frac{5}{4}x \geq {-12} }\)
In set-builder notation, the solution set is .
In interval notation, the solution set is .
44.
Solve the compound inequality algebraically.
\(\displaystyle{ {-9} \gt -1-\frac{2}{3}x \geq {-11} }\)
In set-builder notation, the solution set is .
In interval notation, the solution set is .
Applications
45.
As dry air moves upward, it expands. In so doing, it cools at a rate of about \(1^{\circ}\text{C}\) for every \(100\,\text{m}\) rise, up to about \(12\,\text{km}\text{.}\)
If the ground temperature is \(16^{\circ}\text{C}\text{,}\) write a formula for the temperature at height \(x\,\text{km}\text{.}\) \(T(x)=\)
-
What range of temperature will a plane be exposed to if it takes off and reaches a maximum height of \(8\,\text{km}\text{?}\) Write answer in interval notation.
The range is .
