ORCCA Variables, Expressions, and Equations Chapter Review

Section 2.10 Variables, Expressions, and Equations Chapter Review

Subsection 2.10.1 Variables and Evaluating Expressions

In Section 2.1 we covered the definitions of variables and expressions, and how to evaluate an expression with a particular number. We learned the formulas for perimeter and area of rectangles, triangles, and circles.

Evaluating Expressions.

When we evaluate an expression's value, we substitute each variable with its given value.

Example 2.10.1.

Evaluate the value of $\frac{5}{9}(F - 32)$ if $F=212\text{.}$

\begin{align*} \frac{5}{9}(F - 32)\amp=\frac{5}{9}(212 - 32)\\ \amp=\frac{5}{9}(180)\\ \amp=100 \end{align*}

Substituting a Negative Number.

When we substitute a variable with a negative number, it's important to use parentheses around the number.

Example 2.10.2.

Evaluate the following expressions if $x=-3\text{.}$

$\displaystyle \begin{aligned}[t] x^2\amp=(-3)^2\\ \amp=9 \end{aligned}$
$\displaystyle \begin{aligned}[t] x^3\amp=(-3)^3\\ \amp=(-3)(-3)(-3)\\ \amp=-27 \end{aligned}$
$\displaystyle \begin{aligned}[t] -x^2\amp=-(-3)^2\\ \amp=-9 \end{aligned}$
$\displaystyle \begin{aligned}[t] -x^3\amp=-(-3)^3\\ \amp=-(-27)\\ \amp=27 \end{aligned}$

Subsection 2.10.2 Geometry Formulas

In Section 2.2 we established the following formulas.

Perimeter of a Rectangle: $\displaystyle P=2(\ell+w)$
Area of a Rectangle: $\displaystyle A=\ell w$
Area of a Triangle: $\displaystyle A=\frac{1}{2}bh$
Circumference of a Circle: $\displaystyle c=2\pi r$
Area of a Circle: $\displaystyle A=\pi r^2$
Volume of a Rectangular Prism: $\displaystyle V=wdh$
Volume of a Cylinder: $\displaystyle V=\pi r^2h$
Volume of a Rectangular Prism or Cylinder: $\displaystyle V=Bh$

Subsection 2.10.3 Combining Like Terms

In Section 2.3 we covered the definitions of a term and how to combine like terms.

Example 2.10.3.

List the terms in the expression $5x-3y+\frac{2w}{3}\text{.}$

Explanation

The expression has three terms that are being added, $5x\text{,}$ $-3y$ and $\frac{2w}{3}\text{.}$

Example 2.10.4.

Simplify the expression $5x-3x^2+2x+5x^2\text{,}$ if possible, by combining like terms.

Explanation

This expression has four terms: $5x\text{,}$ $-3x^2\text{,}$ $2x\text{,}$ and $5x^2\text{.}$ Both $5x$ and $2x$ are like terms; also $-3x^2$ and $5x^2$ are like terms. When we combine like terms, we get:

\begin{equation*} 5x-3x^2+2x+5x^2=7x+2x^2 \end{equation*}

Note that we cannot combine $7x$ and $2x^2$ because $x$ and $x^2$ represent different quantities.

Subsection 2.10.4 Equations and Inequalities as True/False Statements

In Section 2.4 we covered the definitions of an equation and an inequality, as well as how to verify if a particular number is a solution to them.

Checking Possible Solutions.

Given an equation or an inequality (with one variable), checking if some particular number is a solution is just a matter of replacing the value of the variable with the specified number and determining if the resulting equation/inequality is true or false. This may involve some amount of arithmetic simplification.

Example 2.10.5.

Is $-5$ a solution to $2(x+3)-2=4-x\text{?}$

Explanation

To find out, substitute in $-5$ for $x$ and see what happens.

\begin{align*} 2(x+3)-2\amp=4-x\\ 2(\substitute{(-5)}+3)-2\amp\stackrel{?}{=}4-\substitute{(-5)}\\ 2(\highlight{-2})-2\amp\stackrel{?}{=}\highlight{9}\\ \highlight{-4}-2\amp\stackrel{?}{=}9\\ \highlight{-6}\amp\stackrel{\text{no}}{=}9 \end{align*}

So no, $-5$ is not a solution to $2(x+3)-2=4-x\text{.}$

Subsection 2.10.5 Solving One-Step Equations

In Section 2.5 we covered to to add, subtract, multiply, or divide on both sides of an equation to isolate the variable, summarized in Fact 2.5.11. We also learned how to state our answer, either as a solution or a solution set. Last we discussed how to solve equations with fractions.

Solving One-Step Equations.

When we solve linear equations, we use Fact 2.5.11 and follow an algorithm to solve a linear equation.

Example 2.10.6.

Solve for $g$ in $\frac{1}{2}=\frac{2}{3}+g\text{.}$

Explanation

We will subtract $\frac{2}{3}$ on both sides of the equation:

\begin{align*} \frac{1}{2}\amp=\frac{2}{3}+g\\ \frac{1}{2}\subtractright{\frac{2}{3}}\amp=\frac{2}{3}+g\subtractright{\frac{2}{3}}\\ \frac{3}{6}-\frac{4}{6}\amp=g\\ -\frac{1}{6}\amp=g \end{align*}

We will check the solution by substituting $g$ in the original equation with $-\frac{1}{6}\text{:}$

\begin{align*} \frac{1}{2}\amp=\frac{2}{3}+g\\ \frac{1}{2}\amp\stackrel{?}{=}\frac{2}{3}+\left(\substitute{-\frac{1}{6}}\right)\\ \frac{1}{2}\amp\stackrel{?}{=}\frac{4}{6}+\left(-\frac{1}{6}\right)\\ \frac{1}{2}\amp\stackrel{?}{=}\frac{3}{6}\\ \frac{1}{2}\amp\stackrel{\checkmark}{=}\frac{1}{2} \end{align*}

The solution $-\frac{1}{6}$ is checked and the solution set is $\left\{-\frac{1}{6}\right\}\text{.}$

Subsection 2.10.6 Solving One-Step Inequalities

In Section 2.6 we covered how solving inequalities is very much like how we solve equations, except that if we multiply or divide by a negative we switch the inequality sign.

Solving One-Step Inequalities.

When we solve linear inequalities, we also use Fact 2.5.11 with one small complication: When we multiply or divide by the same negative number on both sides of an inequality, the direction of the inequality sign reverses!

Example 2.10.7.

Solve the inequality $-2x\geq12\text{.}$ State the solution set with both interval notation and set-builder notation.

Explanation

To solve this inequality, we will divide each side by $-2\text{:}$

\begin{align*} -2x\amp\geq12\\ \divideunder{-2x}{-2}\amp\highlight{{}\leq{}}\divideunder{12}{-2}\amp\amp\text{Note the change in direction.}\\ x\amp\leq-6 \end{align*}

The inequality's solution set in interval notation is $(-\infty,-6]\text{.}$
The inequality's solution set in set-builder notation is $\{x\mid x\leq-6\}\text{.}$

Subsection 2.10.7 Percentages

In Section 2.7 we covered how to translate sentences with percentages into equations that we can solve.

Solving One-Step Equations Involving Percentages.

An important skill for solving percent-related problems is to boil down a complicated word problem into a simple form like “$2$ is $50\%$ of $4\text{.}$”

Example 2.10.8.

What percent of $2346.19$ is $1995.98\text{?}$

Using $P$ to represent the unknown quantity, we write and solve the equation:

\begin{align*} \overbrace{\strut P}^{\text{what percent}}\overbrace{\strut \cdot}^{\text{of}} \overbrace{\strut 2346.19}^{\text{\$2346.19}}\amp\overbrace{\strut =}^{\text{is}}\overbrace{\strut 1995.98}^{\text{\$1995.98}}\\ \divideunder{P\cdot 2346.19}{2346.19}\amp=\divideunder{1995.98}{2346.19}\\ P\amp=0.85073\ldots\\ P\amp\approx85.07\% \end{align*}

In summary, $1995.98$ is approximately $85.07\%$ of $2346.19\text{.}$

Subsection 2.10.8 Modeling with Equations and Inequalities

In Section 2.8 we covered how to translate phrases into mathematics, and how to set up equations and inequalities for application models.

Modeling with Equations and Inequalities.

To set up an equation modeling a real world scenario, the first thing we need to do is identify what variable we will use. The variable we use will be determined by whatever is unknown in our problem statement. Once we've identified and defined our variable, we'll use the numerical information provided in the equation to set up our equation.

Examples.

A bathtub contains 2.5 ft³ of water. More water is being poured in at a rate of 1.75 ft³ per minute. When will the amount of water in the bathtub reach 6.25 ft³?

Since the question being asked in this problem starts with “when,” we immediately know that the unknown is time. As the volume of water in the tub is measured in ft³ per minute, we know that time needs to be measured in minutes. We'll define $t$ to be the number of minutes that water is poured into the tub. Since each minute there are 1.75 ft³ of water added, we will add the expression $1.75t$ to $2.5$ to obtain the total amount of water. Thus, the equation we set up is:

\begin{equation*} 2.5+1.75t=6.25 \end{equation*}

Subsection 2.10.9 Simplifying Expressions

In Section 2.9 we covered the definitions of the identities and inverses, and the various algebraic properties. We then learned about the order of operations.

Example 2.10.9.

Use the associative, commutative, and distributive properties to simplify the expression $5x+9(-2x+3)$ as much as possible.

Explanation

We will remove parentheses by the distributive property and then combine like terms:

\begin{align*} 5x+9(-2x+3)\amp=5x+9(-2x+3)\\ \amp=5x+9(-2x)+9(3)\\ \amp=5x-18x+27\\ \amp=-13x+27 \end{align*}

Exercises 2.10.10 Exercises

1.

A trapezoid’s area can be calculated by the formula $A=\frac{1}{2}(b_1+b_2)h\text{,}$ where $A$ stands for area, $b_1$ for the first base’s length, $b_2$ for the second base’s length, and $h$ for height.

Find the area of the trapezoid below.

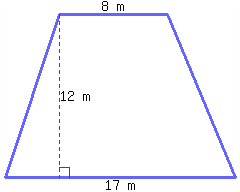
2.

Find the area of the trapezoid below.

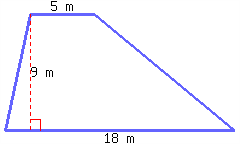
3.

To convert a temperature measured in degrees Fahrenheit to degrees Celsius, there is a formula:

\begin{equation*} C={\frac{5}{9}\!\left(F-32\right)} \end{equation*}

where $C$ represents the temperature in degrees Celsius and $F$ represents the temperature in degrees Fahrenheit.

If a temperature is $122 {^\circ}\text{F}\text{,}$ what is that temperature measured in Celsius?

4.

To convert a temperature measured in degrees Fahrenheit to degrees Celsius, there is a formula:

\begin{equation*} C={\frac{5}{9}\!\left(F-32\right)} \end{equation*}

where $C$ represents the temperature in degrees Celsius and $F$ represents the temperature in degrees Fahrenheit.

If a temperature is $14 {^\circ}\text{F}\text{,}$ what is that temperature measured in Celsius?

5.

Evaluate the expression ${x^{2}}\text{:}$

For $x=2\text{.}$
For $x=-6\text{.}$

6.

Evaluate the expression ${y^{2}}\text{:}$

For $y=7\text{.}$
For $y=-9\text{.}$

7.

Evaluate the expression ${y^{3}}\text{:}$

For $y=3\text{.}$
For $y=-3\text{.}$

8.

Evaluate the expression ${r^{3}}\text{:}$

For $r=5\text{.}$
For $r=-5\text{.}$

9.

List the terms in each expression.

${8y+8x+7s}$
${-3y^{2}-7x^{2}-5t^{2}}$
${6x-s}$
${-3x}$

10.

List the terms in each expression.

${-9y^{2}-3z^{2}+5z-4y}$
${7t+7y}$
${y^{2}-7+9t}$
${3s+3+4x^{2}-8z^{2}}$

11.

Simplify each expression, if possible, by combining like terms.

${-8y+6s+3s-5s^{2}}$
${3y+t^{2}+y^{2}+3y^{2}}$
${-6y^{2}-7z^{2}}$
${-z^{2}-7z^{2}+2z^{2}}$

12.

Simplify each expression, if possible, by combining like terms.

${-6y^{2}-5x-2z^{2}+6x^{2}}$
${-2s+5s-8s}$
${7y+2y}$
${7y^{2}-6z}$

13.

Simplify each expression, if possible, by combining like terms.

${-{\frac{4}{5}}y+{\frac{1}{3}}t}$
${{\frac{7}{8}}z - {\frac{5}{8}}x}$
${t^{2}+{\frac{3}{2}}t^{2}-t^{2} - {\frac{3}{2}}z^{2}}$
${-{\frac{1}{2}}y^{2}+{\frac{3}{4}}y}$

14.

Simplify each expression, if possible, by combining like terms.

${{\frac{1}{3}}y^{2}+{\frac{3}{2}}y^{2}}$
${-{\frac{5}{9}}y - {\frac{9}{5}}s+{\frac{1}{6}}s+{\frac{1}{4}}t^{2}}$
${-8x+{\frac{3}{4}}t^{2}}$
${-{\frac{2}{9}}s+s+{\frac{7}{3}}s^{2}+s^{2}}$

15.

Is $-2$ a solution for $x$ in the equation ${4x+2}={1-\left(9+x\right)}\text{?}$ Evaluating the left and right sides gives:

${4x+2}$	$=$	${1-\left(9+x\right)}$
	${}\stackrel{?}{=}{}$

So $-2$

is
is not

a solution to ${4x+2}={1-\left(9+x\right)}\text{.}$

16.

Is $-1$ a solution for $x$ in the equation ${2x-4}={-2-\left(5+x\right)}\text{?}$ Evaluating the left and right sides gives:

${2x-4}$	$=$	${-2-\left(5+x\right)}$
	${}\stackrel{?}{=}{}$

So $-1$

is
is not

a solution to ${2x-4}={-2-\left(5+x\right)}\text{.}$

17.

Is $4$ a solution for $x$ in the inequality ${-3x^{2}+5x}\le{-4x-5}\text{?}$ Evaluating the left and right sides gives:

${-3x^{2}+5x}$	$\le$	${-4x-5}$
	${}\stackrel{?}{\le}{}$

So $4$

is
is not

a solution to ${-3x^{2}+5x}\le{-4x-5}\text{.}$

18.

Is $2$ a solution for $x$ in the inequality ${-4x^{2}+5x}\le{2x}\text{?}$ Evaluating the left and right sides gives:

${-4x^{2}+5x}$	$\le$	${2x}$
	${}\stackrel{?}{\le}{}$

So $2$

is
is not

a solution to ${-4x^{2}+5x}\le{2x}\text{.}$

19.

Solve the equation.

$\displaystyle{ {t+2}={-5} }$

20.

Solve the equation.

$\displaystyle{ {t+8}={5} }$

21.

Solve the equation.

$\displaystyle{ {-12}={t-8} }$

22.

Solve the equation.

$\displaystyle{ {-12}={x-10} }$

23.

Solve the equation.

$\displaystyle{ {60}={-5x} }$

24.

Solve the equation.

$\displaystyle{ {49}={-7y} }$

25.

Solve the equation.

$\displaystyle{ {{\frac{3}{13}}b}={15} }$

26.

Solve the equation.

$\displaystyle{ {{\frac{6}{11}}A}={12} }$

For each problem below, in addition to writing the different notations for each solution set, draw a graph of each solution set on a number line.

Solve each inequality.

27.

${x+4} > {7}$

28.

${x-4} \leq {6}$

29.

${5} \leq {x+9}$

30.

${5} > {x-7}$

31.

${2x} \leq {8}$

32.

${7x} > {2}$

33.

${-3x} \geq {6}$

34.

${12} \geq {-3x}$

35.

${6} \lt {-x}$

36.

${-x} \leq {7}$

37.

${-32} \lt {{\frac{8}{9}}x}$

38.

${5x} > {-15}$

39.

The pie chart represents a collector’s collection of signatures from various artists.

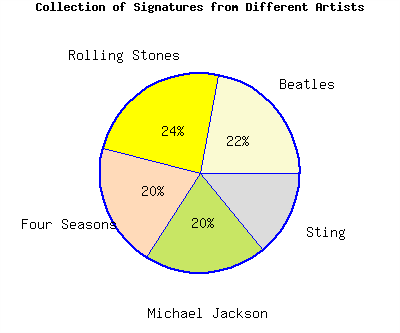
If the collector has a total of $1950$ signatures, there are signatures by Sting.

40.

The pie chart represents a collector’s collection of signatures from various artists.

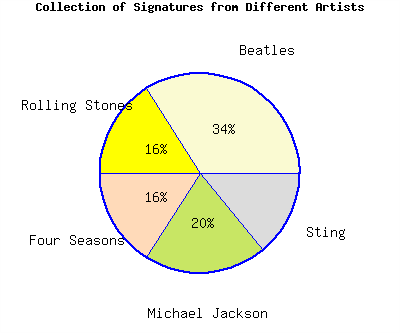
If the collector has a total of $450$ signatures, there are signatures by Sting.

41.

A community college conducted a survey about the number of students riding each bus line available. The following bar graph is the result of the survey.

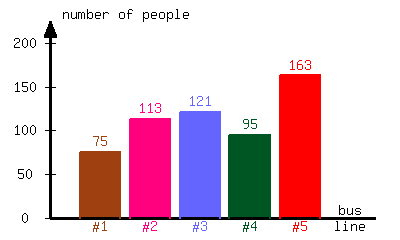
What percent of students ride Bus #1?

Approximately of students ride Bus #1.

42.

A community college conducted a survey about the number of students riding each bus line available. The following bar graph is the result of the survey.

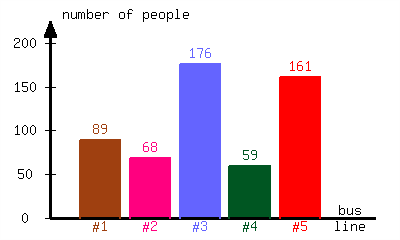
What percent of students ride Bus #1?

Approximately of students ride Bus #1.

43.

The following is a nutrition fact label from a certain macaroni and cheese box.

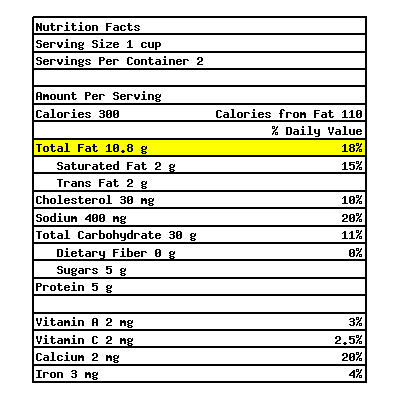
The highlighted row means each serving of macaroni and cheese in this box contains ${10.8\ {\rm g}}$ of fat, which is $18\%$ of an average person’s daily intake of fat. What’s the recommended daily intake of fat for an average person?

The recommended daily intake of fat for an average person is .

44.

The following is a nutrition fact label from a certain macaroni and cheese box.

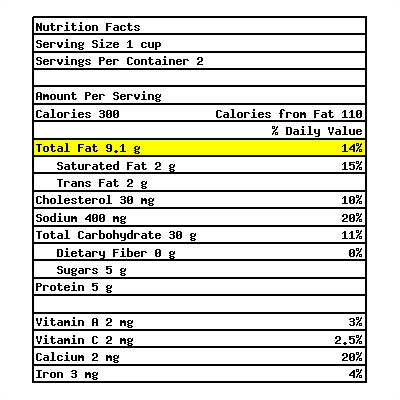
The highlighted row means each serving of macaroni and cheese in this box contains ${9.1\ {\rm g}}$ of fat, which is $14\%$ of an average person’s daily intake of fat. What’s the recommended daily intake of fat for an average person?

The recommended daily intake of fat for an average person is .

45.

Dave used to make $16$ dollars per hour. After he earned his Bachelor’s degree, his pay rate increased to $53$ dollars per hour. What is the percentage increase in Dave’s salary?

The percentage increase is .

46.

Tracei used to make $17$ dollars per hour. After she earned her Bachelor’s degree, her pay rate increased to $60$ dollars per hour. What is the percentage increase in Tracei’s salary?

The percentage increase is .

47.

This line graph shows a certain stock's price change over a few days.

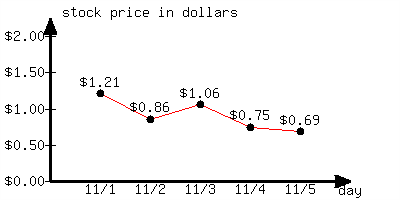
From 11/1 to 11/5, what is the stock price’s percentage change?

From 11/1 to 11/5, the stock price’s percentage change was approximately .

48.

This line graph shows a certain stock's price change over a few days.

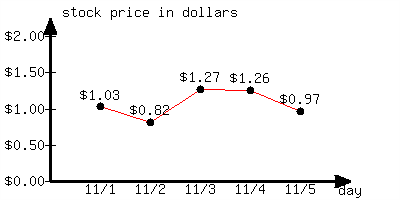
From 11/1 to 11/5, what is the stock price’s percentage change?

From 11/1 to 11/5, the stock price’s percentage change was approximately .

49.

A house was bought two years ago at the price of ${\$380{,}000}\text{.}$ Each year, the house’s value decreased by $2\%\text{.}$ What’s the house’s value this year?

The house’s value this year is .

50.

A house was bought two years ago at the price of ${\$240{,}000}\text{.}$ Each year, the house’s value decreased by $3\%\text{.}$ What’s the house’s value this year?

The house’s value this year is .

51.

A bicycle for sale costs ${\$126.00}\text{,}$ which includes $5\%$ sales tax. What was the cost before sales tax?

Assume the bicycle’s price before sales tax is $p$ dollars. Write an equation to model this scenario. There is no need to solve it.

52.

A bicycle for sale costs ${\$160.50}\text{,}$ which includes $7\%$ sales tax. What was the cost before sales tax?

Assume the bicycle’s price before sales tax is $p$ dollars. Write an equation to model this scenario. There is no need to solve it.

53.

A wading pool is being filled with water from a garden hose at a rate of $6$ gallons per minute. If the pool already contains $60$ gallons of water and can hold up to $186$ gallons, set up an inequality modeling how much time can pass without the pool overflowing. There is no need to solve it.

54.

A wading pool is being filled with water from a garden hose at a rate of $10$ gallons per minute. If the pool already contains $70$ gallons of water and can hold up to $370$ gallons, set up an inequality modeling how much time can pass without the pool overflowing. There is no need to solve it.